极C－invex条件下多目标分式规划问题的对称对偶性

金爱莲

（延边大学理学院 数学系，吉林 延吉133002）

极C－invex条件下多目标分式规划问题的对称对偶性

金爱莲

（延边大学理学院 数学系，吉林 延吉133002）

给出了多目标分式规划问题，并利用弱有效性和真有效性的概念，证明了在极C－invex条件下与分式规划问题相关的弱对偶定理、强对偶定理和逆对偶定理.

极C－invex；多目标分式规划；对称对偶性；有效性

多目标规划研究的是一定约束条件下的多个目标函数的极值问题，是近年发展起来的数学规划的新分支，应用广泛.近几年来，有关函数的极C－invex的研究也引起了诸多学者的兴趣.Dantzig［1］等于1965年首先提出了非线性规划问题的对称对偶性，随后许多学者对此问题做过进一步的研究，但其结果大都是在凸性或广义凸性上得到的［2－5］.杨新民［6］讨论并证明了在不变伪凸性条件下两类非线性规划的对称对偶性，陈秀宏［7］讨论了锥约束多目标规划的二阶对称对偶性，金爱莲［8］讨论了极C－invex条件下多目标非线性规划问题的对称对偶性.本文在文献［8］和［9］的研究基础上，证明了极C－invex条件下多目标分式规划问题的弱对偶定理、强对偶定理和逆对偶定理.

1 预备知识

设Rp是p 维欧氏空间，记Rp＋＝ ｛x∈Rp｜x≧0｝，Rp－＝ ｛x∈Rp｜x≦0｝.设x，y∈Rp，若对所有的i＝1，2，…，p，有xi≤yi，则记为x≦y；若x≦y且x≠y，则记为x≤y；若对所有的i＝1，2，…，p，有xi＜yi，则记为x＜y；若对x≤y的否定，则记为xy.

定义1 称非空集C⊆Rp是1个顶点为零的锥，若x∈C，则对所有λ≥0，有λx∈C.如果C又

其中fi，gi∶C→C1，h∶C→C2，C，C1和C2分别是Rp，Rn和Rm中具有非空的闭凸锥.设X＝ ｛x∈C｜h（x）≦0｝是所有（MP）的可行解的集合.

定义4 称1个锥C＋是C的正极锥，若C＋＝｛p∈Rp｜pTx≧0，∀x∈C｝.

定义5 设f＝（f1，f2，…，fp）∶C1→C是可微函数，且C1⊆Rn和C⊆Rp是非空的闭凸锥，称f是关于η∶C1×C1→C1的C1上的极C－invex，如果对所有λ（≠0）∈C＋和所有（x，u）∈C1×C1有（λTf）（x）－（λTf）（u）≧［η（x，u）］T∇x（λTf）（u），即对所有λ∈C＋，λ≠0，实值函数fλ（x）＝λTf（x）是凸的（invex）.是凸的，则称C是1个凸锥，特别地，当C为闭集时，则称C为闭凸锥.考虑下面的多目标分式规划问题：

2 主要结果及其证明

设C，C1和C2为闭凸锥，S1⊆Rn和S2⊆Rm是开的，且A＝S1⊆Rn，B＝S2⊆Rm.C1⊂A，C2⊂B，f∶A→C⊆Rp，g∶B→C⊆Rp是2个可微函数.对于i＝1，2，…，p，假设f和－g是对于x的关于η在C1上的极C－invex，－f和g是对于y的关于ξ在C2上的极C－invex.在可行区域，始终假设fi＞0，i＝1，2，…，p，且每个gi是有界的.注意η∶S1×S1→C1和ξ∶S2×S2→C2.

为了简化，（FSP）和（FSD）可重新表示如下：

下面给出关于（FSP）′和（FSD）′的弱、强和逆对偶定理，这些结果同样适用于（FSP）和（FSD）问题．

定理1 （弱对偶性）设（x，y，λ）是（FSP）′的可行解，（u，v，λ）是（FSD）′的可行解．假设f和－g是关于x的极C－invex，－f和g是关于y的极C－invex，并且η（x，u）＋u∈C1，ξ（v，y）＋y∈C2，则qp．

证明 由（3）式及（fi－pigi）是极C－invex的假设，有．由η（x，u）＋u∈C1和（5）式有．再由（4）式得到

同样，由－（fi－qigi）是极C－invex的条件，得到，并由ξ（v，y）＋y ∈C2和（2）式得到．再由（1）式得到

由（6）和（7）式得到

如果对某个i，qi＞pi，且对所有j≠i，qj≦pj，则因为gi＞0，i＝1，2，…，p，我们可以得到1个与（8）式相矛盾的结论，因此qp．由此定理1得证．

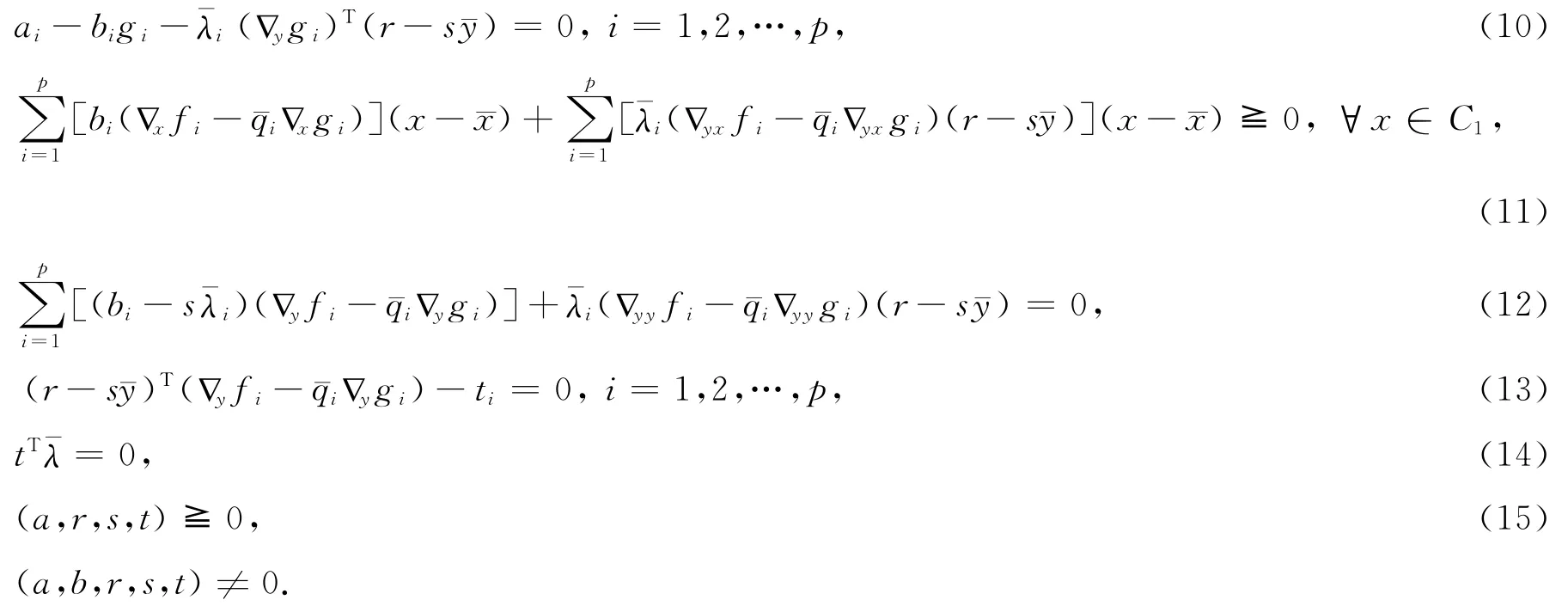
因为λ∈C＋，t≧0，由（14）式容易得到t＝0．因此由（13）式可得

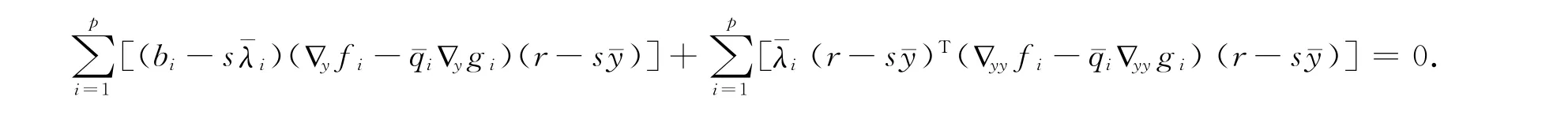
因为x∈C1，∈C1，C1又是闭凸锥，故可知x＋∈C1，因此由（18）式得由此推出同样在（18）式中，令x＝0，x＝2，得0．因此,,）是（FSD）′的可行解，且（FSP）′和（FSD）′的目标值相等．显然（，，）是（FSD）′的有效解．如果（,，）是非真有效的，则对某个可行解（ui，vi，），满足p1i＝fi（ui，vi）／gi（ui，vi），i＝1，2，

…，p，且对某个i，对任意M＞0，有p1i－＞M，又因为gi（i＝1，2，…，p）是有界的，因此p1i）gi，vi）＜0，这与弱对偶性的不等式（8）发生矛盾，因此（，，）是（FSD）′的真有效解．定理2得证．

同样可以得到逆对偶定理，其证明过程类似于定理2，故省略．

［1］ Dantzig G B，Eisenberg E，Cottle R W．Symmetric dual nonlinear programs［J］．Pacific J Math，1965，15：809－812．

［2］ Mond B，Weir T．Symmetric duality for nonlinear multiobjective programming［C］／／S Kumar Recent Developments in Mathematical Programming．London：Gordon and Breach，1997：137－153．

［3］ Bazaraa MS，Goode J J．On symmetric duality in nonlinear programming［J］．Operation Research，1973，21：1－9．

［4］ Chandra S，Craven B D，Mond B．Symmetric dual fractional programming［J］．Z Oper Res，1984，29：59－64．

［5］ 刘三阳．分式规划的对称对偶性［J］．西安交通大学学报，1990，24：135－138．

［6］ 杨新民．两类非线性规划的对称对偶性［J］．重庆师范学院学报，1993，10：5－8．

［7］ 陈秀宏．锥约束多目标规划的二阶对称对偶性质［J］．应用数学，2006，19：127－133．

［8］ 金爱莲．极C－invex条件下多目标非线性规划问题的对称对偶性［J］．延边大学学报：自然科学版，2010，36（4）：291－295．

［9］ Kim D S，Yun Y B，Lee W J．Multiobjective symmetric duality with cone constraints［J］．European Journal of Operational Research，1998，107：686－691．

Symmetric duality for multiobjective fractional programming problem with polarlyC－invexity

JIN Ai－lian
（DepartmentofMathematics，CollegeofScience，YanbianUniversity，Yanji133002，China）

A pair of multiobjective fractional programming with come constraints ws formulated and the definitions of a class of polarlyyC－invex fuctions were introduced.Under the polarlyC－invexity condition，we proved weak，strong and converse duality theorems by concept of the efficiency and the proper efficiency.

polarlyC－invex；multiobjective fractional problem；symmetric duality；efficiency

O212.2

A

1004－4353（2012）01－0033－05

2011－09－24

金爱莲!（1968—），女，讲师，研究方向为运筹学.