两两NQD阵列加权乘积和的完全收敛性

王宽程，杨英钟

（闽南理工学院 信息管理系，福建 泉州362700）

两两NQD阵列加权乘积和的完全收敛性

王宽程，杨英钟

（闽南理工学院 信息管理系，福建 泉州362700）

利用截尾和矩不等式方法，研究在h－可积条件下两两NQD阵列加权乘积和的完全收敛性，所得结果推广和改进了文献［7］中定理2.2的结论.

两两NQD阵列；h－可积；乘积和；完全收敛性

0 引言

两两NQD列是由统计学家Lehmann［1］提出的一类相当广泛的随机交量序列，著名的NA列［2］就是它的特殊情况之一.许多学者对两两NQD列极限理论进行了研究，并取得了一些成果.例如：王岳宝等［3］讨论了不同分布两两NQD列乘积和的强稳定性；陆凤彬［4］讨论了两两NQD列的完全收敛性和强大数定律；陈平炎［5］讨论了两两NQD列在满足r（1＜r＜2）阶Cesaro一致可积条件下的Lr收敛性；文献［6］提出了h－可积的概念并研究了随机变量序列加权和的平均收敛性.本文在上述研究的基础上，研究在h－可积条件下两两NQD阵列加权乘积和的完全收敛性，所得结果推广和改进了文献［7］中定理2.2的结论.

定义1 称X和Y是NQD的，若对∀x，y∈R，有P（X＜x，Y＜y）≤P（X＜x）P（Y＜y）；称r.v.序列｛Xn，n≥1｝是两两NQD的，若对 ∀i≠j，Xi和Xj是NQD的.

定义2 称随机变量阵列｛Xnk，1≤k≤n，n＞1｝是行两两NQD的，如果对任意的n≥2，有Xn1，Xn2，…，Xnn是两两NQD的.

定义3 设｛Xnk，un≤k≤vn，n≥1｝是随机变量阵列，｛ank，un≤k≤vn，n≥1｝是常数阵列，且.令｛h（n），n≥1｝是递增的正数列，且h（n）↑∞ （n→ ∞）.若其满足以下条件：

则称阵列｛Xnk｝关于常数阵列｛ank｝是h－可积的.

引理1［3］对任意实数列｛xi，i≥1｝及任意n≥m≥1有，其中是与n及｛xj，j≥1｝无关的常数.

引理2［8］设l（x）＞0为x→ ∞ 的缓变函数，则

引理3［9］设｛Xn，n≥1｝是两两 NQD列，EXn＝0，EX2n＜ ∞ （n≥1），记，其中j≥0，则有：

本文中恒设定N为正整数集，｛Xnk，1≤k≤n，n∈N｝是定义在同一概率空间的随机变量阵列.I（A）为A的示性函数.约定C表示正常数，且在不同地方表示不同的值.

1 主要结论及其证明

定理1 设｛Xnk，1≤k≤n，n≥1｝为零均值且方差有限的行两两NQD的阵列，｛ank，1≤k≤n，n≥1｝是常数阵列，｛h（n），n≥1｝是单调不减序列，且h（n）↑∞，n→ ∞，l（x）是缓变函数.设α＞0，αp＞1，0＜δ＜1，q＞0，t＞0为实数，满足αp－q＜0，ap－t＜0及α－q＋1＜0.若下面3个条件成立：① ｛Xnk｝是关于常数阵列ank的h－可积分；则对任意m∈N，有

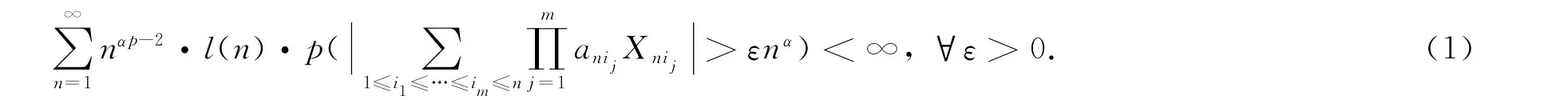
证明 由引理1及Jessen不等式知，证明（1）式，只须证明（2）和（3）式即可.

对每个1≤i≤n（n≥1），令Yni＝－h（n）I（Xni＜－h（n））＋XniI（｜Xni｜＜h（n））＋h（n）I（Xni＞h（n）），则｛Yni｝也为行两两NQD阵列，从而有，由此证明（2）式只需证明S1＜∞和S2＜∞.对于S2，由Chebyshev不等式及方差有界性，对2k≤n≤2k＋1，k∈N，根据条件③有.对于S1，由EXni＝0可得EXniI（｜Xni｜≤h（n））＝－EXniI（｜Xni｜＞h（n））.由条件 ① 有

根据（4）式，对充分大的n，由Chebyshev不等式和引理2、3及条件②，有

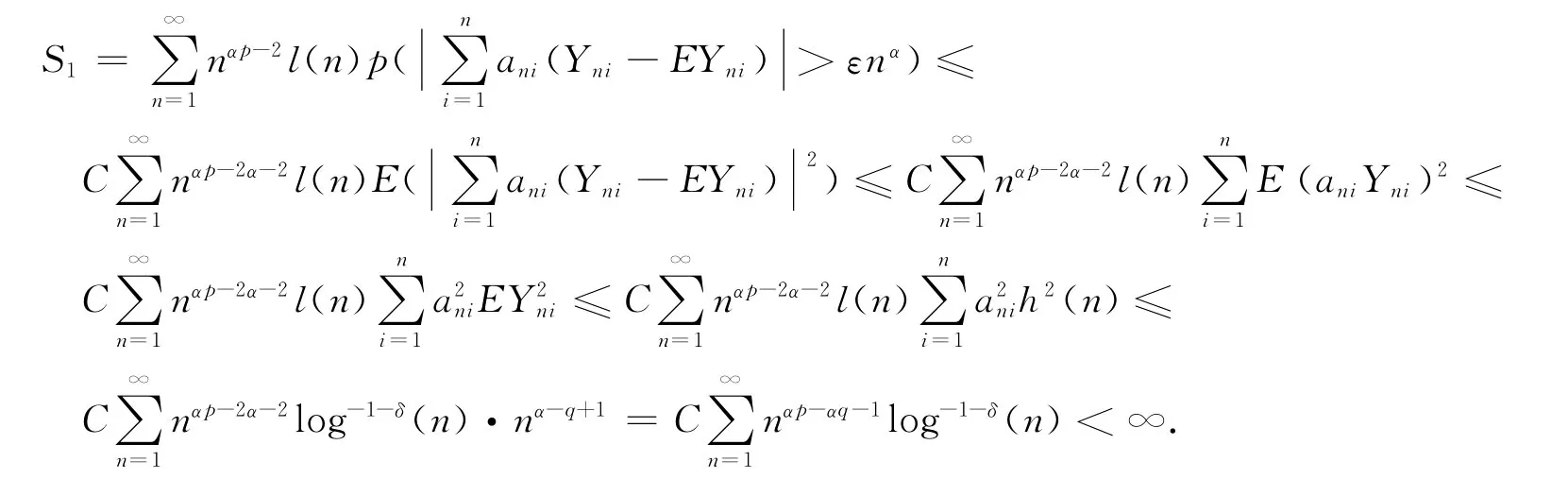
对于（3）式有

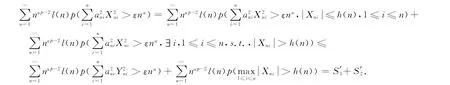
［1］Lehmann E L.Some concepts of dependence［J］.Ann Math Statist，1966，43：1137－1153.

［2］Joag－Dev K，Proschan F.Negative association of random variables with applications［J］.Ann Statist，1953，11：286－295.

［3］王岳宝，严继高，成凤，等.关于不同分布两两NQD列的Jamsion型加权乘积和的强稳定性［J］.数学年刊，2001，22A（6）：701－706.

［4］陆凤彬.两两 NQD序列的完全收敛性和强大数定律［J］.应用数学，2003，16（4）：29－33.

［5］陈平炎.两两 NQD随机序列的Lr收敛性［J］.数学物理学报，2008，28A（3）：447－453.

［6］Cabrera MO，Volodin A I.Mean convergence theorems and weak laws numbers for weighted sums of random variables under a condition of weighted integrability［J］.J Math Anal Appl，2005，305（2）：644－658.

［7］章茜，王文胜.h－可积条件下两两 NQD阵列加权和的完全收敛性［J］.吉林大学学报：理学版，2010，48（2）：183－188.

［8］Bingam N H，Goldie C M，Teugels J L.Regular Variation［M］.Cambridge：Cambridge University Press，1987.

［9］吴群英.两两 NQD列的收敛性质［J］.数学学报，2002，45（3）：617－624.

Complete convergence for the weighted product sums of pairwise NQD random arrays

WANG Kuan－cheng，YANG Ying－zhong
（DepartmentofInformationManagement，MinnanUniversityofScienceand Technology，Quanzhou362700，China）

Under the condition ofh－integrality，we investigate the complete convergence for the weighted sums of pairwise NQD random arrays using the means moment inequality and truncated method.The results extende and improve the results in［7］.

pairwise NQD random arrays；h－integrality；product sums；complete convergence

O211.4

A

1004－4353（2012）01－0025－03

2012－02－17

福建省教育厅科技项目（JB11215）

王宽程（1981—），男，讲师，研究方向为概率极限理论.