声速有限条件下的纯方位方法
李长文,赵建昕
(海军潜艇学院,山东 青岛 266042)
用纯方位方法对等速直航目标运动要素进行估计,是一个经典问题,其方法为观测站使用被动声纳观测声源发出的信号并给出声源的方位,然后利用一定的原理对目标运动要素进行估计或对其运动状态进行预测等。根据文献[1-4],传统作法一般不考虑声音在海水中传播的时间,即认为声速为无限值,可观测的目标方位即当前时刻噪声源的实际方位。考虑到声音在海水中传播总需要一定时间,对于运动目标,可被观测的目标方位并非目标噪声源当前时刻的实际方位,所观测的方位必与目标运动要素及声速有关,基于无误差条件下的这个关系,就可以研究纯方位条件下目标运动要素的估计问题。
声源发出的瞬时噪声经水声信道作用后,于观测站处所检测到的信号一般为一个非瞬时信号[5-6],因此由检测装置给出的观测到目标的时刻并非严格的声音沿特定途径到达观测站的时刻,所以自声源发出噪声信号至观测站检测到信号的时间延迟是由比较复杂的物理过程决定的,其所依赖的变量至少应包括声源深度、观测站深度、观测站到声源水平距离、水声环境等,不能简单地认为是声音沿直线匀速运动到观测站的,即不能人为地设想声音自声源传播至观测点的速度这一概念。因此本文所说的声音在海水中的传播速度,是指一个假想的平均速度Vs(t),即 t时刻到达观测站的声信号对应的声源至观测站的水平距离与信号发出至被检测到的延迟时间之比,对于t时刻所观测到的声音信号,将被认为以这个假想的平均速度于观测站所处水平面上自声源位置点处向外匀速直线运动。若不考虑声音信号自发出至被观测到的时间延迟,则相当于认为Vs(t)= ∞。
1 等速直航目标可被观测的方位真值β(t)的规律及运动要素的可观测性
假设目标作等速直航运动,以 V0、C0表示其速率与航向,以D0、β0表示 0时刻目标相对观测站的实际距离与方位真值,称(V0, C0, D0, β0)为等速直航目标的运动要素。
假设目标及观测站在同一水平面上运动,如图1,以0时刻观测站实际位置O 为原点,正北( N )方向为Ox 轴正方向,正东 ( E )方向为Oy 轴正方向,建立一个平面直角坐标系。角的符号符合标准数学教科书的规定,即自Ox轴旋转90 °至Oy轴的方向为正方向,此处与顺时针为正的航海习惯一致。为了表达式简洁,平面上的点、向量及其运算可以用复数表示,其中arg(z)表示复数z的[0, 2π)上的辐角主值,i 为虚数单位,Re(z),表示复数 z的实部,Im(z)表示复数 z的虚部。

图1 无误差的观测站A、目标B、可观测点 P 的位置图
以A(t)= xA(t)+ i yA(t)表示t时刻观测站实际位置,忽略观测站自身定位误差,则 A(t)对于观测者是确定的已知函数。t时刻目标实际位置点为

以 D0(t)= | A(t)B(t)|、β0(t)= arg(A(t)B(t))分别表示t时刻目标相对观测站实际距离及方位真值,其中A(t)B(t)= B(t)– A(t)。
以β(t)表示 t时刻所观测到的目标方位,对于Vs(t)< ∞的情形,β(t)非当前时刻目标的真实方位β0(t),而是目标于当前时刻之前的某个位置点 P(t)所发出的声音信号到达观测站的到达角(到达方向的反方向相对正北方向的角),即

其中 A(t)P(t)= P(t)– A(t),以下称β(t)为可被观测的方位真值。若认为 Vs(t)= ∞,则β(t)= β0(t)。
P(t)相当于 t 时刻可被观测到的声源位置点,记D(t)= | A(t)P(t)|,则声音自P(t)到达观测站的时间为D(t)/ Vs(t),因此

此方程应对应于唯一的(D(t), β(t)),下面研究其计算公式。由式(1)及式(3)可得

记 k(t)= V0/ Vs(t),则 0 ≤ k(t)<< 1,且
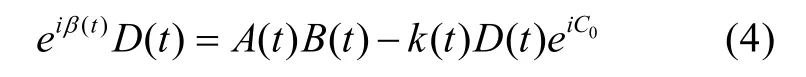
因此

计算后整理成关于D(t)的一元二次方程

其中 a(t)= 1 – k2(t)> 0,b(t)的计算公式为

因为 D(t)≥ 0,所以

由式(4)可得

这就是利用(t, V0, C0, D0, β0, Vs(t), A(t))计算 D(t)、β(t)的公式。
将式(4)改写为
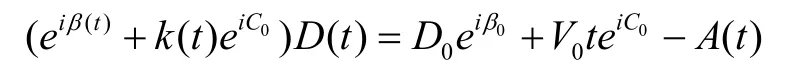
此式两端的实部与虚部之比对应的等式为

利用这一关系可以研究目标运动要素的可观测性。
若观测站静止,则xA(t)= yA(t)= 0,式(7)变为

对于Vs(t)为确定的已知函数的情形,若Vs(t)=∞,则 k(t)= 0,式(8)变为
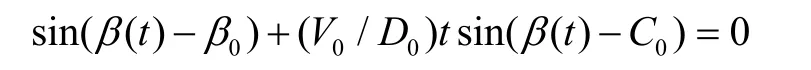
当 sin(β(t)– β0)不恒为 0,即观测站静止且不位于目标航向线上时,可观测的参数为(V0/ D0, C0, β0)而非(V0, C0, D0, β0)。当观测站机动时,基于式(7)(k(t)= 0),(V0, C0, D0, β0)是可观测的[4]。
设静止的观测站不位于目标航向线上,Vs(t)已知且Vs(t)∈ [V0, ∞ ),下面证明运动要素是可观测的,且只需 4个无误差方位即可唯一确定(V0, C0, D0,β0)。记 Z = (z1, …, z4)T,其中

则Z ≠ 0,且Z与目标运动要素相互唯一确定。令

利用这些记号,设 0 ≤ t1< t2< t3< t4,式(8)对应的方程组为


因为Z ≠ 0,不妨假设z4≠ 0,上述方程组依次相邻两式相减可得方程组

其中(以r 表示矩阵的行标,c 表示列标)

在观测站不位于目标航向线上的条件下,矩阵G一般非奇异,因此

其中 p = (p1, p2, p3)T= G–1q,将式(10)代入式(9)的第一个方程,可得

因为 z4≠ 0,所以

代入式(10)计算(z1, z2, z3),由此可得方程式(9)的唯一非零解,这个解对应唯一的目标运动要素:

下面用一个算例质疑以上结论,设V0= 15.4 kn,C0= 65.3°,D0= 100.2链,β0= 0.1°,A(t)= 0,(t1, t2, t3, t4)= (5, 6.6, 7.1, 9.9)s,Vs(t1, t2, t3, t4)= (1455, 1495, 1505,1499 )m/s,则以上计算项目为:

计算的 V0, C0, D0, β0与设定值误差均小于 10–7。
这些结论说明,考虑Vs(t)为确定的已知有限函数对应的纯方位条件下的目标运动要素的可观测性优于认为Vs(t)= ∞ 的情形。因此,可以期望相应的观测度应有同样的性质,即考虑观测误差条件下,对应于相同的观测站机动方式,Vs(t)< ∞ 对应的目标运动要素估计应优于认为Vs(t)= ∞ 的情形。
2 假设平均声速为常数的目标运动要素估计
平均声速 Vs(t)一般不为常数,只有在一定区域内可以看成常数,下面假设Vs(t)= Vs为一常数,对于Vs已知的情形 θ = (V0, C0, D0, β0)为纯方位观测条件下的待估计参数向量,其取值空间可定为Θ = [1,25]×[0, 2π )×[1852, 37040)×[0, 2 π )。对于 Vs未知的情形,待估计参数向量为θ = (V0, C0, D0, β0, Vs),其取值空间可定为Θ =[1, 25]×[0, 2π )×[1852, 37040)×[0, 2 π )× [1400, 1550]。
设 tn = (n – 1)Δt时刻β(tn )的观测值为βn,观测误 差 为 Δβ(tn),则 :Δβ(tn)=βn–β(tn),n=1,…,N 假 设Δβ(tn),n =1,…,N 为相互独立同 N(0,σβ2)分布的随机误差,其平方和为
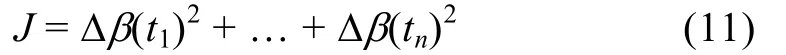
对于给定的Δt > 0,N,A(tn), n = 1, …, N,若 Vs已知,则 J为(V0, C0, D0, β0)的函数,若 Vs未知,则 J 为(V0,C0, D0, β0,Vs)的函数,下面只讨论这一情形。称J在Θ上的最小值点 ( V0*, C0*, D0*, β0*, Vs*)为( V0, C0, D0,β0, Vs)的非线性最小二乘法估计,这个估计应为方程组的解,下面研究这个估计的性质。
根据以上假设,(β1, …, βN)的似然函数为


这个方程组等价于

所以,( V0*, C0*, D0*, β0*, Vs*)为的极大似然估计,且σβ2的极大似然估计为
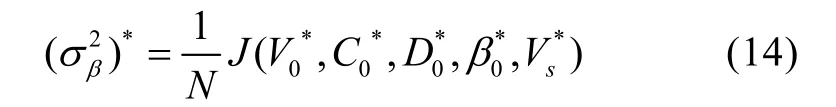
(σβ2)*并非σ2β的无偏估计,类似于标准的线性最小二乘法的性质,应将式(14)内的 N 改为N – 5,若Vs已知,则改为N – 4,数值实验发现,这个方法可以对σβ给出比较精确的估计。因为J( V0*, C0*, D0*, β0*,Vs*)为对应于估计值的剩余平方和,所以可以用σβ*检验计算的精度,σβ*与 σβ越接近,则观测值信息利用得越充分。
因为非线性最小二乘法估计的算法不如线性最小二乘法简单,除考虑计算的正确性、计算速度外,还必须考虑初值的稳定性。数值实验发现,计算 V0*,C0*, D0*, β0*, Vs*所需要的算法不太依赖于初值的选取。以区域 Θ 的中点作为搜索起点,可以给出比较精确的数值解。若有比较准确的目标运动要素的先验知识,则人工输入初值,可以加快计算速度。
假设已给出( V0*, C0*, D0*, β0*),则可以对任一时刻t目标实际距离D0(t),方位β0(t)进行估计,其公式为
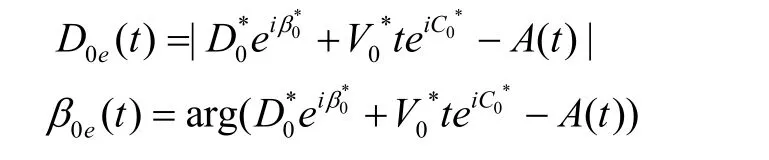
3 运动要素估计的经典方法
若认为 Vs= ∞,则 k(t)= 0,式(7)变为

记 X = (tnsinβn, – tncosβn, sinβn, – cosβn)N×4Y =(xA(tn)sinβn– yA(tn)cosβn)N×1,则无误差条件下 Y = XZ,在有观测误差的条件下,Y – XZ 的各分量并非相互独立同分布的,且X 与方位观测值有关,所以Y 与Z并非满足严格线性拟合模型,但在观测站机动的条件下,还是可以计算 min || Y – X Z ||2的解

Z*对应的目标运动要素估计用(V0l, C0l, D0l, β0l)表示,以下称之为线性估计,这就是不考虑观测信号时间延迟条件下,估计目标运动要素的传统方法。即使观测站机动,XTX 亦可能表现出近似奇异性,实验程序内用伪逆 pinv( XTX )代替( XTX )–1。计算(V0l, C0l,D0l, β0l)的作用之一是作为非线性算法(V0, C0, D0,β0)的初值,数值实验发现,这个初值对于加快计算速度有时是十分有效的。
4 给定观测站机动方式的目标运动要素估计实验
取 Vs(t)=1450m/s,σβ=0.5°,Δt=2s,V0=15.4kn,C0=65.3°,D0=100.2 链,β0=10.1°,进行数值实验。
首先对观测站等速直航情形,设观测站以速率U = 4kn 沿航向 W = 50°等速直航,则 A(t)= U t eiW,这时传统方法不能给出(V0, C0, D0, β0)的估计。取 Θ的中点作为搜索起点, 上述非线性方法计算的直到T = 600s的最近10个估计见表1。

表1 观测站不机动的估计实验
自表 1可以看出,观测站等速直航情形,非线性方法可以对σβ给出比较精确的估计,对( V0, C0, D0,β0, Vs)的估计则比较差,下面对观测站机动情形进行实验。
假设观测站机动方式为:初始时刻沿观测方位对应的航向航行Tl= 120s,之后向方位增加的反方向转向ΔW = 50°,假设转向运动为匀速圆周运动,角速度为ω = 0.5° /s,转向运动完成后直航Tl时间,之后向方位增加的方向转向ΔW,…,以此类推进行周期为 Tl+ ΔW/ω的机动。其他参数同上,相同项目的一次实验见表2。

表2 观测站机动的估计实验
可以看出,观测站机动给出的目标运动要素估计明显优于观测站不机动的情形。
5 结论
对于观测站不机动目标等速直航的情形,认为Vs= ∞ 将导致对目标方位的观测含有系统误差,单就这个误差看,似乎可以忽略,但所描述的系统的性质根本不同,简单地说,此时若将目标速率与初始距离乘以相同的倍数,则对模型无任何影响,这与实际不符,两种方法的简单比较见表3。
由式(5)(6)可以看出,声速有限决定了可观测的目标方位中包含独立的目标距离信息,认为 Vs= ∞等于放弃了这些信息,除非出于算法简单的目的外,没有理由认为Vs= ∞。

表3 非线性方法与线性方法的简单比较
数值实验发现,线性方法与非线性方法均能给出比较精确的β0的估计,关于V0、C0、D0,线性方法给出的估计稳定很慢且不能稳定于真值附近,非线性方法所给出的估计可以稳定于真值附近。
非线性方法能给出σβ、Vs比较准确的估计,且σβ的估计能很快稳定,也就是说,即使不是出于攻击的目的,在对等速直航目标的纯方位跟踪过程中,可以对这两个参数进行估计。
数值实验发现,Vs(t)= Vs已知的情形,目标运动要素的可观测度明显优于Vs未知的情形。
使用平均声速这一概念可使上面的论述比较简单,然而所得结论的可用性有待于实践检验。
以方位观测误差平方和作为目标函数可以给出性质较优的运动要素的估计,这个目标函数的性质有待于进一步研究。纯方位方法目的是为了跟踪目标当前态势,寻求有利于这一目的的目标函数有待于进一步研究。
以上仿真数值实验中搜索J 的最小值点使用的是Matlab函数lsqnonlin,算法是通用的,虽然较小的σβ有利于提高观测度,但这个算法对置σβ= 0不能立即给出精确的估计,因此就上述非线性方法开发有针对性的快速准确算法是必要的。
[1]Daniel H. Wabgner,W. Charles Mylander, Thomas J.Sanders.海军运筹分析[M](第3版).姜青山,郑保华译.,国防工业出版社,2008.
[2]董志荣.纯方位系统定位与跟踪的本载体最优轨线方程及其最优轨线[J].指挥控制与仿真,2007.29(1):7-15.
[3]潘志坚,阎福旺,刘孟奄,等.纯方位水下目标运动分析方法研究[J].声学学报,1997,22(1):87-92.
[4]石章松,刘忠. 单站纯方位目标跟踪系统可观测性分析[J].火力与指挥控制, 2007,32(2):26-29.
[5]Robert J. Urick.水声原理[M].第 3 版.哈尔冰:哈尔滨船舶工程学院出版社,1990.
[6]Frieden David R.海军武器系统原理[M].第9版.上海翻译出版公司, 1991.

