解析几何中“设而不求”的常用技巧

●赵忠平 (永昌县第一高级中学 甘肃永昌 737200)

解析几何综合问题作为每年数学高考的压轴题型之一，能够有效地考查学生的思维能力和运算能力.由于解题过程中经常出现大量的参数，需要用到“设而不求”的思想方法进行消参，许多学生感到运算难度大、解题正确率低.本文总结解析几何中“设而不求”的几种常用技巧，仅供参考.

1 利用曲(直)线定义

例1 过圆外一点P(2，-1)引圆x2+y2=1的2条切线，求经过2个切点的直线方程.

分析设2个切点分别为 P1(x1，y1)，P2(x2，y2)，则切线方程为

因为切线方程过点P(2，-1)，所以

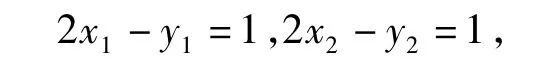
可见 P1(x1，y1)，P2(x2，y2)都满足方程 2x-y=1.因此，经过2个切点的直线方程为2x-y=1.

例2 已知双曲线的方程是16x2-9y2=144，F1，F2是双曲线的左、右焦点，点P在双曲线上，且|PF1|·|PF2|=32，求∠F1PF2的大小.

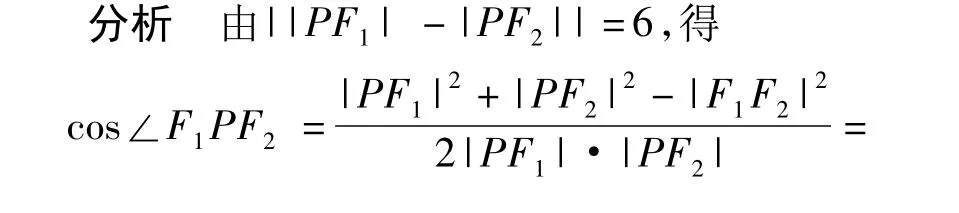
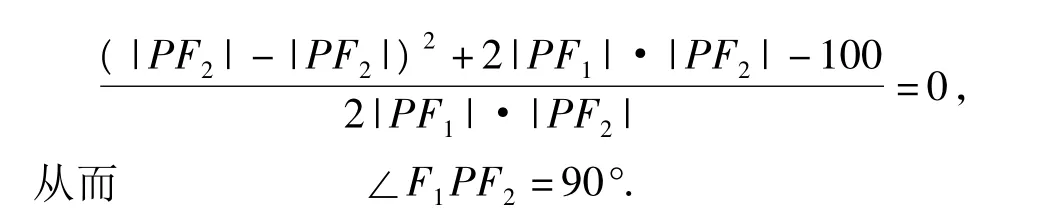
点评曲线定义中往往包含“数”与“形”的特征，巧妙运用曲线定义可以达到在运算中进行“整体代换”的目的.

2 利用韦达定理

例3 已知圆C：x2+y2-2x+4y-4=0，问是否存在斜率为1的直线l，使l被圆C截得的弦为AB，以AB为直径的圆经过原点O.若存在，写出l的方程;若不存在，请说明理由.

分析设存在这样的直线 l：y=x+b，代入x2+y2-2x+4y-4=0，得

设 A(x1，y1)，B(x2，y2)，则

由题意OA⊥OB，得

将式(1)，式(2)代入式(3)得

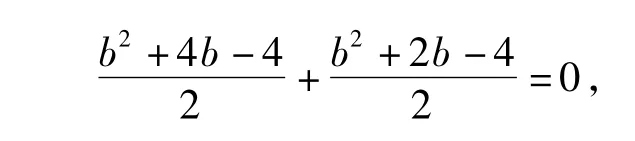
即b=1或b=-4.易验证b=1或b=-4时，Δ＞0，故直线l存在，其方程为y=x+1或y=x-4.

点评直线与曲线位置关系的综合问题一般可以通过联立方程组消去一个变量，得到关于另外一个变量的二次方程，再运用韦达定理表示弦长、面积、弦中点、弦的垂直平分线方程等，在运算中进行“整体代换”，消去多余参数.

3 利用“点差法”

例4 过点M(-2，0)的直线 l与椭圆 x2+2y2=2交于点P1，P2，线段P1P2的中点为P.设直线l的斜率为k1(k1≠0)，设直线OP的斜率为k2，则k1k2= ______.

分析设 P1(x1，y1)，P2(x2，y2)，P(x0，y0)，则

两式相减得

点评与“弦中点”有关的问题或与曲线上2个点斜率有关的问题通常可以运用“点差法”进行“整体代换”，从而简化运算.

4 利用方程“整体”结构

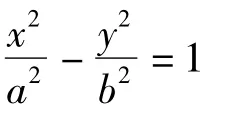
分析设 A1(-a，0)，A2(a，0)，M(x1，y1)，N(x1，-y1)，则直线A1M的方程为

直线A2N的方程为

式(4)×式(5)，得

因为(x1，y1)在双曲线上，所以

当a=b时，轨迹为以原点为圆心、以a为半径的圆;当a≠b时，轨迹为椭圆.

点评利用方程整体结构特点，两式相加或相乘消去多余参数，从整体上实现对方程的化简也是一种常用的“设而不求”技巧.

5 利用焦半径公式

因此AC中点的横坐标为4.

点评与曲线上点到焦点有关的问题常常利用焦半径公式化简，可以起到“整体代换”的作用.

6 利用“特征构造法”

例7 ADB为半圆，AB为半圆直径，O为半圆圆心，且 OD⊥AB，Q为线段 OD的中点.已知|AB|=4，曲线C过点Q，动点P在曲线C上运动且保持|PA|+|PB|的值不变.

(1)建立适当的平面直角坐标系，求曲线C的方程;

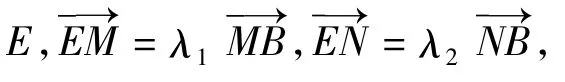
分析(1)略.

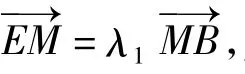
点评由2个结构特征完全相同的等式(或不等式)可以先构造方程(或不等式)，再利用根与系数关系实现“设而不求”.