盘点导数应用的五大“误区”

●陈玉兰 吴志鹏 (德化县第一中学 福建德化 362500)

导数是研究函数性质(单调性、极值、最值等)及其图像的有力工具，但如果对导数的概念、性质理解不到位，就会在解决函数问题时出现不应有的失误，学生在解决导数问题时也就容易出现对而不全的现象.本文结合具体案例，对学生在学习导数过程中出现的易错点进行剖析，希望对读者有帮助和启发.

1 对“过曲线上某点的切线”与“在曲线上某点处的切线”的含义认识模糊

导数的几何意义指出：函数在某点处的导数就是曲线在该点处切线的斜率.由导数的几何意义可知，利用导数求曲线在点x0处的切线方程，可分成以下2步：

(1)求出函数y=f(x)在x0处的导数，即求曲线y=f(x)在点P(x0，f(x0))处切线的斜率;

(2)在已知切点坐标和切线斜率的条件下，求得切线方程为y-y0=f'(x0)(x-x0).

特别地，如果曲线y=f(x)在点P(x0，f(x0))处的切线平行于y轴，这时导数不存在，根据切线定义，可得切线方程为x=x0.

例1 求曲线f(x)=-x3+3x过点A(2，-2)的切线方程.

错解 因为点A在曲线f(x)=-x3+3x上，且 f'(x)=-3x2+3，所以

故所求切线方程为y+2=-9(x-2)，即

正解 设在曲线上的切点为P(x0，y0)因为

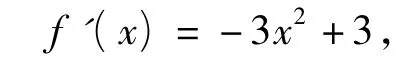
所以在点P处的切线方程为

又因为切线过点A，所以

当x0=-1时，切线经过点 P(-1，-2)和A(2，-2)，切线方程为y=-2;当x0=2时，切线方程为9x+y-16=0.

分析错解中遗漏了y=-2这条切线，失误的原因是把过点A的切线理解成在点A处曲线的切线.曲线在点A处的切线指的是切点在点A处的切线，而过点A的切线除了切点在点A处的切线外，还可能存在切点不在点A处而经过点A的切线，两者是有区别的.因此，解题时必须理清头绪，分清这2个易混淆的概念.其实，“曲线在某点处存在切线”不是“过曲线上某点存在切线”的充分必要条件，而是充分不必要条件.

2 误认为切线斜率的取值范围与割线斜率的取值

范围等价

例2 已知函数f(x)=-x3+ax2(a∈R)，若函数图像y=f(x)上任意2个不同点的连线斜率小于1，求实数a的取值范围.

错解因为f(x)=-x3+ax2(a∈R)，所以

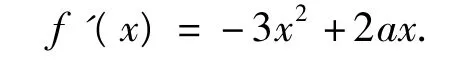
又因为函数y=f(x)图像上任意2个不同点的连线斜率小于1，所以f'(x)＜1，即

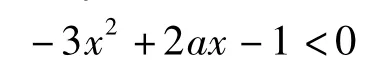
对任意x∈R恒成立，从而

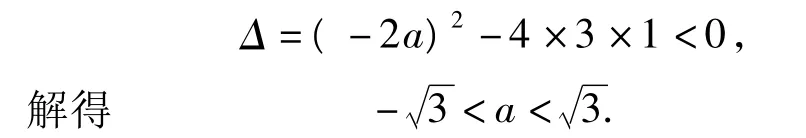
分析由拉格朗日中值定理，若函数f(x)满足：

(1)在［a，b］连续;

(2)在(a，b)可导，

由这个定理可知，连续函数的图像在［a，b］上任意2个点的连线总与它在(a，b)上的某条切线平行，即f(x)在［a，b］上任意2个点的割线斜率与其在(a，b)上某点ζ处的切线斜率相等.由拉格朗日中值定理获得的结论并不具有充要性，错解中f'(x)＜1是f(x)任意2个点连线斜率都小于1的充分不必要条件，即f(x)在R上任意2个点连线斜率的取值范围是其导函数f'(x)值域的子集.也就是说，对于某一点处的导数，不存在函数f(x)上2个点连线斜率与之相等.

例如，函数f(x)=x3，设其图像上的任意2个点为(x1，y1)，(x2，y2)(x1≠x2)，则过这 2 个点连线的斜率为

而f'(x)=3x2≥0，显然切线斜率的取值范围与割线斜率的取值范围并不等价.

正解1 (构造函数法)

不妨设 x1，x2∈R，且 x1＜x2，则

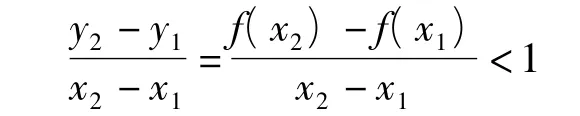
恒成立，即f(x2)-x2＜f(x1)-x1成立.令g(x)=f(x)-x=-x3+ax2-x，则

即函数g(x)为R上的减函数，故

对x∈R恒成立，即

正解2 (放缩法)

设曲线上任意 2 个点为(x1，y1)，(x2，y2)(x1＜x2).由题意得

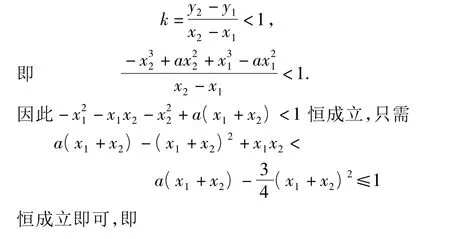
3 错解了“导数为0”与“有极值”的逻辑关系

对于满足 f'(x0)=0的点 x0(称为驻点)，f'(x0)=0是x0为函数f(x)的极值点的必要而非充分条件.如果把驻点等同于极值点，则容易导致错误.

错解由已知得

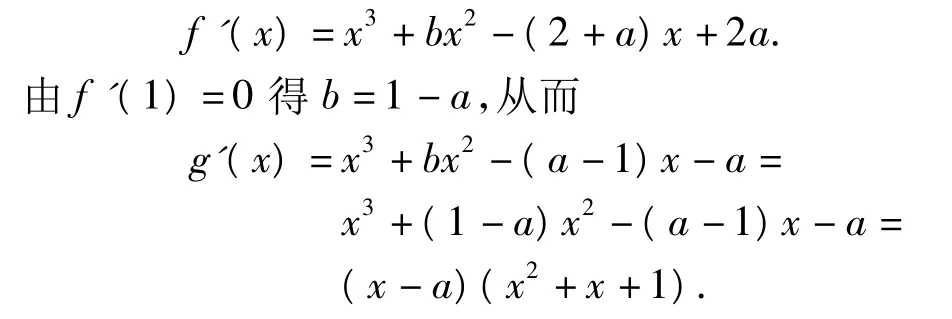
因此当 x＜a时，g'(x)＜0，即 g(x)在(-∞，a)上单调递减.由(a-6，2a-3)⊆(-∞，a)，得

故所求的取值范围为-3＜a≤3.

分析以上解法忽略了一个小细节，解题过程中用到f'(x)=0，即x=1是f(x)的驻点，那x=1是不是函数的极值点呢?

如果a=1，那么x=1就只是函数f(x)的拐点而非极值点，而由条件知f(x)在x=1处取得极值，因此应排除a=1.从而实数的取值范围应是-3＜a＜1且1＜a≤3.

一个可导函数在某点处的导数为0是在该点取极值的必要而非充分条件，即可导函数在某处取得极值，则函数在此处的导数值必等于0;反之，若导数在某处的值为0，则函数在该处不一定取得极值，还须进一步检验f'(0)在f'(x)=0的根的左右2边的导数值的符号.

4 误认为极值只能在导数为0的点处取得

设函数f(x)在点x0附近有定义，且若对x0附近的所有的点都有 f(x)＜f(x0)(或 f(x)＞f(x0))，则称f(x0)为函数的一个极大(小)值，称x0为极大(小)值点.

求可导函数f(x)极值的步骤：

(1)求导数f'(x)，令f'(x)=0.

(2)求方程f'(x)=0的根.

(3)检验f'(x)在方程f'(x)=0的根的左右侧的符号.如果在根的左侧附近为正，右侧附近为负，那么函数y=f(x)在这个根处取得极大值;如果在根的右侧附近为正，左侧附近为负，那么函数y=f(x)在这个根处取得极小值.

例4 求函数f(x)=|x2-2x-3|的极值.错解 因为

令 f'(x)=0，得x=1.当 -1＜x＜1时，f'(x)＞0;当1＜x＜3时，f'(x)＜0.因此当x=1时，函数有极大值4.

分析在确定极值时，只讨论满足f'(x)=0的点x0附近导数的符号变化情况是不全面的，在导数不存在的点处也可能存在极值.在上述解法中，显然忽视了讨论x=-1和x=3处导数不存在的情况，从而产生了丢根的情况.正确的结果还应包括在x=-1和x=3处函数取到极小值0.当然，本题若直接画出函数图像，则一目了然了.

5 曲解了“导数值的符号”与“函数单调性”的关系

设函数f(x)在某个区间内可导，若在此区间f'(x)＞0，则 f(x)在此区间内为增函数;若f'(x)＜0，则f(x)在此区间内为减函数.利用导数解决函数的单调性问题时，除了掌握以上依据外，还应明确以下几点(现以增函数为例来说明)：

(1)f'(x)＞0是可导函数f(x)在定义域内单调递增的充分不必要条件.如函数f(x)=x3在(-∞，+∞)上单调递增，但f'(x)≥0.

(2)f'(x)≥0是可导函数f(x)在定义域内单调递增的必要不充分条件.若f(x)为增函数，则一定有f'(x)≥0，但反之不一定成立：因为f'(x)≥0为f'(x)＞0或f'(x)=0两者之一成立即可.当函数在某个区间内恒有f'(x)=0，则f(x)为常数，函数不具有单调性.

(3)f'(x)≥0且f'(x)在定义域内的任意子区间不恒为0是可导函数f(x)在定义域内单调递增的充要条件.

例5 已知函数f(x)=ax3-x2+x在R上是增函数，求实数a的取值范围.

错解函数f(x)的导数

因此f'(x)＞0在R上恒成立，故

解不等式f'(x)＜0，可得可导函数的单调递减区间;反之，若函数f(x)在区间D上为减函数，则f'(x)≤0在区间D上恒成立，在解题时往往易漏掉等号.

总之，导数是解决有关问题的重要工具，若在应用时能注意到以上的细节，则能准确解题.