对一道武汉市调研考试题的研究

☉湖北省阳新县白沙中学 董才强

对一道武汉市调研考试题的研究

☉湖北省阳新县白沙中学 董才强

著名的数学教育家G.波利亚说过：“没有任何一道题是可以解决得十全十美的，总剩下些工作要做，经过充分的探讨总结，总会有点滴的发现，总能改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平.”事实上，许多貌似平凡的问题其实意境幽深，均可成为曲径通幽处.只要我们做一个敏锐的探索者，就会发现散落于其中的晶莹的数学珍珠.如2011年5月份湖北省武汉市九年级数学调研考试题：

如图1，⊙O是△ABC的外接圆，AE是⊙O的直径，AD是△ABC中BC边上的高，EF⊥BC，垂足为F.

（1）求证：BF=CD；

（2）若CD=1，AD=3，BD=6，求⊙O的直径.

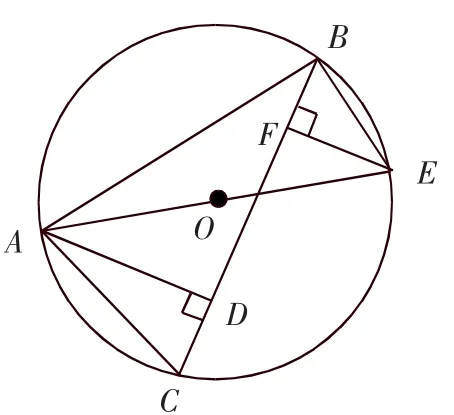
图1

一、整合思路，探求解法

本题融几何证明、计算于一体，题型较为常见，但是对学生而言有一定的难度，主要难在第（1）问，不少学生甚至无从下手.究其原因，可能是初中学生对线段相等的证明习惯于依赖三角形的全等，思路和方法狭窄单一.其实证明两条线段相等的方法有好多种，常用的方法是运用“等角对等边”或三角形的全等，当这两个思路行不通时，不妨寻找相似三角形，再借助比例线段的转化，这样也能够证明两条线段相等；在圆中还可以通过弦、弧、角（圆心角或圆周角）的相互转化来证明线段相等.如果学生对这些思想方法能够熟练灵活运用，解答此题就轻松自如了.

（1）证法1：构造全等三角形.

如图2，延长EF交⊙O于点G，连接BG.

由AE是⊙O的直径，得∠ABC+∠CBE=90°.

由EF⊥BC，得∠BEG+∠CBE=90

图2

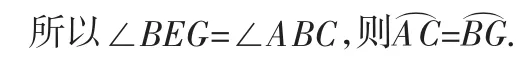
所以AC=BG. ①

所以∠C=∠GBF. ②

由AD是△ABC中BC边上的高，EF⊥BC，得∠ADC=∠GFB=90°. ③

根据①、②、③，可得△ADC≌△GFB.

所以BF=CD.

评注：不少学生误认为△ADC≌△EFB，在这种错觉思维的影响下，为寻找这两个三角形全等的条件而绞尽脑汁，最终无功而返，证明失败.

证法2：应用平行线分线段成比例定理.

如图3，作OH⊥BC，垂足为H，则BH=CH.

由AD⊥BC，EF⊥BC，得EF∥OH∥AD.

又OA=OE，则HD=HF.

所以BH－HF=CH－HD，即BF=CD.

评注：“过圆心作弦的垂线段”是圆中一条重要的辅助线，解题时学生可能会想到这一点，但是由于对平行线分线段成比例定理的变式图形不熟悉（像图3这样的平行线分线段成比例的变式图形，课本上没有，有些教师也未向学生提及），即使作出了图3中的辅助线，学生还是不知道如何下手.

证法3：应用相似三角形.

如图1，由AE是⊙O的直径，AD是△ABC中BC边上的高，

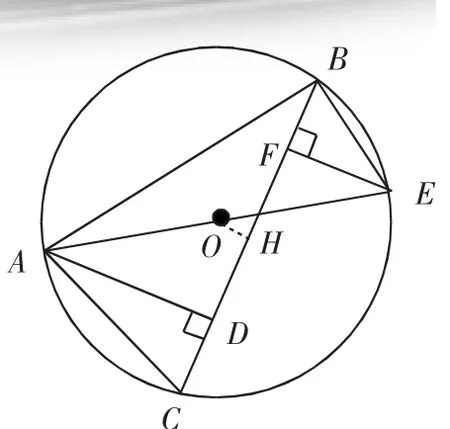
图3

评注：有些学生在没有找到全等三角形后，马上转向寻找相似三角形，少数学生证出了结论.遗憾的是，部分学生被众多的比例线段套牢，不能寻找有效的线段比去进行沟通和转化，导致思路和方法正确而证明失败.

（2）如图1，根据题意可知△ACD和△ABD都是直角三角形.

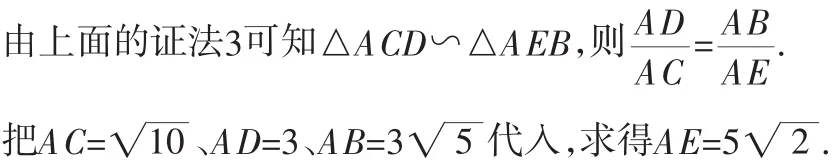
评注：第（2）问比第（1）问简单许多，部分学生懂得“跳步作答”，即越过第（1）问直接解答第（2）问，做到了“能得分处莫丢分”.

二、深入挖掘，提炼结论

这道试题的第（2）问虽然“其貌不扬”，但内涵丰富，其间蕴含有三角形的一个美妙性质.如果觉得此问平淡无奇而“来也匆匆，去也匆匆”，一个重要的结论恐怕就“藏在深闺无人识”了.

概括这道调考题第（2）问的结构特征，我们不难提炼出定理1.

定理1 三角形的任意两边之积等于第三边上的高乘以外接圆直径.

为不失一般性，这里再以钝角三角形为例予以证明.

如图4，⊙O是△ABC的外接圆，AE是⊙O的直径，AD是△ABC中BC边上的高，求证：AB·AC=AD·AE.

证明：连接BE.由AE是⊙O的直径，AD是△ABC中BC边上的高，得∠ABE=∠ADC=90°.

由A、C、B、E四点都在⊙O上，得∠ACD=∠AEB.

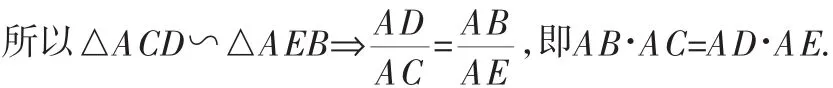
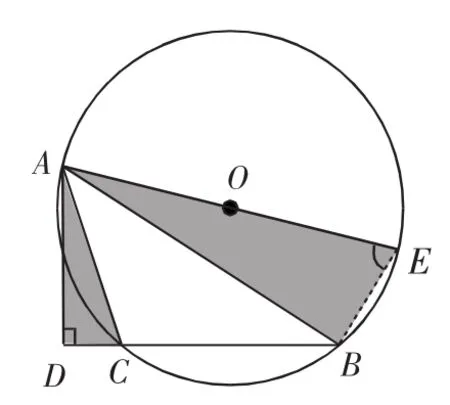
图4

三、联想化归，灵活应用

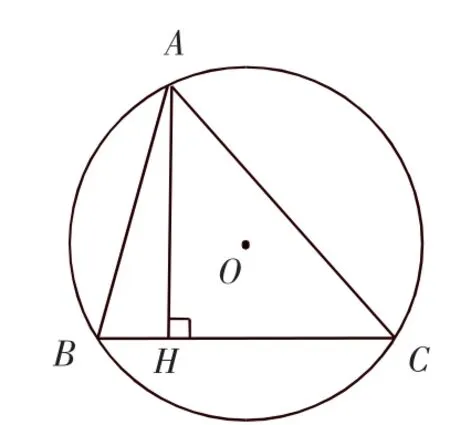
图5

例1（2010年黄石中考）如图5，△ABC内接于⊙O，AH⊥BC于H，若AB+AC=12，AH=3，则⊙O的半径R的最大值为______.

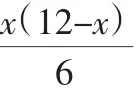
例2 如图6，P为⊙O上一点，⊙O的弦AB切⊙P于C，若⊙O和⊙P的半径分别为5和2，求PA·PB的值.

简解：连接PC，则PC⊥AB，即PC是△PAB中AB边上的高.根据定理1可得PA·PB=2R·PC，其中2R就是△PAB的外接圆（即⊙O）的直径.由题意可知R=5，PC=2，所以PA·PB=10×2=20.

例3 在△ABC中，AB=AC=10，BC=12，求△ABC的外接圆的半径.

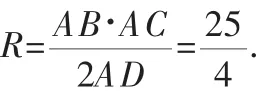
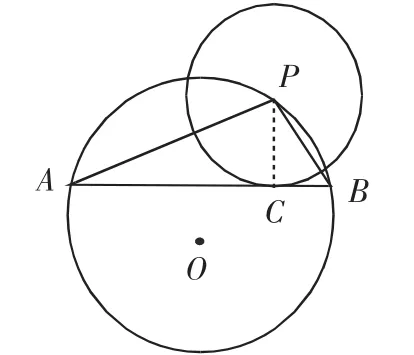
图6

四、由此及彼，更上层楼

在解答完例3后，心理似乎还不满足：如果给出的是一个任意三角形的三条边长，怎样求其外接圆的半径呢？通过对定理1的再思考，得到定理2.

一道普通平凡的试题，孕育着不平凡的方法和结论，给人带来更为深入广泛的思考.通过这个探究过程，大大拓宽了我们的知识视野（得到任意三角形的外接圆半径公式），这是在源源不断的思考和探索中得到的珍宝.

一滴水可以折射出太阳的光辉，一道题能够散发出智慧的光芒，解题并不在于多多益善，不断总结、反思我们的解题思路和方法，提炼、升华问题中的本质属性，对扩大教师的数学视野、提高教师的专业素养大有裨益.