绝对值方程的一种严格可行内点算法

雍龙泉, 刘三阳, 张建科, 陈 涛, 邓方安

(1. 西安电子科技大学 应用数学系, 西安 710071; 2. 陕西理工学院 数学与计算机科学学院, 陕西 汉中 723001;3. 西安邮电学院 理学院, 西安 710121)

1 绝对值方程

考虑如下问题：

u=Au-b,

(1)

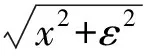
本文在假设矩阵A的奇异值大于1(这里矩阵A的奇异值定义为矩阵ATA特征值的非负平方根)时, 提出一种绝对值方程的新算法----可行内点算法, 并证明了该算法经过多次迭代后收敛到原问题的最优解, 数值实验表明该方法是有效的.

2 算 法

定义1如果对∀x∈Rn,x≠0, 都有xTMx≥0, 则矩阵M∈Rn×n称为半正定矩阵. 如果对∀x∈Rn,x≠0, 都有xTMx>0, 则M称为正定矩阵. 这里定义的(半)正定矩阵不要求对称性, 因此, 这样定义的(半)正定矩阵也称为广义(半)正定矩阵[14]. 显然, 广义(半)正定矩阵包含对称(半)正定矩阵. 若无特殊说明, 本文所涉及的正定矩阵均为广义(半)正定矩阵.

线性互补问题: 即求一个向量x∈Rn, 满足x≥0,Mx+q≥0,xT(Mx+q)=0, 线性互补问题简记为LCP(M,q). 当矩阵M是半正定矩阵时, 称LCP(M,q)为单调线性互补问题.

引理1[15]若矩阵A的特征值不为1, 则AVE可以转化为LCP(M,q), 其中:

M=(A+I)(A-I)-1;q=((A+I)(A-I)-1-I)b;x=(A-I)u-b.

引理2[15]若矩阵A的奇异值大于1, 则矩阵M=(A+I)(A-I)-1是一个正定矩阵.

定理1[15]若矩阵A的奇异值大于1, 则对任意的b∈Rn, AVE存在唯一解.

下面通过求解线性互补问题获得问题(1)的解. 求解线性互补问题的算法有很多, 如投影法、 内点法、 非光滑牛顿法和光滑牛顿法等[16-19]. 本文借鉴文献[19]中求解线性互补问题的思想, 将牛顿方向和中心路径方向相结合, 通过求解一个线性方程组得到搜索方向; 在每次迭代中, 寻找新的迭代点, 使得新的迭代点仍满足可行性, 同时使得优化目标值减少, 这样通过有限次迭代即可获得原问题的一个近似解.

为了求解LCP(M,q), 构造如下优化问题：

(NP) minxTy; s.t.y=Mx+q,x≥0,y≥0.

显然, 当且仅当问题(NP)达到最优目标值0时, 对应的(x,y)是LCP(M,q)的一个解.

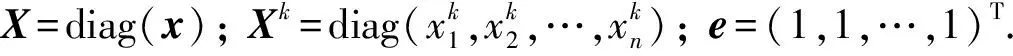
下面将建立一种算法, 使得该算法产生的点列在中心路径邻域内, 即{(xk,yk)}⊂N(a), 且使得(xk+1)Tyk+1≤ρ(xk)Tyk(k=0,1,…), 其中ρ∈(0,1)是一个与k无关的常数. 这样, 通过有限步迭代即有(xN)TyN≤ε, 且(xN,yN)∈N(a).

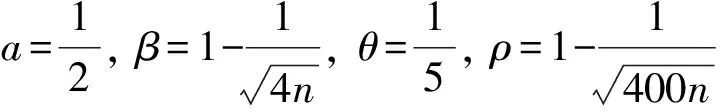
算法1

取命题1中的参数a,β,ρ,θ,ε>0为容许误差, (x0,y0)∈N(a)为给定的初始点,k∶=0;

1) 若(xk)Tyk≤ε, 则停, 得到近似最优解(xk,yk), 否则转2);

2) 寻找转移方向(Δx(β),Δy(β)), 其中(Δx(β),Δy(β))由下列方程组确定：

3) 令xk+1∶=xk+θΔx(β),yk+1∶=yk+θΔy(β),k∶=k+1, 转1).

3 收敛性分析

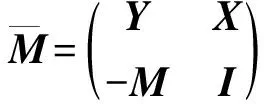
证明参见文献[20].

由引理3知, 在算法1步骤2)中, 转移方向(Δx(β),Δy(β))存在且唯一.

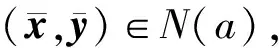
记方程组(2)的解为(Δxa,Δya), 方程组(3)的解为(Δxc,Δyc). 显然在算法1中, 转移方向

Δx(β)=βΔxc+(1-β)Δxa, Δy(β)=βΔyc+(1-β)Δya;

因此, 在算法1中, 转移方向(Δx(β),Δy(β))是牛顿方向(Δxa,Δya)和中心路径方向(Δxc,Δyc)的严格凸组合.

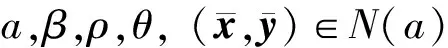
2)

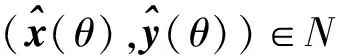
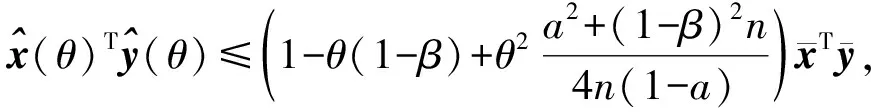
根据引理4, 有:

定理2取命题1中的参数a,β,ρ,θ, (x0,y0)∈N(a)为初始点, 则算法1产生的点列满足： 1) (xk,yk)>0; 2) (xk,yk)∈N(a); 3) (xk+1)Tyk+1≤ρ(xk)Tyk. 其中k=0,1,2,…

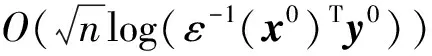
证明: 由定理2可知(xk+1)Tyk+1≤ρ(xk)Tyk(k=0,1,2,…), 因此有

4 数值实验

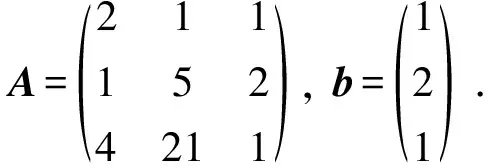
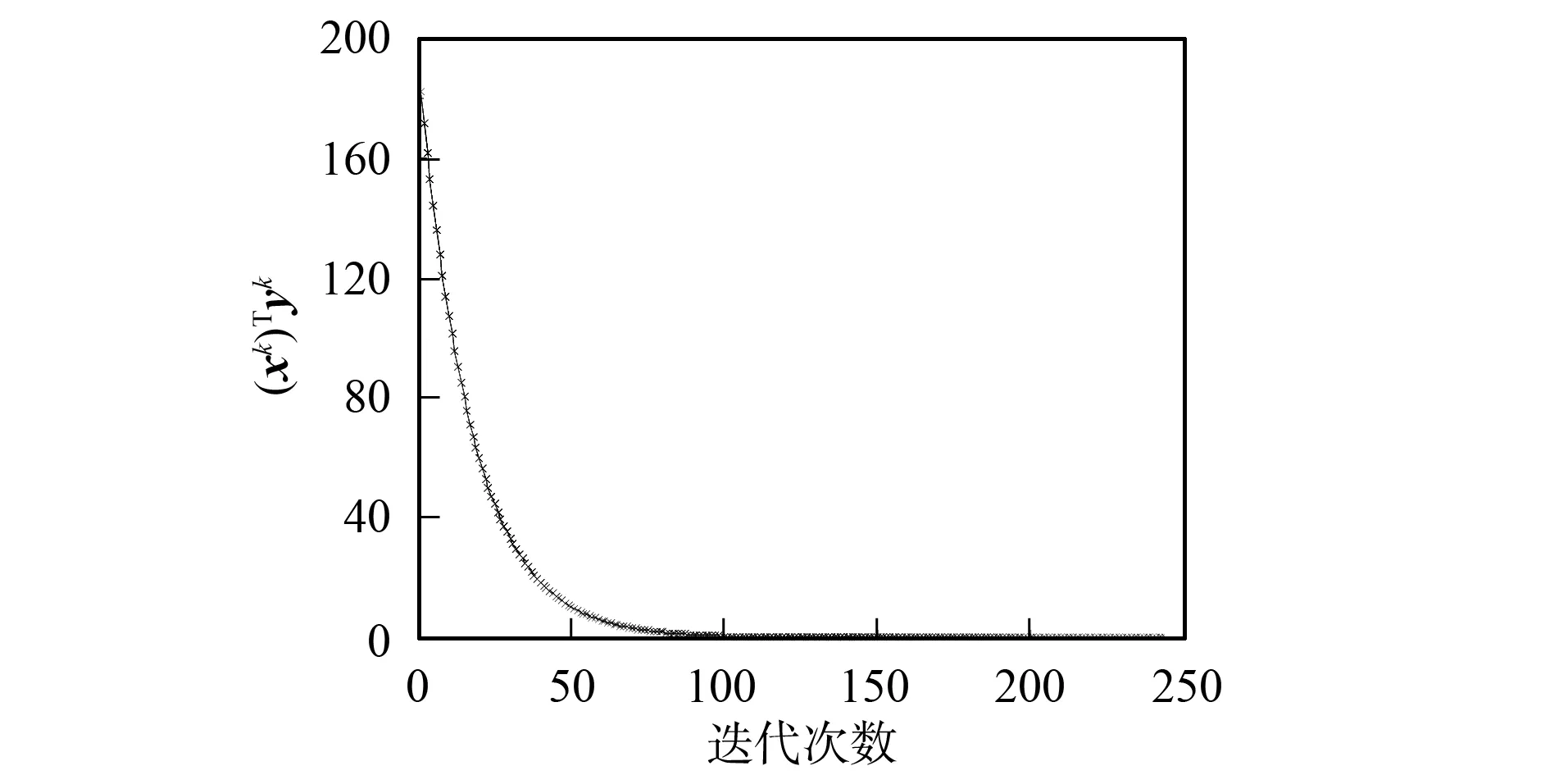
图1 目标函数值xTy的下降过程Fig.1 Descent of xTy

由于矩阵A的奇异值为(22.070 5,2.271 2,1.316 7)>1, 因此矩阵M为正定矩阵, 相应的LCP(M,q)具有唯一解. 用本文算法进行求解, 经过247次迭代后, 得到线性互补问题的解为x=(0.000 2,0.000 5,0)T, 优化问题(NP)的目标函数值xTy下降过程如图1所示. 从而AVE问题的唯一解为

进一步, 用算法1求解随机产生的AVE问题, 这里矩阵A和向量b由下述Matlab代码产生:

rand(“state”,0);

R=rand(n,n);

b=rand(n,1);

A=R′*R+n*eye(n);

M=(A+eye(n))*(inv(A-eye(n)));

q=((A+eye(n))*(inv(A-eye(n)))-eye(n))*b;

输入矩阵A的阶数n, 给定初始点后, 可以快速得到AVE问题的解. 表1列出了不同维数的计算结果, 其中k表示(计算机)执行算法1获得近似解所需的迭代次数.

表1 不同维数的计算结果

数值实验表明, 本文算法对求解此类绝对值方程十分有效, 鉴于该算法具有多项式复杂性, 因此该算法可以作为求解此类问题的一种有效方法.

[1] Mangasarian O L, Meyer R R. Absolute Value Equations [J]. Linear Algebra and Its Applications, 2006, 419(2): 359-367.

[2] Mangasarian O L. Absolute Value Programming [J]. Computational Optimization and Aplications, 2006, 36(1): 43-53.

[3] Mangasarian O L. Absolute Value Equation Solution via Concave Minimization [J]. Optim Lett, 2007, 1(1): 3-8.

[4] Mangasarian O L. A Generlaized Newton Method for Absolute Value Equations [J]. Optim Lett, 2009, 3(1): 101-108.

[5] Mangasarian O L. Knapsack Feasibility as an Absolute Value Equation Solvable by Successive Linear Programming [J]. Optim Lett, 2009, 3(2): 161-170.

[6] HU Sheng-long, HUANG Zheng-hai. A Note on Absolute Value Equations [J]. Optim Lett, 2010, 4(3): 417-424.

[7] Prokopyev O. On Equivalent Reformulations for Absolute Value Equations [J]. Computational Optimization and Applications, 2009, 44(3): 363-372.

[8] Zhang C, Wei Q J. Global and Finite Convergence of a Generalized Newton Method for Absolute Value Equations [J]. Journal of Optimization Theory and Applications. 2009, 143(2): 391-403.

[9] Rohn J. An Algorithm for Solving the Absolute Value Equation [J]. Electronic Journal of Linear Algebra, 2009, 18: 589-599.

[10] Caccetta L, QU Biao, ZHOU Guang-lu. A Globally and Quadratically Convergent Method for Absolute Value Equations [J]. Computational Optimization and Applications, 2011, 48(1): 45-58.

[11] WANG Ai-xiang, WANG Hai-jun, DENG Yong-kun. Interval Algorithm for Absolute Value Equations [J]. Central European Journal of Mathematics, 2011, 9(5): 1171-1184.

[12] Muhammad Aslam Noor, Javed Iqbal, Sanjay Khattri, et al. A New Iterative Method for Solving Absolute Value Equations [J]. International Journal of the Physical Sciences, 2011, 6(7): 1793-1797.

[13] Noor M A, Iqbal J, Al-Said E, et al. Residual Iterative Method for Solving Absolute Value Equations [J/OL]. Abstract and Applied Analysis, 2012, doi: 10.1155/2012/406232.

[14] TONG Wen-ting. Generalized Positive Definite Matrix [J]. Acta Mathematica Sinica: English Series, 1984, 27(6): 801-810. (佟文廷. 广义正定矩阵 [J]. 数学学报, 1984, 27(6): 801-810.)

[15] YONG Long-quan. A New Solution Method for Absolute Value Equations [J]. Science and Technology Review, 2010, 28(5): 60-62. (雍龙泉. 绝对值等式问题的一个求解方法 [J]. 科技导报, 2010, 28(5): 60-62.)

[16] KOU Shu-shun. Existence of Solutions for Linear Complementarity Problem [J]. Applied Mathematics and Mechanics, 1995, 16(7): 641-643. (寇述舜. 关于线性互补问题解的存在性 [J]. 应用数学和力学, 1995, 16(7): 641-643.)

[17] Kojima M, Megiddo N, Yoshise A. A Unified Approach to Interior Point Algorithms for Linear Complementary Problem [M]. Lecture Notes in Computer Science, Vol.538. Berlin: Springer-Verlag, 1991.

[18] 韩继业, 修乃华, 戚厚铎. 非线性互补理论与算法 [M]. 上海: 上海科学技术出版社, 2006.

[19] YONG Long-quan, DENG Fang-an, CHEN Tao. An Interior Point Method for Solving Monotone Linear Complementarity Problems [J]. Journal of Math, 2009, 29(5): 681-686. (雍龙泉, 邓方安, 陈涛. 单调线性互补的一种内点算法 [J]. 数学杂志, 2009, 29(5): 681-686.)

[20] YONG Long-quan, LIU San-yang. The Proof and Application of a Series of Nonsingular Matrixes in Interior Point Algorithm [J]. Mathematics in Practice and Theory, 2006, 36(2): 258-261. (雍龙泉, 刘三阳. 内点算法中一类非奇异矩阵的证明及其应用 [J]. 数学的实践与认识, 2006, 36(2): 258-261.)

[21] YONG Long-quan. The Study of Algorithms for Quadratic Programming [D]: [Master’s Degree Thesis]. Xi’an: Xidian University, 2005. (雍龙泉. 二次规划的算法研究 [D]: [硕士学位论文]. 西安: 西安电子科技大学, 2005.)