一些简单有限连通图的连通包数

马儇龙，金剑行，钟 国

(广西师范学院 数学科学学院，广西 南宁530023)

本文中所考虑的图均是简单有限的连通图，即没有环和重边的无向有限连通图。对于一个有限集合S，通常用|S|表示S中元素的个数。设G=(V，E)是一个图，这里V和E分别表示这个图G的顶点集和边集，|V|和|E|分别称为G的阶(order)和大小(size)。如果G中任意两个顶点都相连，则这个图称为是完全的。特别地，阶为n的完全图记作Kn。degG(v)表示G中顶点v的度(degree)，当上下文不引起混淆时，可简单记为deg(v)。设S⊆V，则G［S］表示由点集S诱导的G的子图。用NG(v)表示G中顶点v的邻域(neighborhood)，是指与v相邻接的所有点组成的集合，也可以简单记作NG(v)。如果由点v的邻域NG(v)所诱导的G的子图是完全的，则称v是G的一个极点(extreme－vertex)。对于连通图G=(V，E)的顶点c，如果由V{c}诱导G的子图是不连通的，则称c是G的一个割点(cut－vertex)。如果图G是一条长(或阶)为n的路，则G可记之为Pn;如果图G是一个阶为n的圈，则可记其为Cn。

图G中，若顶点u和v之间至少有一条路连接，则G中最短u－v路的长称为u和v之间的距离(distance)，且记为d(u，v)。一个连通图G的直径(diameter)是图中任两点距离的最大值且被记作diam(G)。一条长为d(u，v)的u－v路称为一条u－v测地线(geodesic)。对于一个顶点x，如果x位于某一条u － v测地线P上，则x被称为位于u － v测地线上。对于两个顶点u和v，I［u，v］是所有位于u － v测地线上的点的集合。对于V的一个子集S，则I［S］表示位于集合S中任意两个顶点u和v的u －v测地线上的点的集合之并，即如果对于任意的集合S(⊆V)有I［S］= S，则S称为是一个凸集(convex set)。若S={v}或S=V，则明显S是凸的。图G的凸数(convexity number)是使得S(⊆V)是一个凸集的S的最大的势(cardinality，或|S|)，即集合S里面元素的个数，并且G的凸数被记作C(G)。集合S的凸包是指最小的包含S的凸集并且它被记作Ih(S)(由于两个凸集的交仍是凸集，故一个集合的凸包是唯一的，进而凸包的定义是合理的)。如果I［S］=V和Ih(S)=V，则S分别称为G的测地集(geodetic set)和包集(hull set)，测地集在文献［1 －3］中作者已经做了充分的研究，而包集在文献［2 －4］中作者也做了许多研究。G的测地数g(G)是G的所有测地集势的最小值。类似地，G的包数h(G)是G的所有包集势的最小值。

一个连通图的连通包数首次提出是在文献［5］中，作者研究了一些连通包数的基本性质且提出了一些有待解决的问题。本文是关于连通包集的进一步的研究。对于有关图论的一些常见术语和定义，请参考文献［6］。

1 连通包数的定义

定义1.1 设G=(V，E)是一个图且集合S⊆V。如果S是一个包集且使得G的子图G［S］是连通的，则S称为G的一个连通包集。所有连通包集中最小的势叫做G的连通包数且被记作hc(G)。

例1.2 对于图1，设S1={v1，v6}，则d(v1，v6)=3，因此I［S1］={v1，v2，v3，v5，v6}。注意到I［S1］不是凸集(因为v4∉I［S1］，但v4∈I［I［S1］］)。于是这个图的顶点集V={v1，v2，v3，v5，v6}是包含S1的最小的凸集，即Ih(S1)=V并且S1是图G的一个包集，进而h(G)=2。注意到G［S1］是不连通的，因此S1不是G的连通包集.现在考虑S2={v1，v2，v3，v6}，显然I［S1］={v1，v2，v3，v5，v6}，易知Ih(S2)=V，故S2是G的一个包集.这时注意到G［S2］是连通的，于是S2是G的一个连通包集。更进一步，可以证明hc(G)=4。另一方面容易看出S3={v1，v2，v3，v6}也是G的一个连通包集。

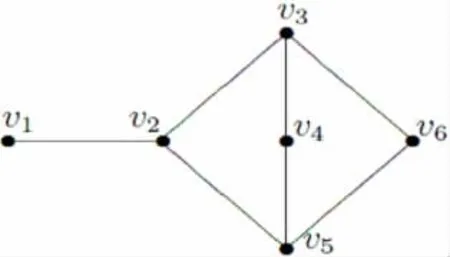
图1 G=(V，E)

2 一些连通图的连通包数

引理2.1 设G=(V，E)是一个连通图且S是V的任意一个子集，则有S⊆I［S］⊆Ih(S)⊆V。

证明 注意到Ih(S)是一个凸集且包含S，于是I［Ih(S)］=Ih(S)，当然I［S］⊆I［Ih(S)］=Ih(S)，即I［S］⊆Ih(S)，引理的其它部分显然成立。

定理2.2 设n≥2 且G=(V，E)≌Pn，则hc(G)=n。特别地，V是G的一个最小连通包集。

证明 设Pn为路v1v2…vn－1vn，考虑到Pn的连通包集所诱导的子图是连通的，于是Pn的任何一个连通包集均是这条路上的一个截断。因此不妨假设S={vi，vi+1，…，vj－1，vj}是Pn的一个连通包集.这里下标i，i+1，…，j－1，j对应于自然数集的一个截断，这说明由G［S］是连通的。注意到I［S］=S，进而S是凸的，根据包集的定义可知S=V。这说明Pn的任何一个连通包集均是Pn的顶点集。故Pn的任何一个最小连通包集也是Pn的顶点集，即hc(G)=n，定理得证。

证明 设Cn为圈v1v2…vn－1vnv1，考虑到Cn的连通包集所诱导的子图是连通的，故Cn的任何一个连通包集均是这个圈上的一些连续邻接的顶点组成。因此不妨假设S={vi，vi+1，…，vj－1，vj}是Cn的一个连通包集，这里下标i，i+1，…，j－1，j对应于集合{1，2，…，n－1，n，1，2，…}的一个截断，这说明由I［S］是连通的。考虑两种情况:

定理2.4 设G(V，E)是一个阶为n的树，则hc(G)= n。

证明 反证。假设hc(G)≠n，则hc(G)＜n且G存在一个最小连通包集S使得| S| ＜| V|。因此I［S］≠S(否则，S是个凸集，这意味着包含S的最小凸集就是它本身，根据包集定义可知S = V，这是一个矛盾。)，即存在x∈V使得x∈I［S］但x∉S。故x必位于一条u －v测地线上，这里u，v∈S。于是d(u，v)≥2，这时注意到u，v在G［S］中是连通的，不妨设uw1w2…wiv是G［S］中的使得u，v连通的一条路。既然x∉S但x位于一条u － v测地线上，故又可以设uo1o2…x…oiv是G［I［S］］中的使得u，v连通的一条路，这说明uw1w2…wivoi…x…o2o1u是图G的子图G［I［S］］中的一个圈，即它也是图G的一个圈，注意到G是树，故G中是不含有圈的，这是一个矛盾。因此假设不成立，即hc(G)= n。

定理2.5 设G(V，E)是一个完全二部图Kr，s，则

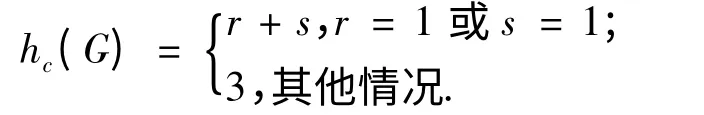
证明 对于完全完全二部图Kr，s，如果r=1 或者s=1，则Kr，s是一个星图，也就是说Kr，s为一棵树。于是根据定理3.4 可知，hc(G)=r+s。现在设r≠1 且s≠1，考虑下面的两种可能情况。

情况1:r=2 或者s=2。不妨假设r=2。若s=2，则G≌C4且hc(G)=3。否则，图G如图2 所示，可以断言S={u，v，w}是G的一个连通包集，这是因为I［S］=V，即I［S］⊆Ih(S)=V.显然G［S］是连通的，故S={u，v，w}是势最小的连通包集，也就是说此时hc(G)=3。

情况2:r≠2 或者s≠2。这种情况下图G如图3 所示(图中顶点集{y1，y2，…，yi}中的每个顶点均和顶点集{x1，x2，…，xi}中每个顶点邻接)，容易看出{u，y1，y2，…，yi，v}和{x1，x2，…，xi，w}是G的两个划分集。在这种情况下我们断言hc(G)=3。令S={u，v，w}，则I［S］={u，v，w，x1，x2，…，xi}。由于集合{y1，y2，…，yi}中的每一个点都位于x1－w测地线上而{y1，y2，…，yi}中的每一个点都不含在I［S］中，故I［S］不是凸集。进一步，由于I［S］⊆Ih(S)=V，注意到Ih(S)是凸集，故Ih(S)包含x1－w测地线上的每一个点，于是不得不有Ih(S)=V。这意味着S={u，v，w}是G的一个连通包集，另一方面，显然S又是G的一个势最小的连通包集，因此断言成立。

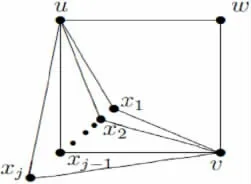
图2 hc(G)=3

图3 hc(G)=3

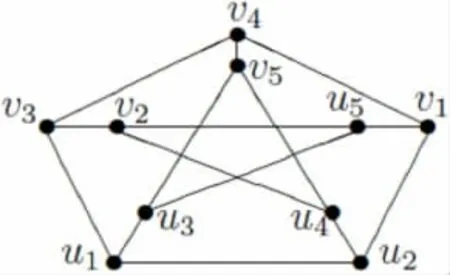
图4 Petersen 图

定理2.6 设G(V，E)是Petersen 图，则hc(G)=5。

证明 设G(V，E)是Petersen 图，则G是一个阶为10 的3 －正则立方图，显然diam(G)=2，见图4。明显对Petersen 图有hc(G)≥4。下面就hc(G)的大小问题考虑两种情况。

情况1:若hc(G)=4，则图G存在一个最小的连通包集S使得|S| =4 且G［S］是G的连通子图。4个顶点的连通简单图有6 个(见图5)。从直观上看出，Petersen 图G是不存在C3或C4作为其子图的，因此G［S］只能同构于P4或者星图K1.3(分别为图5 里面的前两个)。现考虑两种可能:(1)G［S］≌P4。这时易知G［I［S］］≌C5，而明显G［I［S］］的顶点集在V中是凸的，于是I［S］是凸集，即I［S］成了G中包含S的最小凸集，根据连通包集的定义可知I［S］=V，这是一个矛盾。(2)G［S］≌K1.3，这时注意到diam(G)=2 且图G中任二顶点的距离为2 的路是唯一的，于是I［S］=S，即表明S是凸集，根据连通包集定义同理可知I［S］=S=V，又一个矛盾。综合这两种可能可知hc(G)≠4。

图5 阶为4 的简单连通图(同构意义下只有6 个)

情况2:考虑hc(G)≥5。令S={u1，u2，u3，u4，u5}(对应于图4 中的顶点标号)。则I［S］={u1，u2，u3，u4，u5，v1，v2，v5}，由于v4位于v1－v5测地线上而v4∉I［S］，因此I［I［S］］≠I［S］，即I［S］不是凸集。根据引理2.1 知I［S］⊆Ih(S)，考虑下面两种可能。(1)Ih(S)={u1，u2，u3，u4，u5，v1，v2，v3，v5}。如果这样，则由于v4位于v1－v3测地线上但v4∉Ih［S］，故与Ih(S)的凸性矛盾。(2)Ih(S)={u1，u2，u3，u4，u5，v1，v2，v4，v5}。如果这样，则由于v3位于v2－v4测地线上但v3∉Ih［S］，故也与Ih(S)的凸性矛盾。故这两种可能都不成立，于是Ih(S)=V，而这恰恰说明S是G的一个包集且是连通包集，由证明过程可以断定S是G的一个最小连通包集，即hc(G)=5，定理得证。

定理2.7 设G=(V，E)是一个轮图W1，r，见图6。则

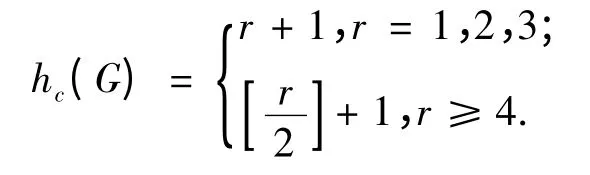
证明 若r =1，则G≌K2，则hc(G)=2;若r =2，则G≌K3，则hc(G)=3;若r =3，则G≌K4，则hc(G)=4。

图6 轮图W1，r

图7 蛛网图S1，r

定理2.8 设G(V，E)是一个蛛网图S1，r，见图7，则hc(G)=r+3。

证明 设G(V，E)是如图7 所示的蛛网图S1，r且S是G的一个最小连通包集。显然v是图G的一个极点，因此$vin S$。现在通过下面四步完成证明。

步骤1 断言:vr1，vr2，vr3这三个顶点中必有一个属于集合S。若否，则vr1，vr2，vr3这三个顶点都不属于集合S。令T=V{vr1，vr2，vr3}，则明显I［T］=T，即T是凸集，这表明S⊆I［S］⊆Ih(S)⊆T⊂V，这与S的定义矛盾。

步骤2 断言:|S|≥r+2。根据步骤1，不妨假设vr1∈S，则顶点v和vr1在子图G［S］中至少有一条路，注意到diamG(v，vr1)=r，于是|S|≥r+1。若断言不成立，则|S| =r+1，这时不得不有S={v，v11，v21，…，vr1}，故有I［S］=S，这是一个矛盾。

步骤3 断言:|S|≥r+3。根据前面两步的证明可设v，vr1∈S，如果断言不成立，则有|S| =r+2，这时易知I［S］⊆Ih(S)⊆{v，v11，v21，…，vr1，v12，v22，…，vr2}⊂V或者

根据蛛网图的一般性质可知{v，v11，v21，…，vr1，v12，v22，…，vr2}和{v，v11，v21，…，vr1，v13，v23，…，vr3}均是凸集，这是矛盾。

步骤4 完成证明。步骤3 说明hc(G)≥r+3。另一方面，容易看出集合{v，v11，v21，…，vr1，vr2，vr3}是G的一个连通包集，这意味着hc(G)=r+3，完成证明。

［1］ Tong L D. The forcing hull and forcing geodetic numbers of graphs［J］. Discrete Applied Math，2009，157:1159 －1163.

［2］ Chartrand G，Harary F，Zhang P. Geodetic Sets in Graphs［J］. Discussiones Mathematicae Graph Theory，2000，(20):129 －138.

［3］ Chartrand G，Zhang P. The forcing geodetic number of a graph［J］. Discuss Math Graph Theory，1999，19:45 －58.

［4］ Evertt M G，Seidman S B. The hull number of a graph［J］. Discrete Math，1985，57:217 －223.

［5］ John J，Mary G V. The connected hull number of a graph［J］. South Asian Journal of Mathematics，2012，2(5):512 －520.

［6］ Chartrand G，Zhang P. Introduction to Graph Theory［M］. Beijing:Posts and Telecom Press，2006.