大跨度公铁两用斜拉桥极限承载力计算方法

黄晓吉，陶晓燕

(1.华东交通大学土木建筑学院，江西 南昌 330013;2.中国铁道科学研究院 铁道建筑研究所，北京 100081)

目前国内外进行的桥梁极限承载力研究，主要分两种情况。第一种是针对某一个局部问题，如截面的拉弯极限状态、剪切极限状态、失稳极限状态或残余应力等对某种极限承载力的影响进行相应的计算研究;第二种是针对大跨度桥梁结构，考虑了非线性因素(几何非线性或材料非线性，或者二者同时考虑)而进行的大型解析计算，得到非线性相对于线性计算产生的影响及其程度;或者针对预先指定的具体部位(其它构件作为指定分析部位的背景)，考察指定部位的非线性受力状态特性。对解决桥梁结构体系的极限承载力问题，尚无直接有效的分析办法可借鉴。本文在研究分析了已有相关成果的基础上，重点对大跨度公铁两用斜拉桥结构体系的失效分析方法进行了探讨，引入了物理概念明确的、可赋予量化指标的荷载增量最小准则和阶段临界强度分枝—约界准则，解决了对结构体系进行最薄弱部位顺序失效，即失效树枝叉分析的方法［1-2］;对选定的桥梁方案进行了极限承载力的计算分析。

1 研究思路

根据失效分析方法理论，采用Ansys设计软件，首先建立计算机分析模型，计算的第一目标为求得斜拉桥4级失效对应的最小荷载增量。在分析过程中，根据应用阶段临界强度分枝—约界准则，取分枝—约界参数ck为1。具体步骤如下述。

1)施加列车荷载对结构进行整体分析，确定最不利列车加载方案。

2)施加最不利列车荷载，求算所有构件单元的荷载增量。

3)比较各杆件的荷载增量，找出最小者，即为失效单元，同时得到最小荷载增量值。

4)由最小荷载增量值修正单元有效强度。

5)处理失效单元:对于压杆失效(失稳)，则去掉压杆单元;对于拉杆失效，在拉杆单元两端施加其极限承载力的反力(等效于在下面的加载过程中，此拉杆保持具有极限承载力)，去掉拉杆单元。本文对拉杆的处理，相当于将材料视为理想弹塑性体，将超过屈服强度的部分作平直线处理。

6)重复3)—5)过程，直到找出4个失效单元，同时也得到4个最小荷载增量值。

7)将4个最小荷载增量值累加得到4级失效时最小荷载增量(为列车荷载的倍数，无量纲)，由此确定桥梁的极限承载力。

2 算例分析研究

2.1 模型分析

算例为一座(112+182+504+182+112)m公铁两用(铁路三线)桁架斜拉桥方案，主跨504 m，全长1 092 m。采用Ansys软件对该方案的实际尺寸建模并对其进行了极限承载力分析。主梁各杆件之间采用固接形式，索与主梁和桥塔之间采用铰接形式，模型的具体形式见图1。

图1 全桥计算模型

2.1.1 模型的假设与简化

由于该斜拉桥的结构复杂和计算机计算速度的限制，在整个模型的建立中作了如下的假设与简化。

1)有限元模型采用了Ansys软件提供的4种单元形式:Beam189模拟梁单元，Link10模拟索单元，采用变截面单元Beam44来模拟主塔，共划分单元约3万个。

2)桥面板与公路纵梁、上弦简化成结合梁考虑，其中混凝土的弹性模量取3.55×104MPa，钢梁的弹性模量取2.1×105MPa。

3)由于有加劲肋作构造上的保证，主梁在计算过程中不考虑翘曲应力和断面周壁的局部失稳现象。采用Von Mises屈服准则作为屈服判断法则，强化准则采用双线性随动强化。

4)所有的索一端铰接在桥塔上，另一端铰接在主梁上。对索的非线性进行简化考虑，即将其视为与它的弦长等长度的桁架直杆，通过等效弹性模量来考虑非线性的影响，索的预加力通过施加初始应变来考虑。

5)在计算分析过程中，忽略了节点板的影响，但对铁路与公路的纵横梁按实际中性轴位置输入计算坐标。

6)为简化单元，在计算分析中暂未考虑活动纵梁的作用，计算结果与实际情况相比纵梁的轴向压力较大，但对主梁其它杆件的影响较小。

2.1.2 约束与荷载

模型的具体约束情况见图1，桥塔底部约束全部自由度，桥两端及辅助墩约束UY，UZ，ROTX，ROTY4个自由度，桥塔和主梁的连接耦合了UY方向的位移，该处的主梁约束UZ，ROTX，ROTY3个自由度。

计算恒载取600 kN/m，活载按三线中—活载×0.8+6车道汽车—超20级×0.55×0.75进行考虑，计算过程中不考虑冲击系数，加载工况考虑全桥满载和仅中跨满载两种。

2.2 非线性计算原理

斜拉桥的非线性内容主要包括几何非线性及材料非线性两大部分。斜拉桥的几何非线性影响主要来自3个方面:斜索垂度的影响，主梁及桥塔的梁柱效应(或称P－Δ效应)及大位移效应(即结构坐标随变形而改变的影响)。

由于斜索存在一定的自重垂度，故其弹性模量也存在一定的下降或损失。斜索的修正弹性模量与斜索的垂度大小有关，而垂度大小又与斜索的应力和自重以及斜索的水平投影长度等有关。在大跨度斜拉桥中，考虑斜索的非线性分析一般采用Ernst公式来计算修正弹性模量［3］

式中 EI——修正弹性模量;

E0——斜索钢材的弹性模量;

γ——斜索的单位体积重量;

σ0——斜索的应力;

l——斜索的水平投影长度。

对于主梁及桥塔的梁柱效应(或称P－Δ效应)及大位移效应，在有限元分析中通过修改刚度矩阵来实现。考虑几何非线性后，采用公式(2)计算切线刚度矩阵

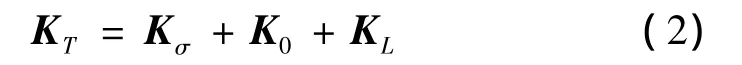
式中 Kσ——初应力或几何刚度矩阵，表示在大应变情况下初应力对结构刚度的影响，在对斜拉桥的有限元分析中代表桥塔和主梁单元的P－Δ效应;

K0——初位移或大位移刚度矩阵，表示由大位移引起的结构刚度变化;

KL——线弹性刚度矩阵。

Ansys软件提供了多种材料非线性选项。考虑斜拉桥的实际受力情况，在分析计算中对钢梁采用了理想弹塑性模型，其屈服强度取340 MPa，极限强度取370 MPa，采用Mises屈服准则，在程序中激活双线性随动强化选项。对钢筋混凝土材料和拉索采用理想弹性材料模型。

2.3 分析计算

2.3.1 索力调整

通过调整索的初始应力获得在恒载作用下的设计索力。调整33次后的索力偏差在3%以内。

计算了全桥满载和仅中跨满载两种荷载工况。当全桥满载时中跨跨中的竖向最大挠度值为66.8 cm，最大塔顶水平位移为22.8 cm，当仅中跨满载时其竖向最大挠度值为77.6 cm，最大塔顶水平位移为30.0 cm。比较这两种工况，最大竖向挠度值为77.6 cm，即挠跨比为1/649，符合文献［4］中公、铁路同时加载时竖向挠度中跨不超过1/550的规定。

2.3.3 失效分析

依据上述的计算分析结果，选取竖向挠度最大的中跨满载作为求解极限承载力的加载模式，对索、塔、梁全部构件进行了4级失效分析，失效单元位置分布见图2。

图2 失效单元位置分布

1)第一级

失效单元为382号单元，即靠近右侧边墩前一节间处的斜杆单元，受压失效。

2)第二级

杀死382号单元，对结构继续进行失效分析。失效单元为321号单元，即靠近左侧边墩后一节间处的斜杆单元，受压失效。

3)第三级

杀死321号单元，对结构继续进行失效分析。失效单元为460号单元，即靠近右侧边墩前一节间处的斜杆单元，受压失效。

2008年之前，中国实体经济的杠杆率增长相对温和，在2003年到2008年期间，由于实际GDP增长速度快于债务增长速度，中国实体经济甚至出现了自主去杠杆的过程。然而，随着2008年全球金融危机的到来，在财政政策和货币政策的双重刺激下，中国实体经济的债务快速提升，在2015年提出提出去杠杆的指导意见之前，中国实体经济杠杆率从2008年的141.2%迅速提高到2015年的227.4%，7年之间实体经济杠杆率增长了86.2%，非金融类企业的杠杆率则从95.2%增长到151.2%。

4)第四级

杀死460号单元，对结构继续进行失效分析。失效单元为399号单元，即靠近左侧边墩后一节间处的斜杆单元，受压失效。

2.3.4 失效结果分析

从以上4级失效结果可以看出，左右两侧边墩附近的斜杆是整个结构的薄弱环节。分析计算显示，在中跨满载的情况下，左右两侧边墩附近的斜杆截面是由两块1 100 mm×36 mm，和一块1 136 mm×28 mm的板组成的工形截面，其轴向压力为17 600 kN，弯矩为393 kN·m，进行偏心受压构件的检算，这4根斜杆刚刚满足稳定要求，截面基本没有富余量，最易发生失效。

最先发生失效的杆件是382号单元，即靠近右侧边墩前一节间处的斜杆单元，受压失效。当其发生失效时，最大能承受2.577 9倍铁路中—活载。当第一级失效发生以后，杆件继续承受外部荷载的能力迅速减弱，故最小荷载增量减少。

根据以上的计算结果，得出了使桥梁4级失效所需的最小荷载增量是铁路中—活载的如下倍数:2.577 9+0.007 3+0.011 9+0.014 6=2.611 7(倍)

当作用2.611 7倍铁路中—活载时，其中跨跨中竖向挠度为1.836 m，即挠跨比为1/275，桥塔的最大水平位移为68.1 cm，整个结构不能再继续承载。

3 结论

1)实例证明用最小荷载增量准则能够有效地进行结构体系失效树的分析，进而得到桥梁结构的极限承载力。

2)对(112+182+504+182+112)m跨度斜拉桥三线方案的分析表明，该结构的极限荷载为2.6117倍铁路中—活载，薄弱环节在边墩前一节间处的斜杆单元。

3)通过以上失效分析得出该桥的失效树顺序:382号单元(斜杆)→321号单元(斜杆)→460号单元(斜杆)→399号单元(斜杆)。

［1］董聪.现代结构系统可靠性理论及其应用［M］.北京:科学出版社，2001.

［2］董聪.结构系统可靠性分析的统一理论［J］.土木工程学报，2001(3):34-40.

［3］徐君兰，姚玲森.悬索桥［M］.北京:人民交通出版社，2001.

［4］中国铁路工程总公司芜湖长江大桥有限责任公司.芜湖长江大桥钢梁制造技术［M］.北京:科学出版社，2001.