基于遗传算法的C-Bézier曲线降阶

秦新强，王伟伟，胡 钢

西安理工大学 理学院，西安 710054

基于遗传算法的C-Bézier曲线降阶

秦新强，王伟伟，胡 钢

西安理工大学 理学院，西安 710054

Bézier曲线曲面是几何造型中最常用的曲线曲面之一。由于不同的CAD和CAM系统中多项式最高阶数的限制范围和要求是不同的，一方面为实现不同阶数的曲线曲面的数据转换、传递以及系统中数据存储量的压缩，另一方面为了提高计算效率和稳定性，需要对曲线曲面进行降阶处理。曲线曲面降阶的主要方法有两类：一类是基于控制顶点的几何方法。文献[1]利用升阶的逆过程来求降阶曲线的控制顶点；文献[2-4]利用扰动控制顶点和约束优化法来实现Bézier曲线曲面降阶；文献[5-6]利用Bézier曲线本身的几何性质并结合广义逆矩阵、最佳一致逼近和最小二乘理论来实现降阶逼近。另一类方法是基于基转换的代数方法。文献[7-8]利用Chebyshev多项式理论实现Bézier曲线的降阶；文献[9]利用约束Legendre多项式来进行降阶逼近；文献[10]提出了一种基于受限Jacobi多项式的Bézier曲线降阶算法。

C-Bézier曲线的应用非常广泛，在描述曲线曲面方面有重要的作用且有形状参数供设计人员选择。目前针对C-Bezier曲线，学者们已经研究了它的形状修改[11]、光顺[12]以及拼接[13]等问题，而C-Bezier曲线的降阶问题却少有涉及。文献[14]给出了基于L2范数C-Bézier曲线的最小平方逼近方法，同时考虑了C0和C1约束条件下的最小平方降阶逼近此。方法计算较繁琐，且涉及多项式方程求解问题，精度较低。为此，本文针对C-Bézier曲线的近似降阶问题，基于遗传算法的理论，提出了该曲线的一种近似降阶算法。

1 C-Bézier曲线的定义

定义1 n次C-Bézier基函数{u0，n(t)，u1，n(t)，…，un，n(t)}定义如下[15]：

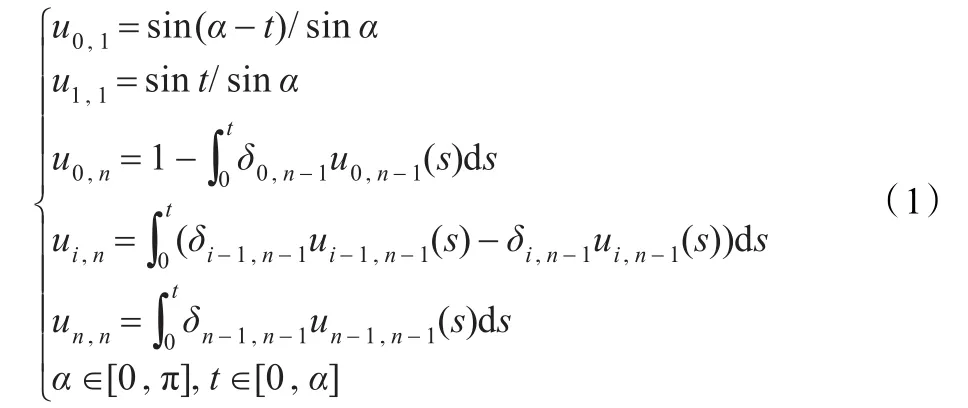
定义2由控制多边形{p0，p1，…，pn}确定的n次C-Bézier曲线为：

式中，{u0，n(t)，u1，n(t)，…，un，n(t)}为定义在空间Γn=span{1，t，…，tn-2，sint，cost}上C-Bézier基函数，α∈[0，π]为全局形状参数。

2 基于遗传算法的C-Bézier曲线降阶

2.1 降阶问题的提出

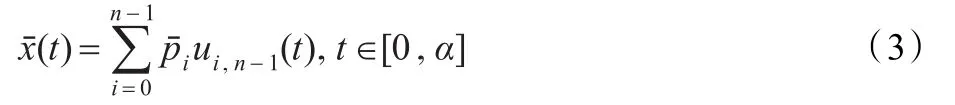
满足条件：

上述问题可以转化为如下的带约束优化问题[16]：

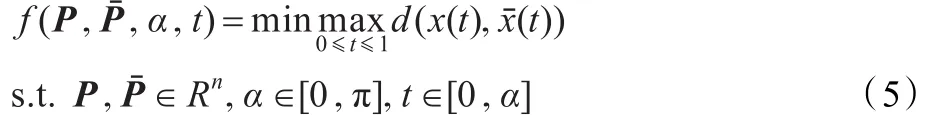
2.2 C-Bézier曲线降阶的基本思想

2.2.1 编码的表示和种群的初始化

遗传算法的一个重要步骤是对所求的问题变量实现编码，主要有二进制编码、格雷码编码、实数编码和浮点数编码。本文采用实数编码，因为对于大部分实数值优化问题采用实数编码比采用二进制编码时算法的平均效率要高。遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据，这些串结构数据的不同组合就构成了不同的点。解空间中的解数据，作为遗传算法的表现型形式。从表现型到基因型的映射称为编码。实数编码是将个体的每个基因值用某一范围内的一个实数（或浮点数）来表示，个体的编码长度等于其变量的个数。

本文群体是由降阶后C-Bézier曲线控制顶点的可行解组成。初始化种群首先要产生一个随机数αi∈[0，1]，i= 0，1，…，n-1，然后利用下式求得区间[pmin，pmax]上的控制顶点：

2.2.2 适应值函数的选取

群体的每个个体都有一个适应值，个体的性质越优，适应值越大，其繁殖下一代的可能性也就越大。为了满足C-Bézier曲线x(t)的逼近条件，所以选适应值函数为：

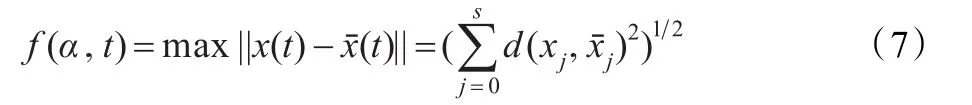
式中d(xj，xj)为Euclidean距离，α为全局形状参数，xj，(j=0，1，…，s)为降阶前后C-Bézier曲线上的点。

2.2.3 选择

选择的目的是把优良的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代，使得最优个体具有较高的复制数目。常用的方法有轮盘赌选择、随机竞争、最佳保留、无回放随机选择等。为了能保留搜索过程中的最优解，本文采用常用的转盘方法（roulette wheel selection）来进行选择。

2.2.4 杂交

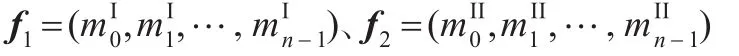
式中，βi，γi∈[0，1]的随机数。

2.2.5 变异

交叉只能对现有的基因进行排列组合，不能产生新的基因。遗传算法中的变异运算是产生新个体的辅助方法，它决定了遗传算法的局部搜索能力，同时保持种群的多样性。变异算子是对群体中染色体的某些基因值作变动。变异可使搜索跳出局部最优，是避免算法早熟的重要算子。这里采用一般的随机点对应法，即从[pmin，pmax]中选择一点，替换子解向量中对应位置的点。

2.2.6 收敛条件

遗传算法有两种终止条件：一种是确定遗传的代数，它表示遗传算法运行到指定的进化代数之后就停止运行，即已经处理完所有代群体;另一种是当在最后的一代与前一代相比没有任何的改进时，运算中止，这也表明遗传算法不再向好的方向优化，即已达到需要的误差范围。

2.2.7 控制参数的设定

在遗传法中，群体的大小、遗传运算的终止进化代数、交叉概率及变异概率四个控制参数需要预先给定。通过大量实验验证，本文采用的参数值为：80～120，180～250，0.5～0.9，0.02～0.15。

2.3 C-Bézier曲线降阶的步骤

步骤1输入降阶前的C-Bézier曲线的次数及C-Bézier曲线的控制顶点序列{P0，P1，…，Pn}。

步骤2绘制降阶前的C-Bézier曲线及其控制多边形。

步骤3初始化种群（大小为100）、控制参数（迭代次数200、交叉概率0.7、变异概率0.05）及误差（误差限数量级=取控制顶点的数据数量级/100）。

步骤4产生初始种群。

步骤5根据公式（6）计算群体的每个个体的适应值。

步骤6判断迭代次数是否小于群体代数200或每个个体的适应值是否大于给定误差，是，执行步骤7；否，执行步骤8。

步骤7进行选择杂交产生新的子代，转到步骤6，计算该个体的适应值，并进入下一代的遗传操作。

步骤8绘出降阶后的C-Bézier曲线的控制多边形及C-Bézier曲线。

2.4 实例分析

为了验证本文算法的可行性和有效性，进行大量的数值研究，以下为应用本算法的数值实例。这里参数α=2。为了估计曲线降阶的误差，本文采用式（4）、（5）的误差公式来判断降阶后曲线与待降阶曲线的x(t)之间的误差大小，其计算公式为：

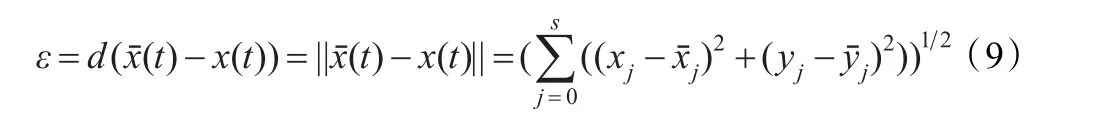
2.4.1 端点G0连续下C-Bézier曲线降阶

图1（a）给定一条三次的C-Bézier曲线，其控制顶点为{（50，0），（150，75），（250，80），（350，0）}；图1（b）给定一条三次的C-Bézier曲线，其控制顶点为{（－20，0），（5，25），（25，20），（50，0）}。

图2（a）给定一条四次的C-Bézier曲线，其控制顶点为{（50，0），（150，40），（250，60），（300，0），（350，0）}；图2（b）给定一条四次的C-Bézier曲线，其控制顶点为{（50，20），（150，40），（250，30），（300，10），（350，20）}。

2.4.2 无约束条件下C-Bézier曲线降阶

图3（a）给定一条三次的C-Bézier曲线，其控制顶点为{（50，0），（150，75），（250，80），（350，0）}；图3（b）给定一条三次的C-Bézier曲线，其控制顶点为{（50，0），（100，95），（150，80），（200，0）}。图4（a）给定一条四次的C-Bézier曲线，其控制顶点为{（50，0），（150，40），（250，60），（300，40），（350，0）}；图4（b）给定一条四次的C-Bézier曲线，其控制顶点为{（50，20），（150，40），（250，30），（300，10），（350，20）}。

图1 端点G0连续下三阶降为二阶的效果

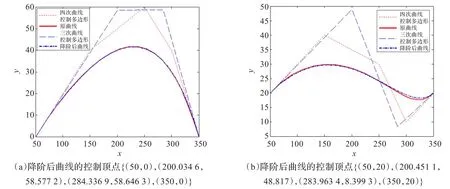
图2 端点G0连续下四阶降为三阶

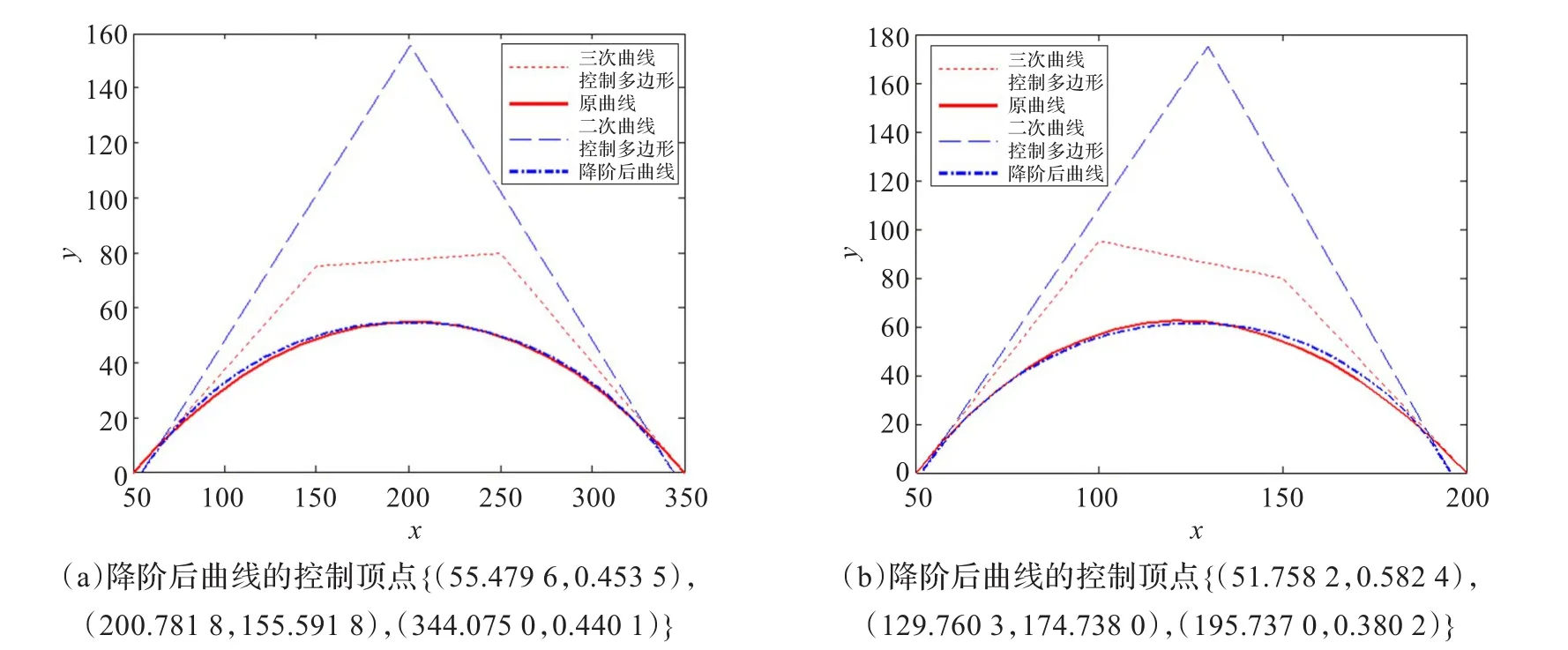
图3 无约束条件下三阶降为二阶

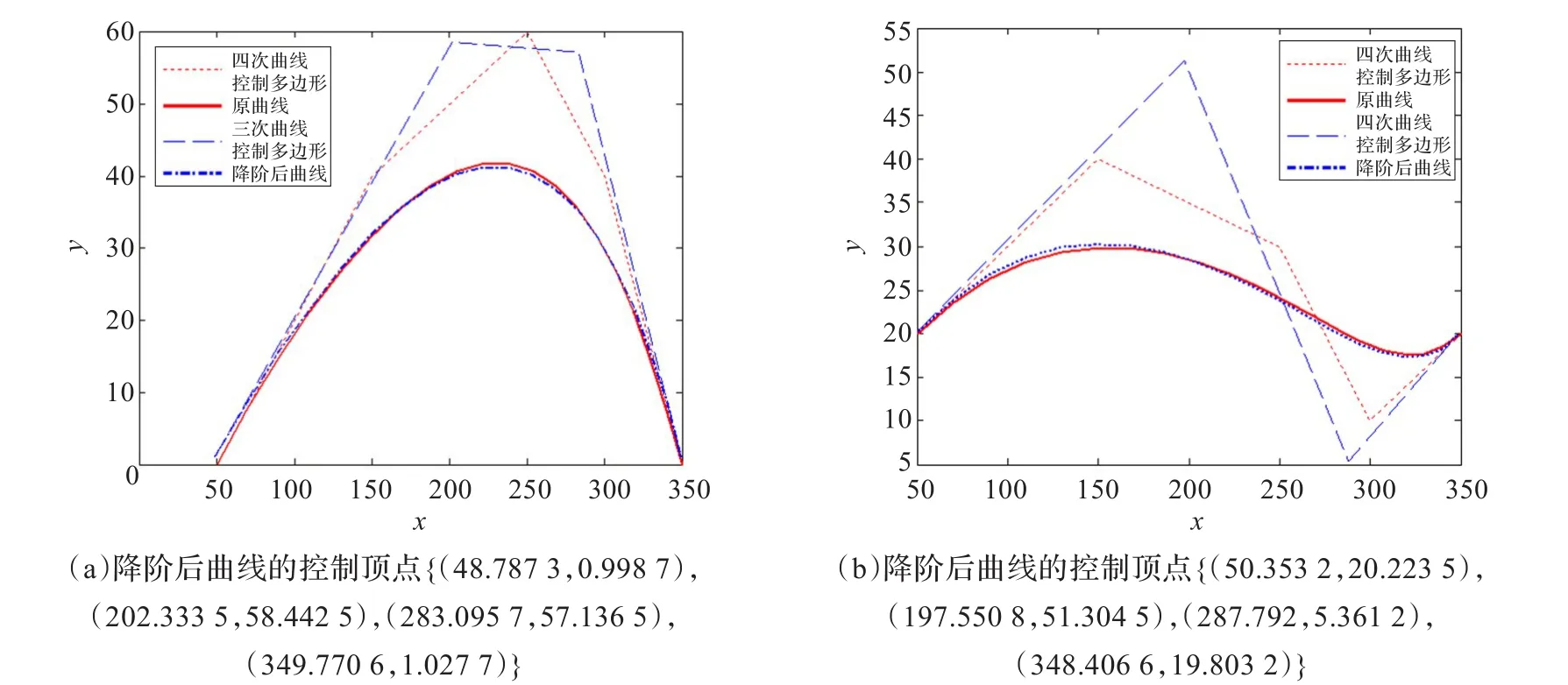
图4 无约束条件下四阶降为三阶

表1给出了在端点G0连续条件下图1、图2中实例的降阶误差；表2给出了无约束条件下图3、图4中实例的降阶误差。从表1、2中可以看出，本文方法对于C-Bézier曲线降阶的近似降阶都可获得比较小的降阶误差。这与降阶效果图的主观评价相一致，表明本文方法对于C-Bézier曲线降阶的近似降阶是相当有效的。

表1 图1和2中实例的降阶误差

表2 图3和4中实例的降阶误差

2.4.3 s取值的讨论

针对公式（7）中s该如何取值，本节作了如下的分析。利用图4（b）中的数据，当s分别取不同的值时，得到了误差ε与s的关系图，具体如图5所示。从图中可以看出，随着s的增大ε不断减小；而当s增大到一定程度之后，误差ε将不再随s值的变化而显著变化。此外，还做了大量的不同的数值实验，实验结果均表明s的值达到40～60之间时，ε不再随s的变化而显著变化。又因为s取值越大，会使得计算效率降低，所以综合考虑效率和误差两个方面的因素，在本文中取s=40。

图5 ε-s的关系示意图

2.4.4 与文献[14]做对比

为了进一步验证本文方法对C-Bézier曲线的降阶效果，用本文方法对文献[14]中例4给定的五次C-Bézier曲线进行降阶，降阶后曲线的控制顶点为{（0.093 2，－0.000 6），（－3.327 3，0.004 0），（－0.006 9，0.246 0），（3.335 8，0.004 1），（－0.094 8，－0.000 8）}，降阶误差ε=0.013 3，明显优于文献[14]方法得到的降阶误差0.069 9。本文方法的运行时间取决人为给定的遗传的终止进化代数（一般取100代），而文献[14]方法只进行一次方程组的求解，所以本文方法耗时相对较长。图6给出了两种降阶方法的对比效果，根据整条曲线降阶效果的主观评价和误差比较可知，本文方法对C-Bézier曲线的近似降级取得效果更为理想。

图6 本文方法和文献[14]方法的降阶对比

3 结束语

本文利用C-Bézier曲线的几何性质，并结合遗传算法讨论C-Bézier曲线的降阶问题，实例充分体现遗传算法在降阶过程中全局优化的特性，使得降阶曲线能很好地逼近原曲线。所提方法不仅可以获得较好的降阶效果，而且还给出了具体的降阶误差。实验结果表明本文方法在曲线设计中的有效性。

[1]任水利，张凯院，叶正麟.Bézier曲线降阶的矩阵方法[J].工程数学学报，2007，24（6）：1007-1014.

[2]Delgado J，PenaJM.Progressiveiterativeapproximation and baseswith thefastestconvergence rates[J].Computer Aided Geometric Design，2007，24（1）：10-18.

[3]Lu L Z，Wang G Z.Optimal multi-degree reduction of Bézier curves with G2-continuity[J].ComputerAided Geometric Design，2006，23（9）：673-683.

[4]陆利正，胡倩倩，汪国昭.Bézier曲线降阶的迭代算法[J].计算机辅助设计与图形学学报，2009，21（12）：1689-1693.

[5]Young J A，Byung G L，Yunbeom P.Constrained polynomial degree reduction in the L2-norm equals best weighted Euclidean approximation of Bézier coefficients[J].Computer Aided Geometric Design，2004，21（2）：181-191.

[6]Cai H J，Wang G J.Constrained approximation of rational Béziercurvesbased on a matrix expression ofitsend points continuity condition[J].Computer-Aided Design，2010，42（6）：495-504.

[7]Lu L Z，Wang G Z.Application of Chebyshev II-Bernstein basis transformations to degree reduction of Bézier curves[J]. Journal of Computational and Applied Mathematics，2008，221（1）：52-65.

[8]Rababah A，Lee B G，Yoo J.A simple matrix form for degree reduction of Bézier curves using Chebyshev-Bernstein basis transformations[J].Applied Mathematics and Computation，2006，181（1）：310-318.

[9]梁秀霞，张彩明，徐琳，等.L∞范数下使用基本曲线和修正曲线的带约束Bézier曲线降阶[J].计算机辅助设计与图形学学报，2006，18（3）：401-405.

[10]徐少平，白似雪，熊宇虹，等.在端点处保持非对称阶参数连续性的Bézier曲线降阶[J].工程图学学报，2008（5）：91-97.

[11]樊建华，张纪文，邬义杰.C-Bezier曲线的形状修改[J].软件学报，2002，13（11）：2194-2199.

[12]杨雅迪，秦新强，胡钢，等.C-Bezier曲线的光顺逼近算法[J].计算机应用，2008，28（12）：3132-3134.

[13]樊建华，邬义杰，林兴.C-Bézier曲线分割算法及G1拼接条件[J].计算机辅助设计与图形学报，2002，14（5）：421-424.

[14]王文涛.C-Bézier曲线降阶逼近[J].浙江大学学报，2009，36 （4）：396-400.

[15]Chen Q Y，Wang G Z.A class of Bézier-like curves[J]. Computer Aided Geometric Design，2003，20（1）：29-39.

[16]秦开怀，吴边，关右江，等.三维单纯性划分的遗传算法[J].中国科学：E辑，1997，27（1）：67-73.

[17]徐宗本，高勇.遗传算法过早收敛的特征分析及其预防[J].中国科学：E辑，1996，26（4）：364-375.

QIN Xinqiang,WANG Weiwei,HU Gang

School of Science,Xi'an University of Technology,Xi'an 710054,China

Aimingat C-Bézier curve of approximate degree reduction problem,a method for constructing an approximative C-Bézier curve of degree n to a C-Bézier curve of degree n+1 by genetic algorithm is provided.By means of optimization methods,degree reduction of C-Bézier curves is transformed to an optimization problem,by selecting the fitness function,using a simple loop reproduction,copy process,crossover process,mutation process,selection process obtaining the optimal value of the optimization problem to achieve C-Bézier curve endpoints in the endpoint G0unconstrained and constrained approximate reduction.The experimental results illustrate that the proposed method not only has a good merging effect,but also is easy to implement,has high precision and is simple for error estimation.

C-Bézier curve;genetic algorithm;degree reduction;least squares approximation;constraints

针对C-Bézier曲线的近似降阶问题，基于遗传算法，给出了一种用n次C-Bézier曲线最小平方逼近n+1次C-Bézier曲线的方法。该方法从最优化思想出发，把C-Bézier曲线的降阶问题转化为求解函数的优化问题，通过选择适应值函数，利用简单的循环执行复制、交叉、变异、选择求出该优化问题的最优值，从而实现了C-Bézier曲线在端点无约束和端点G0约束条件下的近似降阶逼近。实例结果表明，所提方法不仅可以获得较好的降阶效果，而且易于实现、精度高、误差计算简单，可以广泛地应用于计算机辅助设计中对曲线的近似降阶。

C-Bézier曲线；遗传算法；降阶；最小平方逼近；约束条件

A

TP391

10.3778/j.issn.1002-8331.1107-0346

QIN Xinqiang,WANG Weiwei,HU Gang.Degree reduction of C-Bézier curve based on genetic algorithm.Computer Engineering and Applications,2013,49（5）：174-178.

国家自然科学基金（No.10926152）；陕西省自然科学基金（No.2011JM1006）；陕西省教育厅自然科学研究项目（No.11JK1052）。

秦新强（1962—），男，博士，教授，主要从事计算机辅助几何设计与图形学、微分方程数值解的研究；王伟伟（1986—），男，硕士，主要从事计算机辅助几何设计与图形学的研究；胡钢（1979—），男，讲师，研究方向：计算机辅助几何设计与图形学。E-mail：xqqin@xaut.edu.cn

2011-07-18

2011-11-03

1002-8331（2013）05-0174-05

CNKI出版日期：2011-11-14 http://www.cnki.net/kcms/detail/11.2127.TP.20111114.0948.051.html