一类反应扩散方程组解的一致爆破模式

崔美英，容跃堂

（榆林学院能源工程学院，陕西榆林719000）

一类反应扩散方程组解的一致爆破模式

崔美英，容跃堂

（榆林学院能源工程学院，陕西榆林719000）

研究了一类带有非局部源的反应扩散方程组解的爆破,通过构造函数，得出解的一致爆破模式.

反应扩散方程组；一致爆破模式

1 引言

本文考虑如下带有非局部源的退化方程组解的一致爆破模式

其中Ω∈RN是有界区域,具有光滑的边界∂Ω,m,n＞1,p1, p2,q1,q2为非负常数且q1q2＞0,初始值u0(x),v0(x)是Ω上的非平凡非负连续函数.

近二十年来,很多学者都致力于研究非局部问题（参见文献[1]—[4]）,其中文献[4]中作者已经得出当p1,p2,q1,q2≥1时方程组(1)的解的整体存在性,从该文献的证明过程中我们也可以得出当m,n＞1,p1,p2,q1,q2为非负常数且q1q2＞0时方程组（1）的解也是整体存在的.关于解的爆破性质，文献[5]有如下结论：

假设有下列条件之一成立

且初值u0,v0充分大,则问题（1）的解在有限时刻爆破.并且当p1=p2=0且q1q2＞mn时，u,v同时爆破.

2 解的一致爆破模式

关于解的一致爆破模式，我们有如下定理：

定理1 当u,v爆破时，有爆破模式

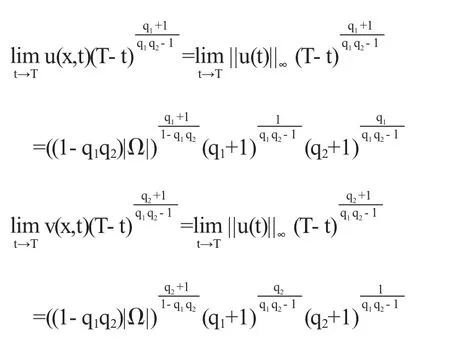
在Ω的任意紧子集上一致成立.

为了证明上述定理,我们需要作如下变换：

问题（1）就可以变成如下形式：

其中

按照文献[6]中Souplet的思想,我们定义

引理1 令(U,V)是问题(2)的一个解,如果U和V在某一有限时刻T*同时爆破,那么就有如下结论成立：

(i)在Ω×[T*/2,T*]上,存在一个常数k1≥0满足

(ii)下列两式在Ω的紧子集上一致成立：

(iii)令kρ={y∈Ω：dist(y,∂Ω)≥ρ＞0},对于任意的(x,τ)∈kρ× [T*/2,T*),都存在一个常数k2＞0满足

标注1 这个引理的证明与参考文献[7]中的引理5.2和引理5.4的证明类似,我们不再赘述.

定义1 f(t)和g(t)都是定义在[0,T)上的两个函数.如果存在常数k*≥k＞0和0＜t0＜T,满足kf(t)≤g(t)≤k*f(t),∀t∈[t0,T),那么我们称f(t)与g(t)是同阶的,记作f(t)≃g(t).如果=1或者=C（C为任一常数）,记作f(t)～g(t).

引理2 令(U,V)是问题(2)的一个解,如果U和V在某一有限时刻T*同时爆破,那么就有如下结论成立：

(i)如果p1＞0,那么

(ii)如果p2＞0,那么

(iii)如果p1=0,那么

(iv)如果p2=0,那么

证明 (i)p1＞0时p*1＞0,由引理1(i)可知

同时，从引理1(iii)中我们得知，对于所有的(x,τ)∈kρ× [T*/2,T*],都有

令τ0=max{τ1,τ3}，从(3),(4)式中我们可得

(ii)的证明与(i)类似,此处不再赘述.

(iii)根据引理1(ii)的结论,我们可以得出u(x,τ)～((1-r1)G1(τ))1/(1-r1),和V(x,τ)～((1-r2)G2(τ))1/(1-r2)在Ω的任意紧子集上一致成立,再根据勒贝格收敛定理就可以得到(τ),即引理2(iii)成立.

(iv)的证明与(iii)类似,也可以很容易得出结论.

定理1 的证明：

如果p1=p2=0,那么p*1=p*2=0,由引理2

再结合(5)式我们有

对上述的第一个式子进行积分得

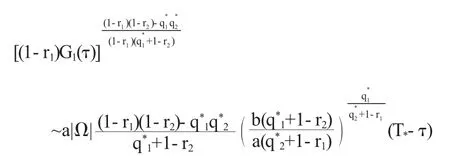
由引理1，上式可变换为

即

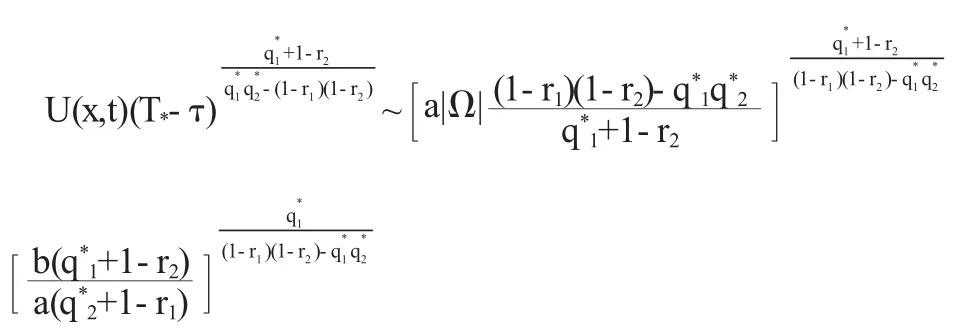
再将这部分刚开始所作的变换带入上式得到

进而得

任意紧子集上一致成立,以同样的方法可以得到v的一致爆破模式,因此定理1得证.

〔1〕Jiang L J,Li H L.Uniform blow-up profiles and boundary layer for a parabolic system w ith nonlocal sourees[J].Mathematical and Computer Modelling, 2007,45:814-824.

〔2〕孔令花,王明新.带有非局部源和非局部边界条件的抛物型方程组解的爆破性质[J].中国科学A辑:数学,2007,37 (7):817-832.

〔3〕Li F C,Xie C H.Existence and Blow2up for a Degenerate Parabolic Equation w ith Nonlocal Source[J]. Nonlinear Anal,2003,52(3):523-534.

〔4〕樊彩虹，容跃堂.一类带非局部源的反应扩散方程组解的整体存在[J].纺织高校基础科学学报，2009,22(2):172-176.

〔5〕容跃堂，崔美英.一类反映扩散方程组解的爆破[J].纺织高校基础科学学报，2011,24(4):495-498.

〔6〕Souplet P.Uniform blow up profiles and boundary behavior for diffusion equations w ith nonlocal nonlinear source[J].JDiffer Equations,1999,153:374-406.

〔7〕Du L L.Blow up for a degenerate reaction diffusion system w ith nonlinear localizde sources[J].Journal of Mathematical Analysis and Applications,2006,324:304-320.

〔8〕Chen Y P,Xie C H.Blow up for a porous medium equation w ith a localized source[J].Applied Mathematics and Computation,2004,159:79-93.

O175.29

A

1673-260X（2013）09-0001-03

榆林学院高层次人才科研启动基金项目（12GK38）