非线性方程组问题的粒子群-邻近点混合算法

张琳

陕西理工学院数学与计算机科学学院，陕西汉中 723001

非线性方程组问题的粒子群-邻近点混合算法

张琳

陕西理工学院数学与计算机科学学院，陕西汉中 723001

非线性方程组的求解问题是经典数值分析中的一类基本问题。由于传统算法涉及到函数的导数信息以及矩阵的求逆运算，使得这些算法在实际应用中有一定的局限性。

近年来，国内外学者利用智能算法求解非线性方程组取得了良好的效果。智能算法有不需要初始点以及函数导数信息等优点，因此得到很快的发展。张建科[1]用粒子群算法求解非线性方程与非线性方程组问题取得了良好效果；张安玲和刘雪英[2]给出了一种拟牛顿-粒子群混合算法；陈海霞[3]和赵晓颖等[4]把该问题转化为光滑优化问题，然后分别差分进化和粒子群算法求解取得了良好效果。另外，像蜂群[5]、鱼群等算法[6-9]也被用来求解非线性方程组问题。但这些算法大多都是依概率收敛的，并且往往需要较高的进化代数，例如文献[1，3，10]中最大进化代数为1 000代。如何有效降低算法的进化代数以提高计算速度，并且保证全局收敛或者以较高的概率收敛是一个很有意义的研究课题。

最近，周畅和张建科[11]利用粒子群和邻近点混合算法求解极小极大问题，该混合算法不但有效降低了总体进化代数，而且保证了较好的收敛性。

本文针对非线性方程组问题，在文献[11]的研究基础上进一步发展，把粒子群算法作为内层算法，外层算法采用距离函数构造邻近点算法。数值结果表明，该算法有效降低了进化算法的进化代数，收敛快、数值稳定性较好，是求解非线性方程组问题的一种有效算法。

1 非线性方程组问题

考虑如下非线性方程组：

的最优解，其中ai≤xi≤bi，cj(j=1,2,…,p)为加权系数。

单纯使用智能算法可以求解一些简单的非线性方程组问题，但往往所需进化代数较高，由于智能算法是依概率收敛的随机性算法，对一些较为复杂的此类问题，智能算法的收敛速度和收敛率都不太理想。

本文将把邻近点算法和粒子群算法相混合，发挥各自的优势，给出一种快速有效的新算法。

2 基本PSO算法

粒子群算法源于对鸟群觅食行为的研究。假设在N维的搜索空间中，有m个个体粒子组成一个种群，其中第k个个体粒子可以表示为一个N维的向量，xk=(xk1,xk2,…,xkN),i=1,2,…,m，每个个体粒子的飞行位置就是搜索空间中的一个坐标点，因而也是一个潜在的解。将xk代入需要求解的目标函数就可以算出其适应值，根据适应值的大小以及需要优化的目的（如：最大化问题还是最小化问题）可以衡量解的好坏。第k个个体粒子的飞行速度是N维向量V= (Vk1,Vk2,…,VkN)。如用Pkn=(Pk1,Pk2,…,PkN)表示第k个个体粒子迄今为止找到的最优位置，用Pgn=(Pg1,Pg2,…,PgN)来表示整个群体迄今为止找到的最优位置。

早期利用下列公式[12]对粒子个体进行操作：

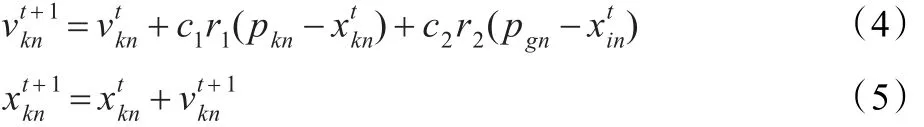
其中，k=[1,m],n=[1,N]；参数c1和c2通常称为学习因子，都是非负常数；r1和r2为相互独立的伪随机数，都服从[0，1]上的均匀分布。vkn∈[-vmax,vmax],vmax为提前设定的常数。

从式（4）、式（5）可见，c1为调节粒子飞向自身最好位置方向的步长，c2为调节粒子飞向群体的全局最好位置方向的步长。为了使粒子不会离开搜索空间，通常把vkn限定在一个范围中，即vkn∈[-vmax,vmax],vmax为最大速度，如果搜索空间在[-xmax,xmax]中，则可以设定vmax=kxmax,0.1≤k≤1.0，如果超出搜索范围，则弹回搜索空间。

Shi和Eberhart又对式（4）作了重要改进[13]：

在式（6）中ω＞0为惯性权重，控制前一速度对当前速度的影响，当ω较大时，前一速度影响较大，算法的全局搜索能力较强；当ω较小时，前一速度影响较小，算法的局部搜索能力较强。算法通过自适应调整ω大小来跳出局部最优解。算法的终止条件根据具体问题取最大迭代代数或种群搜到的最优位置满足的预定最小阈值。

3 邻近点算法

PPA（Proximal Point Algorithm）算法是由Martinet[14]在1970年提出的一种求解凸优化问题的全局收敛算法，后来Rockafellar等人[15]对该算法作了进一步的研究和发展。

对以下凸优化问题：

这里f:Rn+m→(-∞,+∞]是一个闭正则凸函数。约束凸优化问题包含于式（7）中，因为可以利用示性函数δC(•)把约束优化转化为无约束优化问题。转化方法如下：

如果f0(x,y):Rn+m→R为有约束优化问题的目标函数，该问题的可行域C={(x,y)|gi(x,y)≤0,i-1,…,p}为Rn+m中的闭凸集，每个约束函数gi(x,y)是可行域上的闭凸函数，则

因此，式（8）可化为式（7）。

采用PPA求解式（7），其迭代点列{(xk,yk)}计算如下：

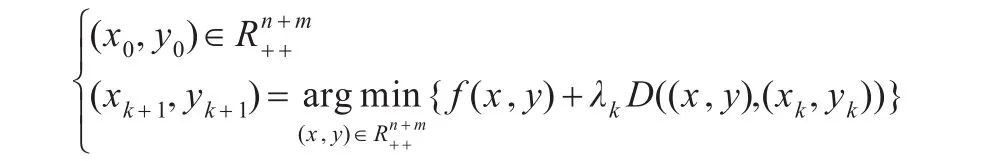
其中D(·,·)是一个类似距离函数，早期的邻近点算法采用经典的欧几里德距离函数来，很多满足凸性的类似距离函数被提出来，例如：Bregman函数、类似熵函数等等。

PPA算法是一个经典确定性算法，如果优化问题是凸优化问题，则由该算法产生的点列{(xk,yk)}收敛于全局最优点，该结论在很多经典文献中都已证明过，可参见文献[14-16]等文献。

4 粒子群-邻近点混合算法

以下结合邻近点算法给出一种非线性方程组问题的改进粒子群算法。

4.1 PSO-PPA算法步骤

步骤1调用PSO算法计算非线性方程组问题得到初始迭代点x0。

步骤2给定正数λk＞0，置k：=2。

步骤3调用PSO算法求解邻近点迭代问题，得到xk+1。

步骤4检验是否达到精度要求，若是，算法停止；否则，k：=k+1，转步骤3。

4.2 内层PSO算法

步骤1初始化一个规模为N的粒子群，随机产生每一个粒子的初始位置和速度。

步骤2计算每个粒子的适应值，对问题式（1），其适应值函数为：，此处的距离函数也可以使用Bregman函数、类似熵函数等其他距离函数。

步骤3对每个粒子将其适应值和其经历过的最好位置Pij的适应值进行比较，若较好，则将其作为当前的最好位置。

步骤4对每个粒子将其适应值和全局经历过的最好位置Pgj的适应值进行比较，若较好，则将其作为当前的全局最好位置。

表1 计算结果比较

步骤5根据式（6），式（5）分别对粒子的速度和位置进行更新。

步骤6如果满足终止条件，则输出解；否则返回步骤2。

4.3 必要的说明

（1）如果式（1）中的各个分量gi(x),i=1,2,…,p都是凸函数，则转化后的优化问题式（3）也是一个无约束凸优化问题。因此，用邻近点算法为外层算法可以保证迭代点列收敛到全局最优解。

（2）对于比较复杂的非线性方程组问题，如果式（1）中的某个分量gi(x),i=1,2,…,p不是凸函数，则问题式（3）也是一个非凸优化问题。尽管如此，本文中算法也可以求解，但此时的收敛性理论分析以及计算精度有待进一步更深入研究。

5 数值结果

为验证本文算法的性能，取相关文献中三个非线性方程组问题做测试，并和文献中结果比较。

在此选取学习因子c1=c2=2,ω从1.0减小到0.4，群体规模数为20，内循环最大进化代数为100，λk=0.5，粒子的搜索范围根据具体问题定。在硬件环境：CPU：Pentium4 2.93 GHz、内存：512 MB等和软件环境WindowsXP系统下用VC++6.0编程运行。外循环迭代次数为5次，内循环算法运行PSO 20次，每次从中选取适应值最差的粒子的位置作为下一次迭代的初始点。由于例2中fi(x)(i=1,2,3)都是非负的，因此直接最小化∑ifi(x)。计算结果见表1。

数据分析：本文列出了外层迭代5次，内循环PSO的最大进化代数100代，搜到的最差解和其他文献中结果比较如表1所示。由于最大进化代数和搜索成功率密切相关，因此在表1中列出了最大进化代数，而没有列出平均进化代数。由表1可以看出，PSO-PPA算法对例1和例2需要较少的迭代步就可以达到10-9的精度，而且可保证对凸问题的100%全局收敛性。这是单纯依靠概率收敛的进化算法所达不到的。对例3的计算精度没有HPSO高，但本文算法具有确定的收敛特性。可见，本文算法综合了PPA和PSO的各自优势，即不需要初始点和函数可微性要求，对凸问题具有全局收敛性，是一种较好的混合算法。

但是，由于目前只证明了PPA算法对拟凸问题[16]具有全局收敛性。因此，混合算法对非拟凸问题，没有全局收敛性理论结果，计算效果也不一定好。关于这一点，还需深入研究。

6 结论

本文针对非线性方程组问题，利用粒子群算法结合邻近点算法给出了此类问题的一种新的混合有效算法，该算法无需使用导数信息。并能快速搜到问题的解。

该算法不但给非线性方程组问题提供了一种新方法，而且拓广了粒子群算法的应用范围。数值结果表明，该算法收敛快、数值稳定性好，是求解非线性方程组问题的一种有效算法。

[1]张建科，王晓智，刘三阳，等.求解非线性方程及方程组的粒子群算法[J].计算机工程与应用，2006，42（7）：56-58.

[2]张安玲，刘雪英.求解非线性方程组的拟牛顿-粒子群混合算法[J].计算机工程与应用，2008，44（33）：41-42.

[3]陈海霞，杨铁贵.基于极大熵差分进化混合算法求解非线性方程组[J].计算机应用研究，2010，27（6）：2028-2030.

[4]赵晓颖，刘国志，姜凤利.求解一类不可微优化问题极大熵微粒群混合算法[J].江西师范大学学报：自然科学版，2007，31（2）：193-196.

[5]张姣玲.求解非线性方程及方程组的人工蜂群算法[J].计算机工程与应用，2012，48（22）：45-47.

[6]刘大平，何平.区间-粒子群算法求解非线性方程组[J].内江师范学院学报，2010（12）：21-23.

[7]陈海霞，杨铁贵.基于凝聚函数法的非线性方程组求解[J].科学技术与工程，2010（6）：1494-1496.

[8]王冬冬，周永权.人工鱼群算法在求解非线性方程组中的应用[J].计算机应用研究，2007，24（6）：242-244.

[9]莫愿斌，陈德钊，胡上序.求解非线性方程组的混沌粒子群算法及应用[J].计算力学学报，2007，24（4）：505-508.

[10]欧阳艾嘉，刘利斌，乐光学，等.求解非线性方程组的混合粒子群算法[J].计算机工程与应用，2011，47（9）：33-36.

[11]周畅，张建科.一类非线性极小极大问题的粒子群-邻近点算法[J].计算机工程与应用，2012，48（36）：19-22.

[12]Kennedy J，Eberhart R.Particle Swarm Optimization[C]//Proc IEEE Int Conf Neural Networks.Piscataway：IEEE Press，1995：1942-1948.

[13]Shi Y，Eberhart R.A modified Particle Swarm Optimizer[C]// Proceedings of the IEEE International Conference on Evolutionary Computation.Piscataway，NJ：IEEE Press，1998：69-73.

[14]Martinet B.Regularisation d’inequations variationnelles par approximations successives[J].RIRO，1970，4：154-159.

[15]Rockafellar R T.Monotone operators and the proximal point algorithm[J].SIAMJournal on Control and Optimization，1976，14：877-898.

[16]Langenberg N，Tichatschke R.Interior proximal methods for quasiconvex optimization[J].Journal of Global Optimization，2012，52（3）：641-661.

ZHANG Lin

School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong,Shaanxi 723001,China

The problems of nonlinear equations are a class of classical numerical calculation problems,and the simple evolutionary algorithm requires not only a high degree of evolution algebra,but also can not 100%guarantee to converge to the global optimal solution.To solve this problem,Particle Swarm Optimization and Proximal Point Algorithm are mixed,and the Proximal Point Algorithm is used as the outer layer algorithm,and the Particle Swarm Optimization is used as the inner layer algorithm to solve the problems of nonlinear equations.The algorithm has better effects of computation for convex problems,which is an effective algorithm of solving nonlinear equations.

Particle Swarm Optimization（PSO）;Proximal Point Algorithm（PPA）;systems of nonlinear equations

非线性方程组问题是一类经典的数值计算问题，单纯的进化算法不但需要很高的进化代数，而且也不能保证100%收敛到全局最优解。为求解此问题，把粒子群算法和邻近点算法相混合，利用邻近点算法作为外层算法，粒子群算法作为内层算法进行求解。实验结果表明该算法对凸问题有较好的计算效果，是求解非线性方程组问题的一种有效算法。

粒子群算法；邻近点算法；非线性方程组问题

A

TP18

10.3778/j.issn.1002-8331.1306-0355

ZHANG Lin.Particle Swarm Optimization-Proximal Point Algorithm for systems of nonlinear equations.Computer Engineering and Applications,2013,49（24）：38-40.

陕西理工学院科研基金资助项目（No.SLGJX1025）。

张琳（1964—），男，副高，主要研究方向：应用数学。

2013-07-01

2013-08-22

1002-8331（2013）24-0038-03

CNKI出版日期：2013-10-17http://www.cnki.net/kcms/detail/11.2127.TP.20131017.1529.013.html