计算空间点到细分曲面有符号最近距离的方法

朱建宁，王敏杰，魏兆成，曹 斌

（大连理工大学 机械工程学院，辽宁 大连 116024）

0 引言

细分曲面建模方法不仅具有非均匀有理B样条（Non－Uniform Rational B－Spline，NURBS）方法的局部性和仿射不变性等良好性质，还具有NURBS方法所不具有的拓扑任意性和整体连续性，可以构造具有任意拓扑结构的光滑曲面，因此广泛应用于影视、动画和虚拟现实等领域。然而，细分曲面建模方法中存在的一些关键问题成为细分曲面在工业领域应用的瓶颈，其中计算空间点到细分曲面有符号最近距离就是一个重要的问题。同时，在机器人运动规划和数控加工等领域，空间点到细分曲面有符号最近距离也是解决物体间运动干涉和碰撞检测问题的基础。

有关计算点到参数曲面最近距离的研究比较广泛，徐汝锋等［1］首先在参数曲面上选取一个初始点，以该点为中心点，按给定步长求取周围的四个顶点，在上述五个顶点中，将距离空间点最近的顶点作为中心点，步长减半再次求取其周围的四个顶点，重复以上步骤，直到获得满足一定精度的最近距离。熊志刚等［2］采用双向黄金分割法对参数曲面的参数空间进行分割，通过计算和比较黄金分割点函数值，逐次缩小参数区间。当参数区间缩小到一定程度时，以空间点到黄金分割点的最近距离作为近似最优解。苏智剑等［3］利用遗传算法计算空间点到参数曲面的最近距离，首先将参数曲面离散成空间点，然后采用遗传优化方法初步判断问题解所在的区间，最后采用连续变量优化方法求得问题的精确解。廖平［4］利用粒子群优化算法计算空间点到参数曲面的最近距离，理论上能够获得全局最优解，但计算速度较慢。由于细分曲面没有整体的解析表达式，上述研究方法不能直接应用于空间点到细分曲面最近距离的计算，在实际应用中，常常采用一定细分次数的控制网格代替细分曲面进行各种几何操作。关于计算点到网格模型最近距离的研究，方向等［5］提出一个快速计算空间点到任意多面体的有符号距离的方法，该方法以空间点为中心，采用动态球搜索技术，通过缩小三角面片的搜索范围来提高搜索距离空间点最近的三角面片的搜索效率。但是细分曲面不同于一般的网格模型，为表示复杂形体的光滑曲面，细分曲面控制网格的数据量十分巨大，一般搜索技术的效率难以满足应用。目前，仅有TorstenUllrich等［6］对计算空间点到 Catmull－Clark［7］细分曲面的最近距离问题进行了研究。该研究通过将Catmull－Clark细分曲面离散成三角面片，以空间点到三角面片的最近距离作为空间点到细分曲面的最近距离；利用细分曲面分片表示和自适应细分技术，使细分曲面的数据存储和三角面片的数量减少到最低；通过建立Catmull－Clark细分曲面的距离场，提高了搜索三角面片的效率。然而，通过自适应细分技术减少的三角面片数量有限，且容易产生数值误差，同时建立距离场的代价也比较高。

为解决以上问题，本文以Catmull－Clark细分曲面为例，研究快速计算空间点到细分曲面最近距离的方法。本文采用一定细分层次的极限网格表示细分曲面，以空间点到极限网格顶点的最近距离作为空间点到细分曲面的最近距离。通过改进的Catmull－Clark细分曲面数据结构，能够更好地实现细分曲面的分片表示，进而采用分治策略和包围体技术缩小极限网格顶点的搜索范围，而且采用较粗层次控制网格创建包围体的代价要比建立距离场的代价低。根据细分曲面面片拓扑结构的特性创建多分辨率采样技术，基于该技术可以显著提高搜索最近顶点的效率。本文算法将计算空间点到细分曲面面片和空间点到细分曲面整体的最近距离问题有机地统一起来，是一种理想的全局寻优算法。

1 算法原理

当细分曲面表示精度较高时，网格顶点的密度非常大，空间点到三角面片顶点的最近距离与空间点到三角面片的最近距离相差较小，而计算点与点的距离要比计算点与三角面片的距离更加稳定和快速。因此，可以将计算空间点到细分曲面的最近距离问题转化为搜索距离空间点最近的细分曲面网格顶点问题。首先，创建一个数据结构，实现细分曲面的分片表示，进而采用分治策略，将在细分曲面全局范围内搜索最近顶点的问题转化为在各个细分曲面面片（Subdivision Surface Patch，SSP）局部范围内搜索最近顶点的问题，搜索结果的全局最优解理论上存在于局部最优解中。然后，利用细分曲面控制网格的凸包性质对每个SSP构建包围体；计算空间点和包围体之间的最近距离Dpb，将SSP按照该距离由小到大进行排序，以此顺序分别计算空间点与SSP的最近距离Dpssp。将逐次计算得到的Dpssp进行比较，获得准全局最近距离Dminq。在每次计算之前，对比Dpb和Dminq的大小，如果Dpb≥Dminq，则停止计算，该Dminq即为空间点到细分曲面的最近距离Dmin；否则继续计算，直到获得Dmin为止。

在徐汝锋［1］和熊志刚［2］等的研究中，分别以不同的方式实现了参数曲面采样。通过采样点择优与采样区域缩小的交替进行，完成了最近顶点的搜索；在计算空间点到SSP最近距离的研究中，利用SSP网格的拓扑结构特性，发展了文献［1－2］的理论；根据SSP网格的拓扑结构特性，制定多分辨率采样规则；以相对较低层次的网格顶点作为低分辨率采样点，以相对较高层次的网格顶点作为高分辨率采样点；通过择优的低分辨率采样点确定再次进行高分辨率采样的区域，重复此过程一定次数，就可以最终锁定距离空间点最近的SSP网格顶点，此顶点与空间点的距离即为Dpssp；根据此顶点的坐标和法向建立参数直线方程，计算直线中距离空间点最近的参数点；以参数点与空间点的距离为基础，对计算结果进行误差分析，如果计算结果没有满足误差要求，则结合局部细分技术，对SSP局部进行高分辨率采样，再次计算最小距离，直到计算结果满足误差要求为止；最后，以参数点的参数值确定Dpssp的符号。

2 算法描述

2．1 细分曲面生成

2．1．1 细分次数

细分曲面是控制网格不断细分的极限状态。在实际应用中，通常用一定细分次数的控制网格代替细分曲面。理论上，细分次数越高，控制网格的表示精度越高，使细分曲面的数据量呈指数速率增长，给细分曲面应用于高精度的工业领域增加了困难。因此，一些学者［8－10］对控制网格与细分曲面之间的误差分析以及细分次数与表示精度的映射关系进行了深入研究。极限网格和控制网格具有相同的拓扑结构，极限网格顶点是控制网格对应顶点的极限位置。对于逼近型细分曲面，相同细分次数的极限网格比控制网格具有更高的表示精度。本文应用Catmull－Clark细分曲面极限网格计算空间点到Catmull－Clark细分曲面的最近距离，采用Huang等［11］的方法确定Catmull－Clark细分曲面极限网格的细分次数。

2．1．2 数据结构

数据结构是细分曲面实现和应用算法开发的基础。目前，细分曲面常用的数据结构分别为基于边［12］和四叉树［13］结构，这两种数据结构在细分次数较高时，不但十分消耗计算机内存，而且搜索和查询的效率较低。Settgast等［14］在进行 Catmull－Clark细分曲面自适应细分的研究中，为解决细分曲面内存消耗过大的问题，提出用二维数组分片表示细分曲面的方法。但Settgast的做法有两个缺陷：①规则的二维数组不能很好地表示SSP周围不规则的邻域结构，不利于细分算法实现及数据结构在多种细分模式中推广；②二维数组中过多的邻域结构信息不利于细分曲面应用算法的开发。

本文构建了一个双层数据结构，来更好地表示Catmull－Clark细分曲面，将该数据结构命名为元胞数据结构。内层数据结构主要包含一个二维数组和若干个一维数组，其中二维数组只表示SSP的信息，将其命名为元胞数组Ac，Ac＝（2N＋1）2，N为细分次数。若干个一维数组用来表示SSP的邻域结构信息，这些邻域结构信息主要辅助SSP进行细分，分为两类：①辅助SSP的“角点”进行细分，将其命名为辅助角点细分结构Av，Av＝2Ne＋1，Ne为“角点”的价；②辅助SSP的“边界”进行细分，将其命名为辅助边界细分结构Ab，Ab＝2N＋1。外层数据结构可以采用半边数据结构，通过细分曲面初始网格的拓扑结构来表达SSP之间的拓扑关系。图1所示为SSP（顶点V1，V2，V3和V4组成）创建的元胞数据结构示意图。

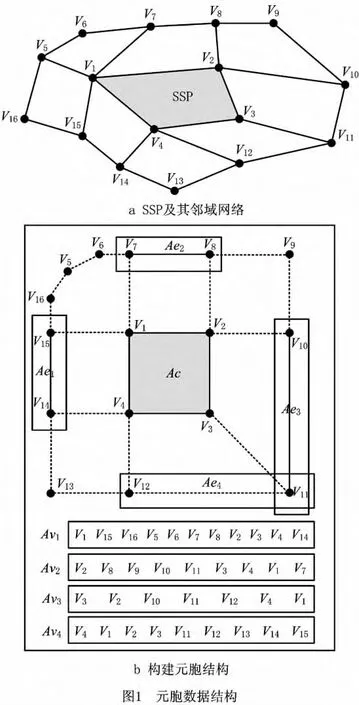
2．1．3 细分算法实现

应用元胞数据结构，可以将Catmull－Clark细分曲面的整体更新转化为各个元胞的局部更新，每个元胞的更新主要分为Ac的更新和辅助细分结构的更新两方面。Ac的更新分为三部分：①Ac“角点”的更新，由Av完成；②Ac“边界”的更新，由Ab和Ac的边界部分共同完成；③Ac内部的更新，Ac的信息就可完成该部分的更新。辅助细分结构的更新分为两部分：①Av的更新，由Av独自完成；②Ab的更新，由Ab和Ac的边界部分共同完成。图2所示为Catmull－Clark细分曲面元胞数据结构的更新示意图。极限网格同样可以应用元胞数据结构进行分片表示。当细分N次的控制网格计算完成后，可以进行细分N次的极限网格的计算。细分N次的极限网格顶点位置和法向的计算过程与细分N＋1次控制网格新顶点的计算过程类似，具有相同的控制网格顶点搜索策略，仅仅是计算过程中控制网格顶点的加权系数不同。

2．2 分治策略与包围体

2．2．1 分治策略

元胞数据结构的数据元素是由Ac表示的SSP，这为分治策略的实施提供了基础。计算空间点到细分曲面最近距离的关键，是快速、准确地搜索距离空间点最近的网格顶点，采用分治策略是为了提高搜索的效率。通过分治策略，将细分曲面整体范围内的搜索划分为有限个SSP范围内的搜索。对每个SSP构建包围体并计算空间点和包围体的最近距离，确定优先计算最近距离的SSP。当未搜索SSP的包围体与空间点的最近距离大于当前最优结果时停止搜索，从而提高搜索的效率。

2．2．2 包围体

包围体的基本思想是使用体积略大而几何特征简单的几何体（球体、长方体等）来近似表示复杂的几何对象。目前，常用的包围体有包围球、轴向包围盒、固定方向包围盒、方向包围盒和离散方向包围盒等。为方便计算空间点到包围体的最近距离，本文采用包围球来近似表示SSP。对于逼近型细分模式，可以根据控制网格的凸包性质构建包围球。为提高构建包围球的效率，可以采用较低层次的控制网格顶点构建包围球，构建方法如下：

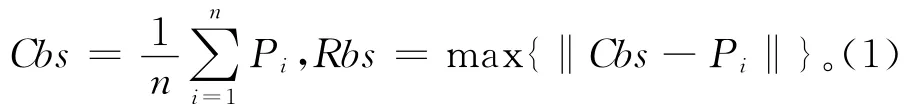
式中：Cbs表示包围球的球心点，Rbs表示包围球的半径，P1，P2，…，Pn表示控制网格顶点。

2．2．3 计算空间点与包围球的最近距离

设空间点到包围球的最近距离为Dpb，

式中Dpc表示空间点到包围球球心的距离。当计算结果为负值时，说明空间点在包围球的内部。将SSP按照其Dpb由小到大进行排序，以该顺序开始计算空间点到SSP的有符号最近距离。

2．3 计算空间点到SSP的有符号最近距离

2．3．1 搜索策略

细分曲面通过多边形网格表示造型曲面。细分曲面的极限网格不断加密逼近造型曲面，每次细分增加的极限网格顶点可以认为是对极限曲面的高分辨率采样。利用递归细分过程中极限网格由粗到精的特性，扩展了文献［1－2］的搜索策略。具体的搜索策略如下：当Catmull－Clark细分曲面面片进行第一次细分后，搜索区域被自然地分割为四个子区域。第二次细分后，每个子区域内生成对应的采样点，锁定距离空间点最近的采样点的子区域。再次细分后，锁定的子区域被分割为四个区域，且每个区域中都生成一个采样点。每次细分完成后都伴随着采样点择优和搜索区域分割的过程。当最后一次细分完成后，对锁定搜索区域内的所有顶点进行采样，选取距离空间点最近的顶点。

2．3．2 多分辨率采样

上述搜索策略中所需要的采样点，可以通过多分辨率采样技术从极限网格中获取。对于SSP，极限网格顶点的数值存储在对应的元胞数组Ac中，Ac的行列索引实现了SSP的自然参数化。不同细分层次极限网格顶点的行列索引遵循如下定理和推论：

定理1 对于细分次数为N的Catmull－Clark细分曲面面片，Ac＝（2N＋1）2。在该Ac中，以2N－m为索引间距，提取第m次细分（m≤N）的极限网格顶点。

推论1 第m1次细分与第m2次细分（m1＜m2）的极限网格顶点的索引间距为（2N－m1－2N－m2）。

推论2 相邻细分层次（m2－m1＝1）的极限网格顶点索引间距为2N－m2。

基于上述定理与推论，在SSP中搜索对应的顶点，可以实现SSP的多分辨率采样。具体做法是在第二次细分的极限网格中提取初始的四个采样点，分别为：

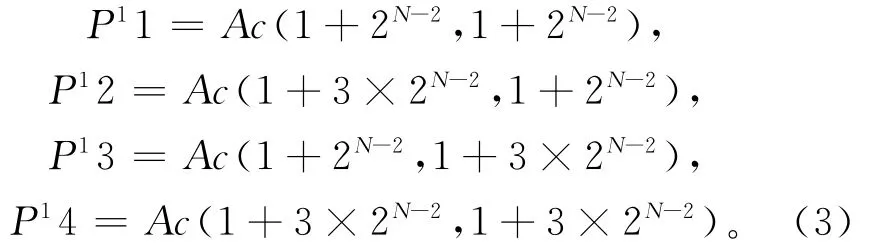
式中：P11，P12，P13和P14分别表示初始的四个采样点，N为细分次数。将四个采样点中距离空间点最近的点设为择优点，择优点所在的区域即为下次采样的区域。择优点的表达式为

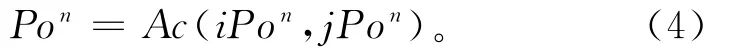
式中：Pon表示第n次搜索时的择优点，iPon和jPon分别表示择优点的行列索引值。从第二次到第N－1次获得采样点的过程，可以用如下关系表示：

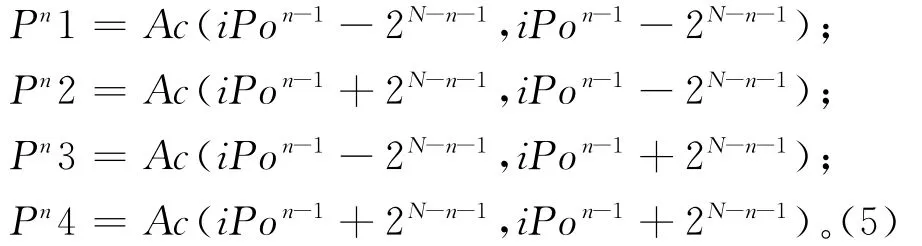
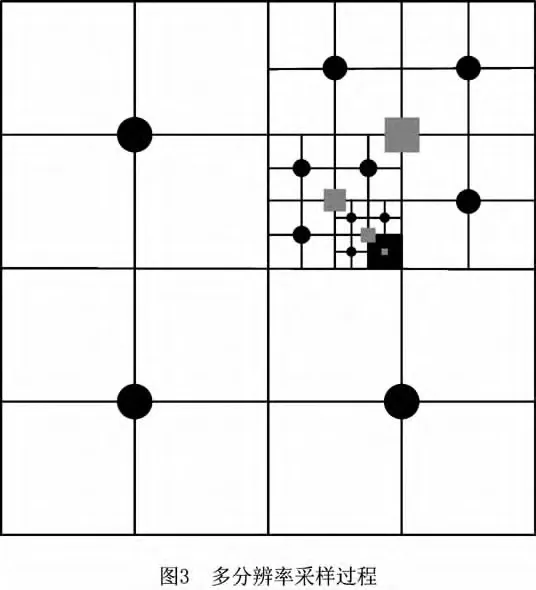
式中：Pn1，Pn2，Pn3和Pn4分别表示第n次搜索的四个采样点，iPon－1和jPon－1分别表示第n－1次择优点的行列索引值。第N次采样点由PoN－1的1－邻域顶点构成，从中选取距离空间点最近的顶点。应用多分辨率采样技术，在细分五次的SSP中搜索最近点的过程如图3所示，圆形点为每次的多分辨率采样点，方形点为择优点，最近点在图中的深色区域顶点中择优获得。

2．3．3 最近距离的误差分析与符号判断

以搜索的最近顶点的位置和法向建立参数直线方程，

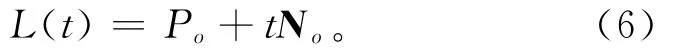
式中：Po表示最近顶点的位置；No表示最近顶点的法向，可由Halstead等［15］的极限点法向公式计算。建立如下空间点与直线上参数点的距离表达式：

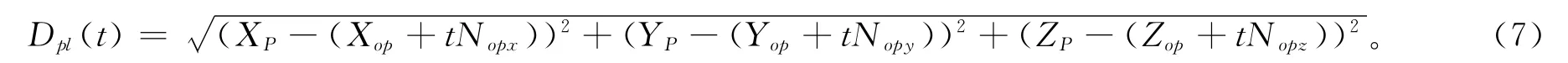
式中：Dpl（t）表示空间点与直线上参数点的距离，XP，YP和ZP分别表示空间点的坐标分量，Xop，Yop和Zop分别表示最近顶点的坐标分量，Nopx，Nopy和Nopz分别表示最近顶点法向的分量。令a＝Xp－，可以证明当参数时，Dpl（T）的值最小，最小值

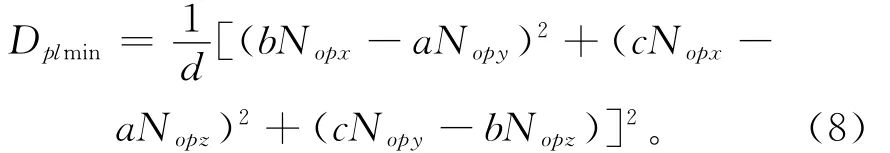
以Dpop表示空间点和最近顶点的距离，设精度评价系数，当λ值足够小时，认为计算结果满足精度要求。通过参数T的正负来判别最近距离的符号，当T＞0时，说明空间点在细分曲面的外部，则最近距离符号取为正；当T＜0时，说明空间点在细分曲面的内部，则最近距离符号取为负。

2．3．4 算法描述

下面以Catmull－Clark细分曲面为例，描述计算空间点到Catmull－Clark细分曲面面片有符号最近距离的算法。

步骤1 提取采样点P11，P12，P13和P14。

步骤2 分别计算空间点到P11，P12，P13和P14的距离。

步骤3 根据择优采样点和索引间距提取采样点P21，P22，P23和P24。

步骤4 交替进行采样点择优和搜索区域分割，直到确定第N－1次的择优采样点PoN－1。

步骤5 在PoN－1的1－邻域点中确定距离空间点最近的顶点。

步骤6 以最近顶点的位置和法向建立参数直线方程，以此为基础对计算结果进行误差分析。若计算结果没有满足精度要求，则对相应区域进行局部细分，然后返回步骤4，直到所得计算结果满足精度要求。

步骤7 根据参数T判别Dpssp的符号。

2．4 计算空间点到细分曲面有符号最近距离的算法描述

下面以Catmull－Clark细分曲面为例，描述计算空间点到Catmull－Clark细分曲面有符号最近距离的算法。

步骤1 根据细分曲面表示精度确定极限网格的细分次数。

步骤2 应用元胞数据结构生成极限网格。

步骤3 对每个SSP构建包围球。

步骤4 计算Dpb，并以此距离对SSP的排序。

步骤5 逐次计算空间点到排序SSP的最近距离。如果Dpb≥Dminp，则停止计算，该Dminp即为空间点到细分曲面的最近距离；否则继续计算，直到获得Dmin为止。

3 算法测试及讨论

上 述 算 法 在 Pentium （R）Dual－Core CPU E5200 2．5GHz、1G 内存的硬 件平 台上，应 用MATLAB 7．10．0软件实现，并进行实例测试。

3．1 计算空间点到SSP有符号最近距离

本部分主要测试算法的计算精度。理论上，如果距离空间点的最近点存在于曲面的内部，则空间点应该在最近点的法线上。如图4所示，测试模型是细分10次的Catmull－Clark细分曲面面片的极限网格。在该SSP中，均匀采样25个顶点，将采样点沿其法矢的正向和反向分别等距，把获得的50个等距顶点作为此部分算法测试的测试点。如果等距测试点的最近点搜索结果为其对应的采样点，则说明该算法的搜索结果是准确的。如表1所示，50个测试点搜索最近顶点的准确率为100%，这说明测试点不论在曲面的“内部”还是“外部”，算法都能准确搜索到空间点的最近顶点。在测试模型的顶点数目达到百万级的情况下，单次测试平均耗时仅为0．228ms，测试结果也表明算法的搜索速度较快。

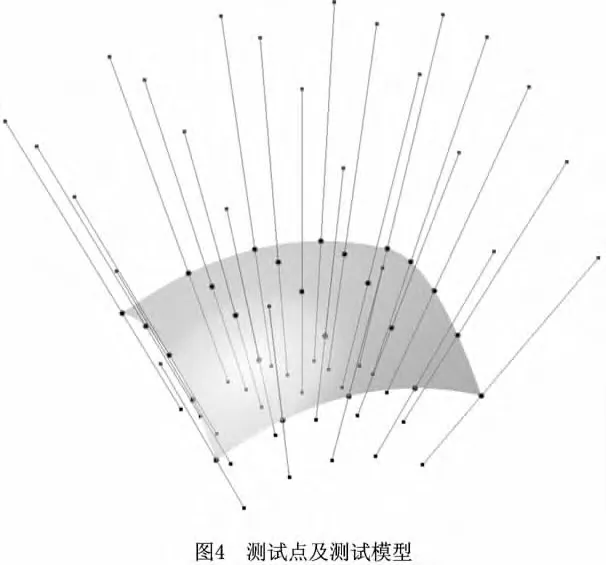
表1 计算50个测试点到SSP最近距离的测试结果

3．2 计算空间点到Catmull－Clark细分曲面有符号最近距离

本部分主要测试算法的计算效率。如图5所示，测试模型是细分9次的Catmull－Clark细分曲面的极限网格，模型共有196片SSP。图5中的散乱点（由圆点表示）为该部分算法测试的测试点。测试指标分别为：搜索最近顶点所涉及的SSP个数，计算最近距离的耗时及最近距离的数值、误差因子和距离符号。从测试结果可以看出，误差因子的数值都非常小，可以认为计算结果满足精度要求，同时算法也能正确判断出最近距离的符号。如图6所示，计算耗时与算法需要搜索的SSP个数呈线性关系。分治策略的实施使搜索SSP的个数只占测试模型SSP总数的一小部分，降低了算法的计算规模。同时，对于细分次数为N的SSP，计算空间点到SSP的最近距离仅需要搜索4 N＋4个网格顶点即可完成。如表2所示，在测试模型的顶点数目达到千万级的情况下，计算耗时仍很小。其中，最大耗时为0．626ms，最小耗时仅为0．129ms。测试结果表明算法的计算效率较高。

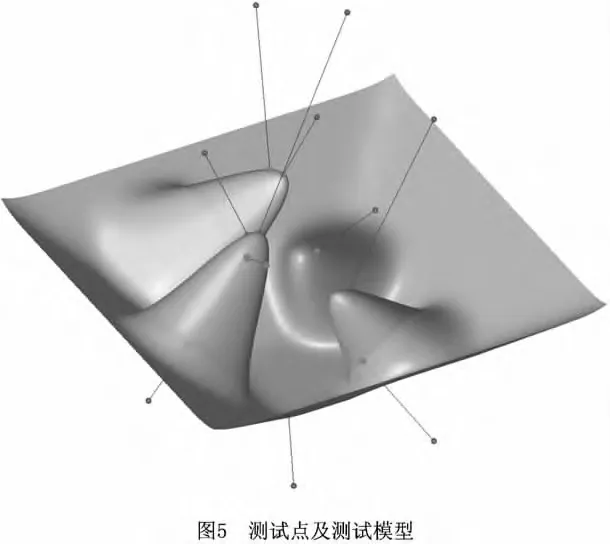
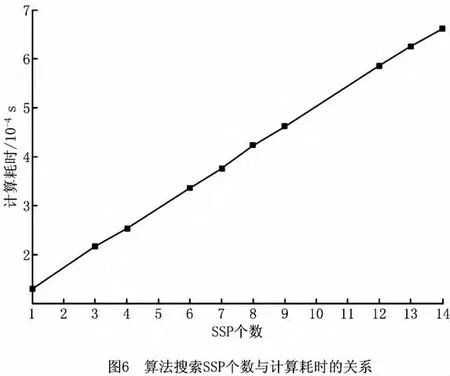
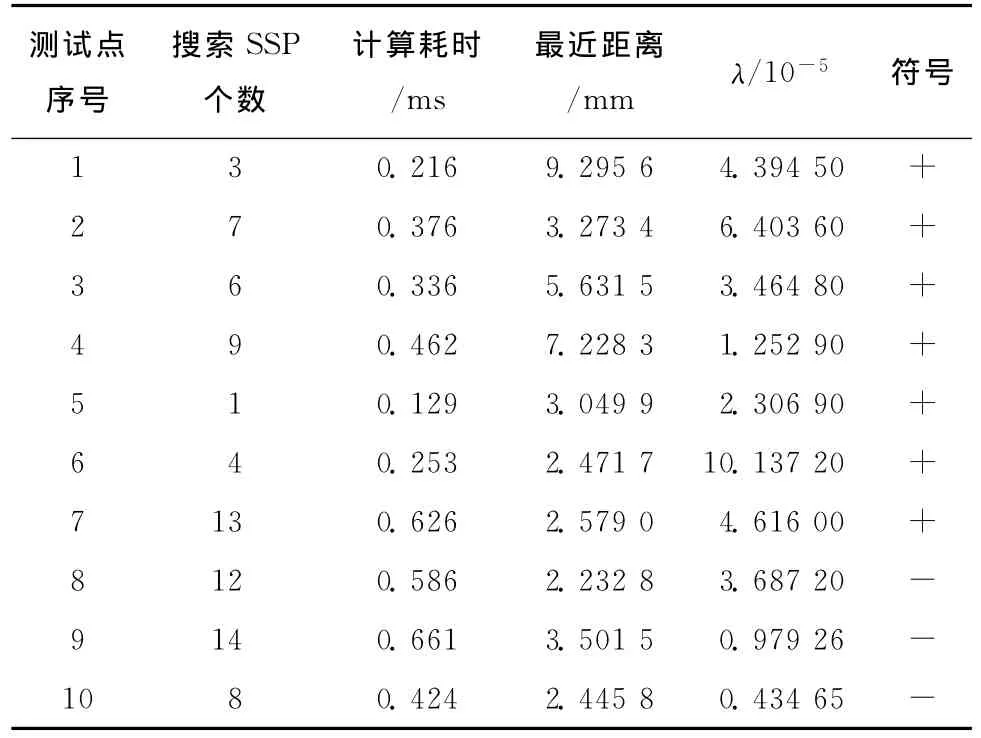
表2 计算10个测试点到Catmull－Clark细分曲面的有符号最近距离的测试结果

5 结束语

本文通过创建元胞数据结构，实现了Catmull－Clark细分曲面的分片表示。在此基础上，结合分治策略和多分辨率采样技术，提出一种计算空间点到细分曲面有符号最近距离的算法。详细描述了该算法的原理和实现步骤，并通过实例验证了算法的正确性和有效性。测试结果表明该算法稳定性强，计算效率高，计算结果准确。以本算法为基础，计算细分曲面之间的最近距离，将是未来的研究方向。

［1］XU Rufeng，CHEN Zhitong，CHEN Wuyi．Grid algorithm for calculating the shortest distance from spatial point to free－form surface［J］．Computer Integrated Manufacturing Systems，2011，17（1）：95－100（in Chinese）．［徐汝锋，陈志同，陈五一．计算点到曲面最短距离的网格法［J］．计算机集成制造系统，2011，17（1）：95－100．］

［2］XIONG Zhigang，ZHANG Guankang．The algorithm research of minimum distance between two sculptured surfaces［J］．Journal of Engineering Graphics，1990，10（2）：27－31（in Chinese）．［熊志刚，张关康．雕塑曲面间最小距离的研究［J］．工程图学学报，1990，10（2）：27－31．］

［3］SU Zhijian，WU Xutang，MAO Shimin．Genetic algorithms for solving the minimum distance between bezier curves and surfaces［J］．Machinery Design ＆ Manufacture，2003（6）：56－57（in Chinese）．［苏智剑，吴序堂，毛世民．遗传算法在求解空间曲线与曲面间最短距离中的应用［J］．机械设计与制造，2003（6）：56－57．］

［4］LIAO Ping．Using particle swarm optimization algorithm to calculate the minimum distance from point to complex surface［J］．Computer Simulation，2009，26（8）：176－178（in Chinese）．［廖 平．用粒子群优化算法计算点到复杂曲面最短距离［J］．计算机仿真，2009，26（8）：176－178．］

［5］FANG Xiang，BAO Hujun，WANG Ping'an，et al．Algorithm for fast calculating the nearest distance between space point and arbitrary polyhedron［J］．Journal of Computer Aided Design ＆ Computer Graphics，2001，13（9）：788－792（in Chinese）．［方 向，鲍虎军，王平安，等．点到任意多面体距离的快速计算方法［J］．计算机辅助设计与图形学学报，2001，13（9）：788－792．］

［6］ULLRICH T，SETTGAST V，KRISPEL U，et al．Distance calculation between a point and a subdivision surface［C］／／Proceedings of Vision，Modeling，and Visualization．Saarbrücken，Germany：MPII，2007：161－169．

［7］CATMULL E，CLARK J．Recursively generated B－spline surfaces on arbitrary topological meshes［J］．Computer－Aided Design，1978，10（6）：350－355．

［8］ZHANG J H，WANG G P．Improved error estimate for extraordinary Catmull－Clark subdivision surface patches［J］．The Visual Computer，2007，23（12）：1005－1014．

［9］CHENG F，YONG J．Subdivision depth computation for Catmull－Clark subdivision surfaces［J］．Computer Aided Design ＆Applications，2006，3（1／2／3／4）：485－494．

［10］MUSTAFA G，CHEN Falai，DENG Jiansong．Estimating error bounds for binary subdivision curves／surfaces［J］．Journal of Computational and Applied Mathematics，2006，193（2）：596－613．

［11］HUANG Zhangjin，DENG Jiansong，WANG Guoping．A bound on the approximation of a Catmull－Clark subdivision surface by its limit mesh［J］．Computer Aided Geometric Design，2008，25（7）：457－469．

［12］KRABMER P，CAZIER D，BECHMANN D．Extension of half－edges for the representation of multi－resolution subdivision surfaces［J］．The Visual Computer，2009，25（2）：149－163．

［13］DEFLORIANI L，KOBBELT L，PUPPO E．A survey on data structures for level－of－detail models［J］．Advances in Multi－resolution for Geometric Modelling，Series in Mathematics and Visualization，2004：49－74．DOI：10．1007／3－540－26808－1＿3．

［14］SETTGAST V，MÜLLER K，FÜNFZIG C，et al．Adaptive tesselation of subdivision surfaces［J］．Computers and Graphics，2004，28（1）：73－78．

［15］HALSTEAD M，KASS M，DEROSE T．Efficient fair interpolation using Catmull－Clark surfaces［C］／／Proceedings of SIGGRAPH 93．New York，N．Y．，USA：ACM，1993：35－44．