DSMC方法中的统计噪声分析
李志辉,方 明,唐少强
(1.中国空气动力研究与发展中心超高速研究所,四川 绵阳 621000;
2.北京大学工学院,北京 100871;3.国家计算流体力学实验室,北京 100191)
0 引 言
基于分子运动与碰撞随机统计模拟的直接模拟Monte Carlo(DSMC)方法[1]自1963年 G.A.Bird将其发展用于稀薄气体流动模拟以来,经过四十多年的发展,已在求解稀薄过渡领域飞行器绕流中取得巨大成功[2-9],从复杂高超声速气动力/热流动模拟到细观速度分布函数的非平衡表征均得到了实验的验证与支持。基于 对 DSMC 方 法 应 用 研 究 实 践[7,10-11]体会到,该方法因其概率统计模拟实质,其误差来自两个方面,一是计算中的网格尺寸和时间步长,二是统计抽样中的涨落。如何控制稀薄气体动力学DSMC方法统计噪声,提高计算效率与精度,一直是人们研究感兴趣的问题[12-16]。文献[13]中分析了输运系数和网格尺寸之间的关系,其结论是网格尺度不应大于气体分子平均自由程。文献[14]分析了输运系数和时间步长之间的关系,其结论是时间步长不应大于气体分子平均碰撞时间尺度。这些与实际模拟计算的经验相吻合。关于DSMC方法模拟中抽样的统计涨落,文献[12]给出了统计量收敛速度的一般规律,即收敛速度为样本容量 N 的O(N-1/2)。文献[15]中给出了傅里叶热流计算中温度的统计涨落,文献[16]从统计力学角度分析了统计量的涨落现象。在DSMC方法中,最重要的两个统计宏观量是代表动量的速度和代表能量的温度,本文尝试从数理统计角度对这两个量的统计噪声进行初步分析,给出控制和减轻DSMC模拟结果统计涨落的方法和途径。
1 DSMC方法
气体分子运动论的基本控制方程是Boltzmann方程[17]:

其考察的是微观粒子的速度分布函数f基于位置空间、速度空间在任一时刻由非平衡态向平衡态的演化[17-18,20],这 是 一 个 高 度 非 线 性 高 维 积 分 - 微 分 方程。该方程的理论解只在极其简单的情况下存在,一般问题的数值求解一直是研究的热点问题[18-23]。
DSMC方法巧妙地利用上述方程的碰撞松弛演化特征,从微观分子运动论概率统计原理出发,将分子的运动和它们之间的碰撞解耦,用有限个仿真分子代替大量的真实气体分子,仿真分子的位置坐标、速度分量以及内能被记录下来,其值因仿真分子的运动、与边界的相互作用以及仿真分子间碰撞而随时间改变,最后通过统计网格内仿真分子运动状态实现对真实气体流动的模拟[1-11]。该方法尽管不是对Boltzmann方程的离散与直接求解,但其与Boltzmann方程关于分子混沌与二体碰撞的假设是一致的,文献[24]研究结果表明,当模拟分子数趋于无穷时,DSMC方法得到的粒子分布函数收敛到Boltzmann方程的一种修正形式。DSMC方法是对Boltzmann方程或其模型方程的一种统计模拟,为了保证随机统计模拟结果的真实性,该方法要求用于分子碰撞取样的物理空间网格尺度小于气体分子平均自由程,且用于将仿真分子运动与碰撞解耦的时间间隔Δt小于平均碰撞时间。该方法得到的是模拟分子的微观信息,人们通常关心的宏观流动量可以从微观信息的统计平均得到。如宏观速度可定义为

这里的括号〈〉表示系综平均;记分子热运动速度c=v-V0。宏观温度可定义为

这里的c表示热运动速度的大小。
上述宏观量均定义为系综平均,实际的DSMC模拟过程中,如果每个网格里的仿真分子数很有限,不可避免地导致统计上的噪声波动,以致掩盖有用信息。从数学角度分析统计噪声对统计量的影响程度并提出控制统计噪声的理论规则与途径,正是本文希望探索的工作。
2 统计噪声的数学分析
在流场的DSMC方法模拟中,总是先让流场演化足够长的时间,使其充分发展,然后开始做统计抽样。为了减小统计涨落的影响,一般采用多次统计求平均值的方法。在统计的过程中,各网格中模拟分子的数目变化不大。为了数学分析的方便,假设每个网格中模拟分子的数目保持不变,对应第j个网格中模拟分子的个数为Nj。根据平衡气体统计理论[12,25],第j个网格中模拟子的速度分量ui、vi及wi应该满足正态分布体的宏观流动速度,为该网格处的气体流动温度,k为玻尔兹曼常数,m为分子质量。
2.1 噪声、统计相对涨落及置信度的定义

上面所定义的相对统计涨落ε是针对流场的每一个网格处。对于整个流场,我们定义统计量两种形式的全局相对统计涨落。第一种形式是全局最大相对统计涨落Emax

其反映的是整个流场中噪声影响的极大值。第二种形式是全局平均相对涨落Eave
这里F表示整个流场区域,V(F)为区域F的体积,其反映的是噪声对于整个流场之影响的总体平均效应。可以根据流场特征,选择适当的相对统计涨落来表示。
由于统计量存在随机性,统计量的相对统计涨落是基于概率意义下表述的。为此,我们定义统计量在相对统计涨落ε下的置信度[25]α满足

其中α为0<α<1,称1-α为置信水平,∑为在此置信水平下相对统计涨落的上界。
2.2 速度的相对统计涨落
第n次抽样时,第j个网格处某方向上(比如y方向)的宏观速度Vj,n由式(2)给定为

其中,vi是网格中第i个模拟分子在该方向上的速度。模拟共进行N次抽样,得到的第j个网格处该方向上的宏观流动速度Vj定义为

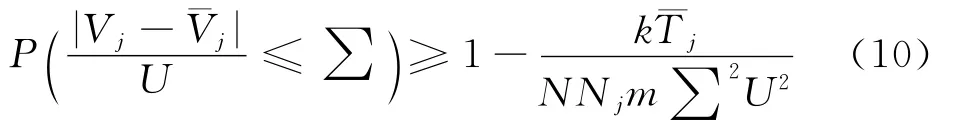
此处U为参考速度。若取参考速度U为该网格处气体流动的当地速度j,且鉴于第j个网格处的声速ac满足
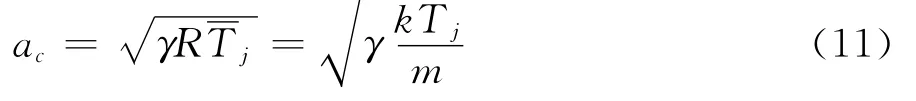
即有

其中,Ma为第j个网格处气体流动当地马赫数,γ为气体的绝热指数。
结合式(4)、(7)及(12),可得

上式表明,∑越大越好。相对统计涨落允许波动的范围越大,上限∑越大,其置信水平便越高。另一方面,从概率论角度来说,∑是在一定置信水平下相对统计涨落的上限,则越小越好。平衡二者,上式取等号。这样,在置信水平不低于1-α的条件下,网格j处速度Vj的相对统计涨落为

该公式意味着,当取参考速度U为网格j处当地气流速度¯Vj时,速度的相对统计涨落与流动马赫数成反比,与抽样次数成平方根反比例关系。
若(10)式中U取为一般参考速度,则有

即相对统计涨落与参考速度成反比,与流场温度的平方根成正比,且与抽样次数的平方根成反比。
2.3 温度的相对统计涨落
同上,第n次抽样时,第j个网格处的宏观温度Tj,n由式(3)给定为


通过N次抽样,第j个网格处的宏观温度Tj定义为雪夫不等式,同样可以得到,若取参考温度为流场温度,此时,在置信水平为1-α下,温度Tj的相对统计涨落为


即相对统计涨落除与抽样次数有关外,还与流场温度成正比、与参考温度成反比。
需要指出的是,公式(14)和(18)的结论较为简单,但其参考值为流场参数的准确值,实际计算不便操作;式(15)和(19)结论形式复杂些,但参考值的选取根据流场情况易于实现。鉴于流场中某些区域速度很小,尤其是相当低马赫数流动问题,需要控制DSMC模拟过程中速度的相对统计涨落量,可采用(15)式为模拟准则。对于速度较均匀变化的高温非平衡流场,需要考察流场温度的相对统计涨落,可采用(19)式。一般来说,相对统计涨落变化较大,实际应用时,通常考察最大相对统计涨落Emax或全局平均相对涨落Eave为宜。计算中,主要通过选择适当的参考值,控制Emax、Eave的大小,可以采用两种方式,一是增大网格内模拟分子的个数,然而这种方式又会大大增加计算内存为代价,二是增大抽样统计的次数(增大N),通过增加计算时间来实现,这种方式是降低DSMC统计涨落更适合选取的途径。
该公式意味着,温度的相对统计涨落只与统计抽样次数的平方根成反比,而与流场的宏观参数无关。
若取参考温度为Tref,则温度的相对统计涨落为
3 算例与结果分析
3.1 Couette流动计算分析
Couette流动是一种较为简单而经典的边界值问题,两个相对运动的无限大平行平板相距H、置于相同温度Tw,向相反方向沿各自平面分别以Uw速度运动。取两平板距离的中央为坐标原点,x轴为运动方向,y轴与之垂直。以具有温度Tref=273K、压力Pref=0.01atm的氩气作为模拟气体,假设Tw=Tref,变径软球(VSS)分子模型ω=0.81、α=1.4被用来描述分子间相互作用。为检验上述结论,选择式(14)、(15)作为控制DSMC方法模拟结果相对统计涨落的准则关系式,其中U取为平板速度。需要说明的是,在模拟过程中,控制每个网格中的模拟分子个数Nj是比较困难的,通常的做法是控制模拟的流场分子总数Nt,可以认为这两者是等效的。根据上述公式,我们通过设置板速Uw、模拟分子总数Nt和抽样次数N的变化来观察DSMC方法模拟得到的Couette流动速度的统计噪声变化特点。图1~图4分别绘出Kn=0.1128情况下,不同板速、不同模拟分子数与抽样次数得到的Couette流动上半槽道内无量纲流动速度沿板间距离分布比较。由式(15)知板速Uw对DSMC模拟结果相对统计涨落的影响是反比例关系,图1中的速度分布可以很好地说明这一点。图1(a)绘出固定模拟分子总数Nt=1000和抽样次数 N=20000,不同板速Uw=0.025 Ma、0.05 Ma、0.1 Ma、0.2 Ma引起的 Couette流动速度分布模拟结果,相互比较看出,在固定Nt和N 的情况下,Couette流动速度相对统计涨落即模拟精度高低与板速Uw的大小关系密切,Uw越低,DSMC结果统计涨落越大,如Uw=0.025 Ma情况,Couette流动速度的相对统计涨落甚为严重,几乎掩盖真实的气体流动速度分布;而Uw增大,同样情况下得到的DSMC结果统计涨落明显减小,如Uw=0.2 Ma对应的Couette流动速度呈现相当光滑分布,见图中虚线表示;由于不同计算条件下相对统计涨落ε形式表现为杂乱无章,为了定量刻画其变化幅度,图1(b)绘出给定上述Nt和N值条件下,不同板速引起的Couette流动速度的全局最大相对统计涨落Emax和全局平均相对统计涨落Eave,该图是对数图像,其中虚线由不同情况下Emax拟合得到、点线由Eave拟合得到,结果表明Emax和Eave均在斜率为-1的拟合直线附近散布。该图还说明,Emax与Eave之间差一个常数量,控制Emax相对于控制Eave更为困难。如若把相对统计涨落控制在1%以下,在Nt=1000和N=20000的条件下,采用控制Eave的办法,对于板速大于0.1 Ma的Couette流动就能满足要求,而式(15)表明若采用控制Emax的办法,只有板速大于0.4 Ma的Couette流动才能达到要求。图2(a)绘出固定板速Uw=0.025 Ma和抽样次数N=20000,使用不同模拟分子总数Nt=1000、4000、16000、64000得到的结果,图中看出,在固定板速Uw和N 的情况下,模拟分子总数Nt越少,如Nt=1000,DSMC结果统计涨落越大,对此较低板速Uw=0.025 Ma引起的Couette流动,只有在模拟分子总数增加到一定程度Nt=64000时,DSMC模拟得到的流动速度才较为光滑可行;图2(b)给出相应的全局最大相对统计涨落Emax和全局平均相对统计涨落Eave,该图也是对数图像,结果表明Emax和
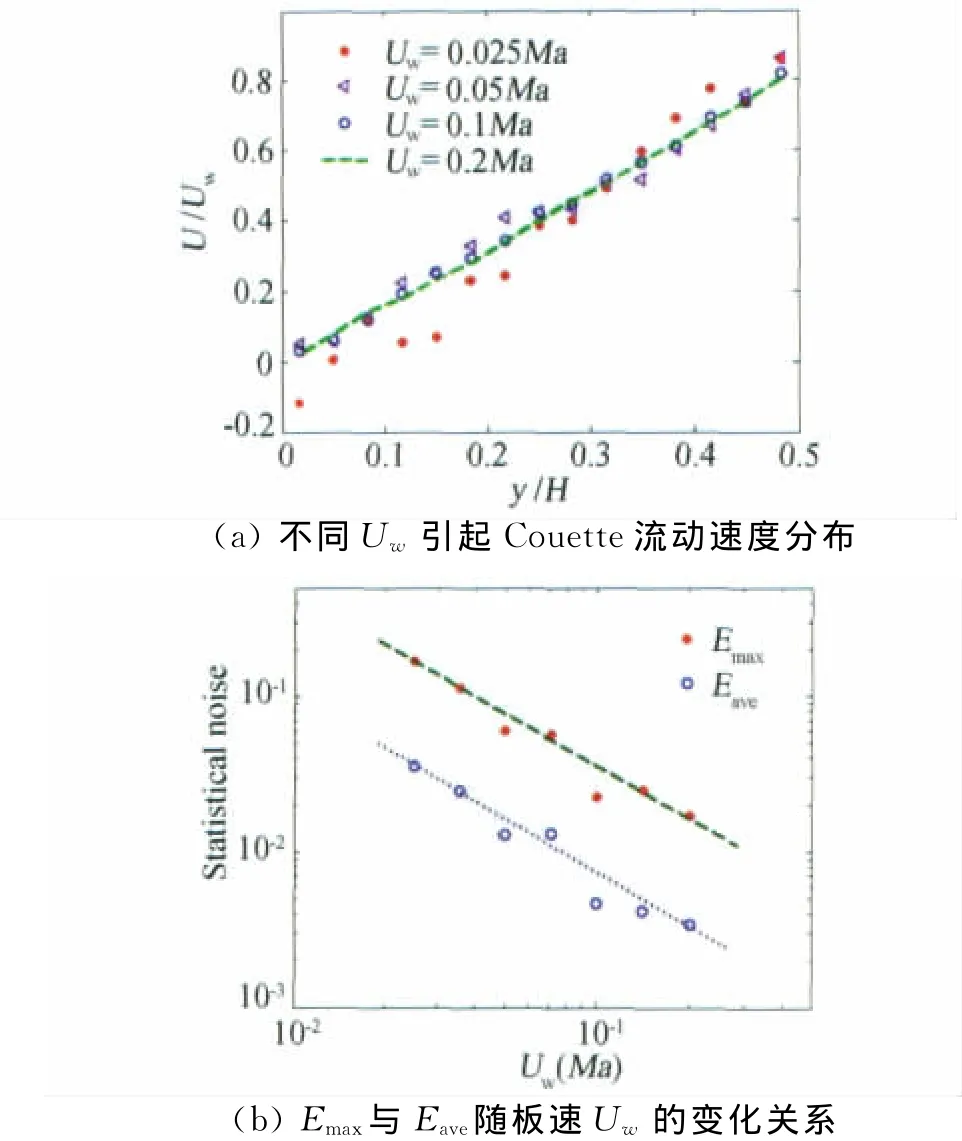
图1 不同Uw引起Couette流动速度DSMC模拟值与相对统计涨落变化关系Fig.1 Velocity distribution of Couette flow and relative statistical fluctuations under different Uwfrom DSMC simulation

图2 不同模拟分子数得到的Couette流动速度DSMC模拟值与相对统计涨落Fig.2 Velocity distribution of Couette flow and relative statistical fluctuations under different Ntfrom DSMC simulation
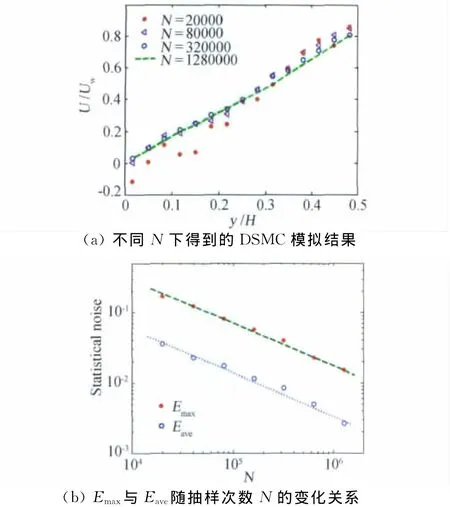
图3 不同抽样次数得到的Couette流动速度DSMC模拟值与相对统计涨落Fig.3 Velocity distribution of Couette flow and relative statistical fluctuations under different Nfrom DSMC simulation
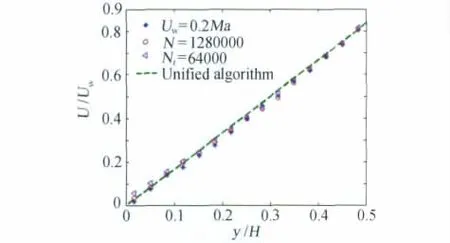
图4 不同模拟条件下得到的Couette流动速度DSMC模拟值与统一算法结果比较Fig.4 DSMC simulated velocity distribution under different conditions with the comparison of results from the unified algorithm
Eave均在斜率为-1/2的直线附近散布,两者之间也是差一个常数量。从图中可以看出,对此Uw=0.025 Ma的Couette流动模拟,若固定N=20000,则Nt增加到Nt=32000时在95%的置信水平下,Eave就可控制在1%以下;如若控制Emax在1%以下,根据公式(15),此时模拟分子总数Nt须在105以上,这需要比控制Eave多得多的计算内存,显示出本文开展DSMC方法统计噪声控制规则研究的现实意义。关于速度的相对统计涨落公式(14)、(15)也说明统计抽样次数对流动速度统计噪声的影响呈平方根反比例关系,这一点可以由图3的计算结果得到很好地说明。图3(a)、(b)分别绘出固定板速Uw=0.025 Ma和模拟分子总数Nt=1000,取不同抽样次数N=20000、80000、320000、1280000得到的 DSMC 模拟结果及其全局最大相对统计涨落Emax和全局平均相对统计涨落Eave,显示出DSMC方法对用于统计抽样的次数具有较强的依赖性,如果N太少,如图中N=20000所得到的速度分布统计涨落就相当大,只有当抽样次数达到N=1280000这样的量级,所得到的DSMC统计量就表现出较为光滑分布。图3(b)绘出Emax、Eave的对数图像分布,结果表明对此Uw=0.025 Ma的Couette流动模拟,若将全场模拟分子总数固定在Nt=1000的条件下,Emax和Eave在斜率为-1/2的拟合线附近散布,两者之间依然差一个常数量。如希望把统计涨落控制在1%以下,采用Eave则抽样次数达到640000就可满足,而若采用控制Emax的办法则需统计抽样至少6×106次以上,这将以巨大的计算时间开支为代价。为了考察图1~图3描述的三种情况下DSMC模拟值的准确性,图4绘出相应于(a)Uw=0.2 Ma(设置 N 为20000及 Nt为1000)、(b)Nt=64000(设置Uw为0.025 Ma及N 为20000)、(c)N=1280000(设置Uw为0.025 Ma及Nt为1000)三种情况得到的Couette平板间速度分布与直接求解Boltzmann模型方程的统一算法[26]结果定量化比较,看出只要按照本文提出的相对统计涨落理论规则(14)、(15)式确定模拟参数,上述三种情况所得到的DSMC模拟值就彼此吻合且与文献[26]统一算法计算分布在误差范围内相当一致。另一方面,由式(15)可计算出上述三种情况下Couette流动速度DSMC模拟值的最大相对统计涨落Emax在95%的置信水平下为大约2.3%,全局平均相对统计涨落Eave则低于1%,三种情况下得到的DSMC模拟值均趋于统一算法[26]结果。图1~图4证实本文关于DSMC模拟结果统计噪声的理论推导公式(14)、(15)的可靠实用性。鉴于一般情况下计算流场的来流速度是给定的,为了减小流场速度统计噪声的影响,应该选择控制模拟分子总数Nt和抽样次数N 的大小。根据图2、图3所反映的计算结果证实,控制这两个模拟参数的取值,对于减小统计噪声的效果是一样的。在实际计算中,为了减小计算机内存负荷,一般可采取如图3所示通过增大抽样次数N,延长DSMC模拟计算时间,来获得较小统计噪声的DSMC模拟结果。通过上述过渡流区Couette剪切流动算例的计算比较与分析也看出,来流速度大小对DSMC统计噪声的影响很大;来流速度越小,获得小噪声的流场速度分布越困难,可根据式(15)所反映的计算规则来选取DSMC模拟参数,并将统计噪声控制在所希望的计算精度范围内。
3.2 激波内流动计算研究
正激波内流动作为从均匀超声速上游(状态1)到均匀亚声速下游(状态2)流动的过渡,由于其一维属性以及不考虑气面边界相互作用,常用作一种检验数值方法与计算规则的偏离热力学平衡态流动算例。拟定来自文献[20,27]相同的计算条件,使用变软球(VSS)分子模型,对马赫数Ms=1.55的激波内流动问题进行DSMC模拟研究。为了检验2.3节推导出的流场温度相对统计涨落表达式,使用式(18)作为控制DSMC方法模拟结果相对统计涨落计算规则。在处理温度的DSMC模拟统计噪声时,若取参考温度Tref为流场温度¯Tj,流场宏观流动参数对温度的相对统计涨落影响不明显。根据3.1节模拟体会,由于模拟分子总数Nt和抽样次数N 对DSMC模拟结果相对统计涨落的影响效果一样,此处考虑相同的计算流场模拟分子总数Nt=20841(计算过程中总的模拟分子数存在一定波动),选取不同的统计抽样次数N=500、1000、2000、4000、8000、16000、32000和64000,考察统计噪声对DSMC模拟结果的影响。图5绘出三种不同抽样次数N=500、2000和8000得到的温度分布,看出对于这种较低马赫数激波内流动模拟,统计抽样次数对DSMC模拟结果噪声影响很大;对于选取太少的N=500,所得到的温度分布统计涨落表现得很严重;当N值增大,激波轮廓的统计波动明显减小;若采用较大的统计抽样次数如N=8000时,所得到的温度分布轮廓线较光滑,见图中虚线表示。图6给出了分别在三种更高抽样次数N=8000、16000和32000下得到的温度分布与来自文献[20,27]的统一算法结果比较,图中显示出当抽样次数大于8000时统计噪声对模拟结果的影响已经不大。综合图5和图6不同抽样次数下激波结构内流动温度分布DSMC模拟结果变化特点,可看出N值由小到大得到的DSMC模拟值均收敛并完全吻合于直接求解Boltzmann模型方程的统一算法结果,反映出统计量的相对统计涨落随着抽样次数增大而减弱,当统计抽样次数增大到一定程度,DSMC模拟将收敛于共同的真值。为了将DSMC模拟值与实验数据比较,图7绘出相应于N=32000模拟得到的密度分布与统一算法结果[20,27]及实验数据[28]相比较,可看出三种结果变化趋势相当一致。图8绘出不同抽样次数下DSMC模拟得到的激波内流动温度分布的全局最大相对统计涨落Emax与全局平均相对统计涨落Eave随抽样次数N的变化关系对数图像,可看出Emax、Eave分别散布在两条平行直线附近,该直线分别由不同情况下Emax、Eave值拟合而来,其斜率均为-1/2,这直接证实关于温度分布DSMC模拟结果相对统计涨落的表达式(18)的正确性,该式给出了DSMC模拟热力学非平衡温度场问题所需要统计抽样次数的选取准则。统计涨落给出一个波动范围,最终真实计算的涨落值都落在这个范围之内。图中数据分析表明,在抽样次数N上升到104量级时,最大相对统计涨落可以控制在1%以内,而此时平均相对统计涨落已降至千分之一以内。该图还反映了全局最大相对统计涨落Emax和全局平均相对统计涨落Eave具有完全相似的变化关系,Eave较之于Emax更为苛刻,一般计算只要将Eave控制在所要求计算精度就可以了,在实际应用中可根据客观情况选择判断。
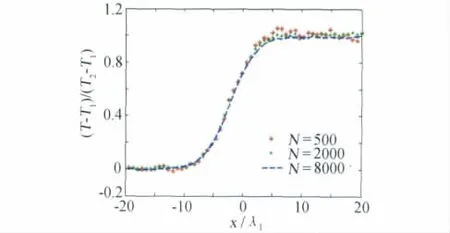
图5 不同抽样次数N=500、2000、8000得到的Ms=1.55激波内流动温度分布Fig.5 Temperature distribution for Ms=1.55shock wave under different N=500,2000,8000
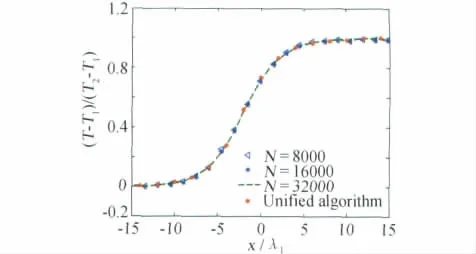
图6 N=8000、16000、32000得到的激波结构温度分布DSMC模拟值与统一算法结果比较Fig.6 DSMC simulated temperature distribution for Ms=1.55under different N=8000,16000,32000 with the comparison of results from the unified algorithm
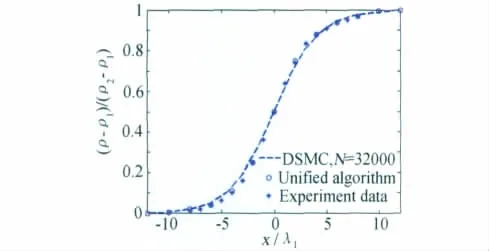
图7 N=32000得到的激波结构密度分布DSMC模拟值与统一算法、实验数据比较Fig.7 DSMC simulated density distribution under N=32000with comparison of the results from the unified algorithm and the experiment data

图8 DSMC模拟激波内流动温度分布的Emax、Eave随统计抽样次数N变化关系Fig.8 Relative statistical fluctuations Emaxand Eaveof temperature distribution under different Nfrom DSMC simulation
4 结束语
本文在定义DSMC模拟结果相对统计涨落的基础上,引入概率统计置信度概念,通过数学分析推导出流场速度与温度的相对统计涨落表达式。在此基础上,以过渡流区Couette剪切流和激波内流动为研究对象,进行DSMC模拟研究,分别计算分析了Couette流动中速度的相对统计涨落、激波结构内流场温度的相对统计涨落及其变化规律与影响因素,证实本文关于DSMC方法中统计噪声的理论推导与控制规则的正确性。研究表明,在一定的置信度下,DSMC模拟结果的相对统计涨落除与网格内模拟分子数及统计抽样次数的平方根成反比例,流场速度的相对统计涨落还与流场马赫数成反比,而温度的相对统计涨落与流场宏观参数无关。得到了有关速度与温度相对统计涨落更具一般性的结论,为DSMC方法模拟中控制并降低统计量的相对统计涨落提供了理论依据。而且计算体会到,为了控制流场参数的相对统计涨落,需要增大网格内模拟分子数或增大DSMC模拟过程中统计抽样的次数,且二者是等效的,可根据实际计算需要,进行选取。一般为了控制计算内存,通常以增大DSMC统计抽样次数,增加计算时间来降低统计量的相对统计涨落。
[1] BIRD G A.Approach to translational equilibrium in a rigid sphere gas[J].Phys.Fluids,1963,6(10):1518-1519.
[2] BORGNAKKE C,LARSEN P S.Statistical collision model for Monte Carlo simulation of polyatomic gas mixture[J].J.of Comput.Phys.,1975,18(4):405-420.
[3] PHAM-Van DIEP G,ERWIN D,MUNTZ E P.Nonequilibrium molecular motion in a hypersonic shock wave[J].Science,1989,245(4918):624-626.
[4] CARLSON A B,HASSAN H A.Direct simulation of reentry flows with ionization[R].AIAA Paper 90-144,1990.
[5] BIRD G A.Molecular gas dynamics and the direct simulation of gas flows[M].Clarendon Press,Oxford,1994.
[6] 樊菁,沈青.过渡领域高超声速圆柱绕流的直接模拟[J].空气动力学学报,1995,13(4):405-413.
[7] 李志辉,吴振宇.阿波罗指令舱稀薄气体动力学特征的蒙特卡罗数值模拟[J].空气动力学学报,1996,14(2):230-233.
[8] 吴其芬,陈伟芳.高温稀薄气体热化学非平衡流动的DSMC方法[M].长沙:国防科技大学出版社,1999.
[9] IVANOV MS,VASHCHENKOV P,KASHKOVSKY A,Numerical investigation of the EXPERT reentry vehicle aerothermodynamics along the descent trajectory[R].AIAA 2007-4145,2007.
[10]LI Z H,XIE Y R.Technique of molecular indexing applied to the direct simulation Monte Carlo method[A].Proc.of 20th International Symposium on Rarefied Gas Dynamics[C].ed.by Shen C,Peking Univ.Press,pp205-209,1997.
[11]LIANG J,LI Z H,LI Z H.DSMC computation of rarefied flow around a three-dimensional re-entry capsule[A].3th Sino-Russian Hypersonic Flow Conference[C].SRHFC-3,Wulumuqi,China,Sep.,2002.
[12]裴鹿成,张孝泽.蒙特卡罗方法及其在粒子输运问题中的应用[M].北京:科学出版社,1980.
[13]FRANCIS J.ALEXANDER.Cell size dependence of transport coefficients in stochastic particle algorithms[J].Phys.Fluids,1998,10(6):1540-1542.
[14]ALEJANDRO L.GARCIA.Time step truncation error in direct simulation Monte Carlo[J].Phys.Fluids,2000,12(10):2621-2633.
[15]RADER D J,GALLIS M A,TORCZYNSKI J R.Direct simulation Monte Carlo convergence behavior of the hard-sphere-gas thermal conductivity for Fourier heat flow[J].Phys.Fluids,2000,18(7):1-16.
[16]NICOLAS G.HADJICONSTANTINOU,ALEJANDRO L.GARCIA,MARTIN Z.BAZANT,GANG HE.Statistical error in particle simulations of hydrodynamic phenomena[J].J.of Comput.Phys.,2003,187(1):274-297.
[17]CHAPMAN S,COWLING T G.The mathematical theory of non-uniform gases[M].3rd ed.,Cambridge Univ.Press,1990.
[18]YEN S M.Numerical solution of the nonlinear Boltzmann equation for nonequilibrium gas flow problems[J].Ann.Rev.Fluid.Mech,1984,16(1):67-97.
[19]YANG J Y,HUANG J C.Rarefied flow computations using nonlinear model boltzmann equations[J].J.of Comput.Phys.,1995,120(2):323-339.
[20]LI Z H,ZHANG H X.Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J].J.of Comput.Phys.,2004,193(2):708-738.
[21]ALEXEI H,PIOTR K.Fast numerical method for the Boltzmann equation on non-uniform grids[J].J.of Comput.Phys.,2008,227(13):6681-6695.
[22]LI Z H.Gas-kinetic unified algorithm for re-entering complex problems covering various flow regimes by solving Boltzmann model equation[M].Advances in Spacecraft Technologies,Jason Hall(Ed.),InTech Publisher,Chapter 14,2011:273-332.
[23]MORRIS A B,VARGHESE P L,GOLDSTEIN D B.Monte Carlo solution of the Boltzmann equation via a discrete velocity model[J].J.of Comput.Phys.,2011,230(4):1265-1280.
[24]WAGNER W.A convergence proof for Bird's direct simulation Monte Carlo method for the Boltzmann equation[J].J.Sat.Phys.,1992,66(3/4):1011-1044.
[25]汪仁官.概率论引论[M].北京大学出版社,1994.
[26]李志辉.稀薄流到连续气体流动问题统一算法应用研究[D].[博士后研究报告].北京:清华大学,2003.
[27]李志辉,张涵信.激波结构内流动问题的气体运动论描述[J].空气动力学学报,2007,25(4):411-418.
[28]ALSMEYER H.Density profiles in argon and nitrogen shock waves measured by the absorption of an electron beam[J].J.Fluid.Mech.,1976,74(3):497-513.

