关于傅里叶变换性质教学方法的探讨
丹 梅,曹聚亮,吴 京, 赵 锋
(国防科技大学1.电子科学与工程学院;2.机电工程与自动化学院,湖南长沙 410073)
0 引言
“信号与系统”课程的三大变换(傅里叶变换、拉普拉斯变换和z变换)中,傅里叶变换无疑是最为重要的一种变换,而傅里叶变换的性质又是其中的重点。把傅里叶变换的性质讲深讲透,有利于学生深入理解傅里叶变换,理解频域分析的思想,对其他几种变换的学习都会有所帮助。
连续时间信号傅里叶变换的性质很多,一般要求学生掌握的有:对称性、线性、奇偶性、展缩特性、时移特性、频移特性、时域微分和积分特性、频域微分和积分特性、时域卷积特性以及频域卷积特性等[1-6]。当然,不同教材的内容有些许差异,例如有的教材将相关定理和帕斯瓦尔定理列入傅里叶变换的性质内容;有些教材对于频域的微分和积分特性不讲或略讲。性质的名称也不尽相同,如对称性又称为对偶性或互易对称性,展缩特性又称为尺度变换特性,奇偶性还称为共轭对称性等,但所有教材的基本内容还是比较一致的。
如何将名目繁多的性质条理清晰地呈现给学生,需要考虑两个关键问题:①厘清各个性质间的关系和讲授顺序,先讲哪个性质,后讲哪个性质,把握好各个性质之间的联系和区别;②合理安排每个性质具体讲解内容。每个性质包含三方面内容:性质本身的数学表示、证明和应用。应用又包含两方面:一是在傅里叶变换和反变换等计算中的应用;二是该性质所表达的物理含义。后者尤其重要,挖掘各个性质蕴含的物理意义,可以增进学生的理解[7]。
1 各个性质之间的关系
傅里叶变换的性质虽然名目很多,但其实质是研究两个域(时域和频域)之间的对应关系。这种对应关系可以总结为两点:①一个域中的某些特性在另外一个域中对应什么特性?②一个域中的某种运算在另外一个域中发生什么变化?
例如,奇偶性研究的是一个域中的奇对称或偶对称在另外一个域的体现。其他性质,除了对称性之外,都是研究一个域中的某种运算(线性运算、尺度变换、平移、微分、积分和卷积)在另外一个域对应的变化。而对称性,可看做是对所有性质的一个总结,它可用照片和底片的关系来比喻。如果底片中的某种变化A,照片中以A'的形式表现出来,那么,照片中的变化A,也必然对应底片中的某种变化A″。傅里叶变换的各个性质之间的关系示于图1。
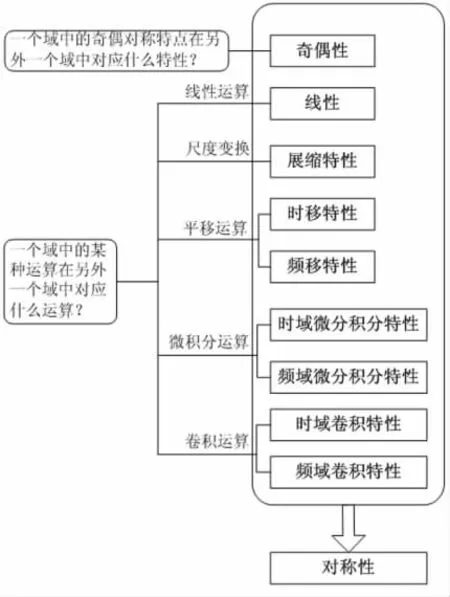
图1 傅里叶变换性质之间的关系
2 课程讲授顺序
笔者根据多年的教学实践,认为按照图2所示的顺序讲授效果会比较好。
首先是线性性质,当然该性质也可在讲解傅里叶变换定义式时给出,但由于线性性质不仅是傅里叶变换,也是后面要学习的拉普拉斯变换和z变换也具备的基本性质。笔者认为还是有必要将其作为一条性质单独列出,以示强调。在学习后面两种变换时,则可不再单独列出。对称性有其特殊重要的地位,是诸多性质中的核心,反映了傅里叶变换的实质。笔者认为,它的讲授顺序应当靠后,因为该性质本身的数学表示式不易理解,其证明也需要一定的数学技巧,放在开篇的位置讲解,学生不易接受。
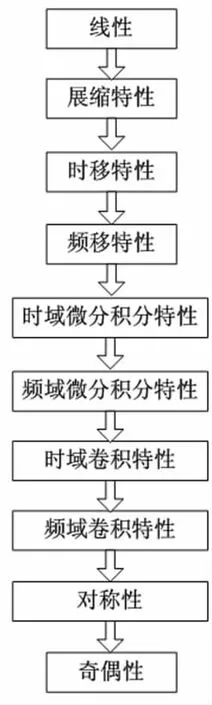
图2 傅里叶变换性质的一种讲授顺序
在给出线性性质之后,可以将展缩特性作为傅里叶变换性质的切入点,因为展缩特性不仅证明较简单,而且物理含义特别清晰直观,可以举出生活中实例作对照。磁带放音即是一例。录音机电量不足时,磁头转速慢,相当于慢速放音,即时域扩展,而声音听起来音调低沉,即对应频域压缩,高频分量减少,低频分量增多;反之,以比正常情况快的速度放音,即时域压缩,而声音听起来音调尖利,即对应频域扩展,高频分量增多。另外,还可以以通信系统中通信速度和占用频带宽度的矛盾为例,说明傅里叶变换的展缩特性。
然后才是时移、频移、时域微分积分、频域微分积分、时域卷积和频域卷积,这6条性质又可以归纳为4对,即:平移、微分、积分和卷积,可以很明显地构成时域和频域的对应,通过这4对性质的学习,已经将时域与频域的对称特点展现在学生面前,此时再讲解对称性,就是水到渠成了,因其含义已经相当明确,抽象的数学表示和推导过程已经不会构成理解上的障碍,甚至可以绕过证明过程,结合前面4对性质,直接给出对称性的数学表示和直观的解释。
最后给出奇偶性。因为奇偶性的证明过程虽然较简单,但只能停留在数学推导的层面上,不易给出生动实例。放在最后,直接给出该性质,简单说明其数学特性,详细证明过程可以留给学生课下自学。
3 对称性的应用
前面指出对称性可以看做是对所有性质的一个总结。实际上,傅里叶变换的定义式本身即体现了该性质。同时也可以直接利用傅里叶正反变换的定义式来证明该性质[8]。反之,该性质可以用于傅里叶正、反变换的求解,另外利用对称性,还可以实现时移特性与频移特性、时域微分特性与频域微分特性、时域卷积特性与频域卷积特性的互推。下面给出其推导过程。为了叙述方便,设f(t)F(ω),f1(t)F1(ω)和 f2(t)F2(ω)的推导中,都利用到展缩特性的特例:。
(1)由时移特性推导频移特性
由时移特性得:F(t-t0)2πf(-ω)e-jωt0
再利用对称性得:2πf(-t)e-jtt02πF(-ω - t0)
利用展缩特性 t→-t,ω→-ω 得:f(t)ejtt0F(ω -t0),频移特性得证。
(2)由时域微分特性推导频域微分特性
(3)由时域卷积特性推导频域卷积特性
由对称性得:
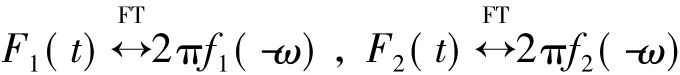
由时域卷积特性得:
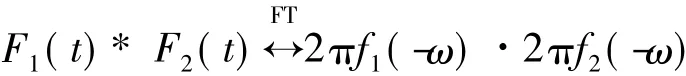
再利用对称性得:

用展缩特性,t→-t,ω→-ω,得:
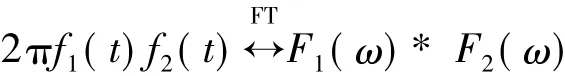
由此频域卷积特性得证。
4 结语
傅里叶变换这一部分的教学要求,是从数学概念、物理概念及工程概念上深刻理解信号频谱的含义,熟练掌握信号的频域分析方法,熟练掌握连续时间信号傅里叶变换的基本性质及应用,建立信号时域与频域的对应关系。
在这一部分的教学中,我们应该注意数学与物理意义的结合,挖掘傅里叶变换性质在实际中的应用实例。通过生活中的生动实例,激发学生学习兴趣,通过科技领域中的实例,激发学生的钻研精神。
[1] Alan V.Oppenheim著.刘树棠译.信号与系统(第二版)[M].西安:西安交通大学出版社,1998.3
[2] 郑君里等.信号与系统(第二版)[M].北京:高等教育出版社.2000,5
[3] 吴大正等.信号与线性系统分析(第四版)[M].北京:高等教育出版社
[4] [美]B.P.Lathi著.刘树棠等译.线性系统与信号(第2版)[M].西安:西安交通大学出版社,2006.4
[5] 吴京等.信号与系统分析(第二版)[M].长沙:国防科技大学出版社,2004.8
[6] 丹梅等.“信号与系统”课程教材内容比较及分析探讨[J].南京:电气电子教学学报电子信息专辑.2009.31(12):4~7
[7] 刘芸等.引导学生理解信号频谱的概念和意义[J].武汉:理工高教研究.2007.26(5):119~121
[8] 郑君里,教与写的记忆--信号与系统评注[M].北京:高等教育出版社.2005,8

