分数阶Lorenz系统的分析及电路实现*
贾红艳 陈增强 薛薇
1)(天津科技大学自动化系,天津 300222)
2)(南开大学自动化系,天津 300071)
(2013年3月12日收到;2013年3月11日收到修改稿)
1 引言
尽管分数阶的微积分理论很可能在300多年前就已经出现了,但在1960年以前,关于分数阶系统的研究很少能引起研究者的关注[1,2].这或许是由于存在着许多不一致的微积分定义,或许是由于缺乏对分数阶微积分的充分的几何解释[3].直到近几十年,尤其当发现一些实际的物理系统展现出分数阶动态特性以后,例如,管道的边界层效应、电解电极、黏弹性受阻结构等过程中都存在分数阶动态特性[4-7].关于分数阶系统的研究开始引起了越来越多的关注,随后对分数阶系统中的混沌动态研究逐渐成为了一个研究热点,相继有一些分数阶混沌系统被提出和研究,例如,分数阶的Chua’s电路[1]、分数阶的Lorenz系统[3]、分数阶的Chen系统[8-10]、分数阶的Lu¨系统[11]、分数阶的神经网络[12]、分数阶的Duffi ng振子[13]等.
通常认为在维数低于3的系统中,不能发现混沌动态,而在分数阶系统中存在混沌动态使得在维数低于3的系统中发现混沌现象成为可能.在更低维的系统中发现混沌现象或许会成为一个研究动力,促使研究者们更进一步地分析和研究分数阶混沌系统.这里所说的系统维数是指系统中所有的微分方程的阶次的总和.此外,出于应用的需要,关于分数阶混沌同步和控制研究以及电路设计等也正逐渐成为了一个研究热点[14-20].分数阶混沌理论的研究工作将为混沌应用提供一些新的技术手段,从而促进混沌应用的发展.
然而由于对分数阶混沌的研究刚刚起步,上述关于分数阶混沌系统的研究绝大多数都是通过Lyapunov指数、吸引子相轨迹图、电路仿真等数值仿真分析方法说明系统的混沌动态.而分数阶混沌系统的分岔分析以及硬件实现等却很少涉及.本文将主要通过分岔分析和模拟电路实现对分数阶Lorenz系统的混沌特性进行研究.前者可以给出分数阶系统随参数变化的演化过程,分析系统的一些动态特性,找到系统中的混沌吸引子和周期吸引子.后者不仅可以帮助从物理意义上说明混沌的存在性,而且可以为分数阶混沌应用提供电路模型.
2003年,Grigorenko和Grigorenko[3]分析了分数阶Lorenz系统的混沌动态,不仅给出了当系统维数大于或等于2.91时的一些吸引子相轨迹图和分析,而且也给出了当维数小于或等于2.91时,该系统不存在混沌动态的结论.但非常遗憾的是,2003年在和Grigorenko的私人通信中,Li证实了文献[3]中的结论是错误的,并于2004年在文献[2]中做了说明.2009年Yu等[21]进一步研究了分数阶Lorenz系统且给出了其平衡点的稳定性分析,说明了该系统的Hopf分岔现象,同时也给出了2.96维的混沌吸引子的数值仿真图.那么在更低维的分数阶Lorenz系统是否存在混沌动态呢?
本文在上述研究的基础上,首先对分数阶Lorenz系统进行了研究,发现在更低维的分数阶Lorenz系统存在着混沌现象.然后,为进一步说明混沌特性随参数变化的演化行为,又给出了不同分数阶次的系统的Lyapunov指数图、分岔图和吸引子相轨迹图,通过数值分析方法说明了分数阶Lorenz系统的混沌特性,即数值仿真结果和分岔图是一致的.最后,基于整数阶混沌电路的设计方法[22-31],用模拟电路实现了该分数阶Lorenz系统,通过模拟示波器观察到了与数值仿真一致的结果.不仅从物理意义上说明了分数阶Lorenz系统的混沌特性,也为混沌应用提供了技术上的准备.
2 分数阶Lorenz系统及其分形分析
2.1 分数阶Lorenz系统
最近,Grigorenko和Grigorenko分析了分数阶Lorenz系统的混沌动态,该系统可以被描述为
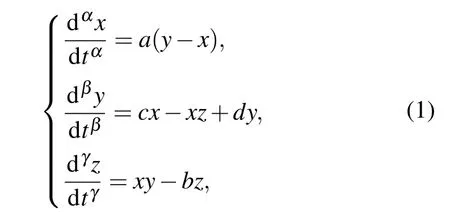
其中,a,b,c,d是系统参数,α,β,γ是分数阶次.在文献[2,3,21]中分别对该系统进行了数值仿真分析和平衡点的稳定性分析等研究,分别说明了该分数阶系统在2.91维和2.96维的混沌特性.现选取a=40,b=3,c=10,d=25,α=β=γ=0.9时,通过数值仿真可以观察到该分数阶系统在2.7维的一个混沌吸引子的相轨迹,如图1所示.
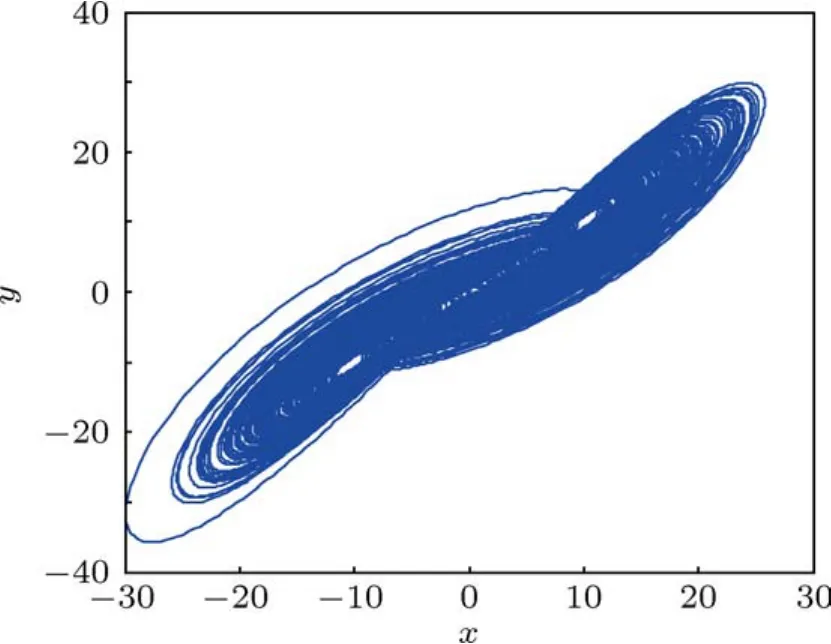
图1 分数阶Lorenz系统的混沌吸引子(α=β=γ=0.9)
2.2 分数阶Lorenz系统分形分析和数值仿真
然而,仅仅凭借图1不能说明分数阶Lorenz系统的混沌动态.为进一步对其混沌特性加以验证,下面将通过Lyapunov指数图和分岔图对其进行进一步研究.本文中采用的分数阶微分为Riemann-Liouville定义:

那么,在该定义下的Laplace变换为

这样,传递函数1/sα可以用一个近似的整数阶传递函数表示.实际上当研究分数阶系统的混沌动态时,频域传递函数近似方法是常用的数值方法之一,这种方法在很多研究中常被采用[1,2,32,33].且误差不会超过2 dB.本文分别采用了文献[1,33]中所给出的两种不同的频域近似,对分数阶Lorenz系统进行了研究,通过对Lyapunov指数图、分岔图和数值仿真分析,都发现了分数阶Lorenz系统的混沌动态.鉴于篇幅原因,本文只给出了采用文献[33]的频域近似方法的分析结果.其中所用到的近似函数分别为

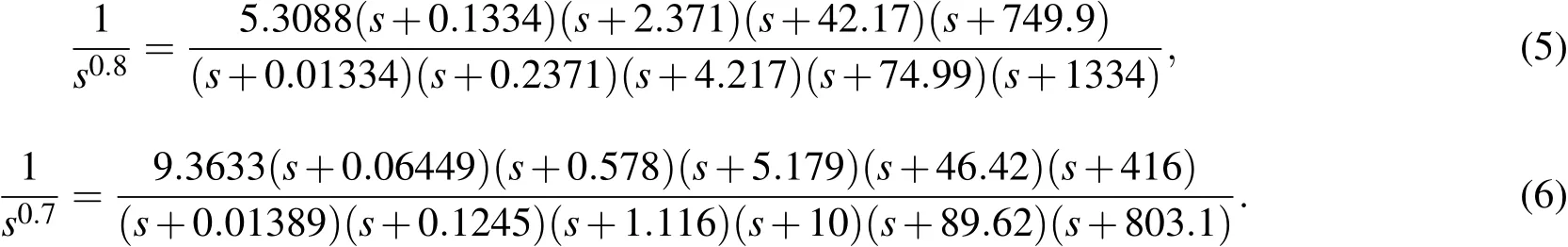
同时,基于连续整数阶混沌系统Lyapunov指数的Jacobian计算方法,本文计算了分数阶Lorenz系统的Lyapunov指数.与整数阶系统计算方法不同的是,在计算不同分数阶次Lorenz系统的Lyapunov指数时,本文将整数阶的积分器1/s转换为分数阶的积分器1/sα,就可以得到系统的相应的分数阶次的Lyapunov指数.
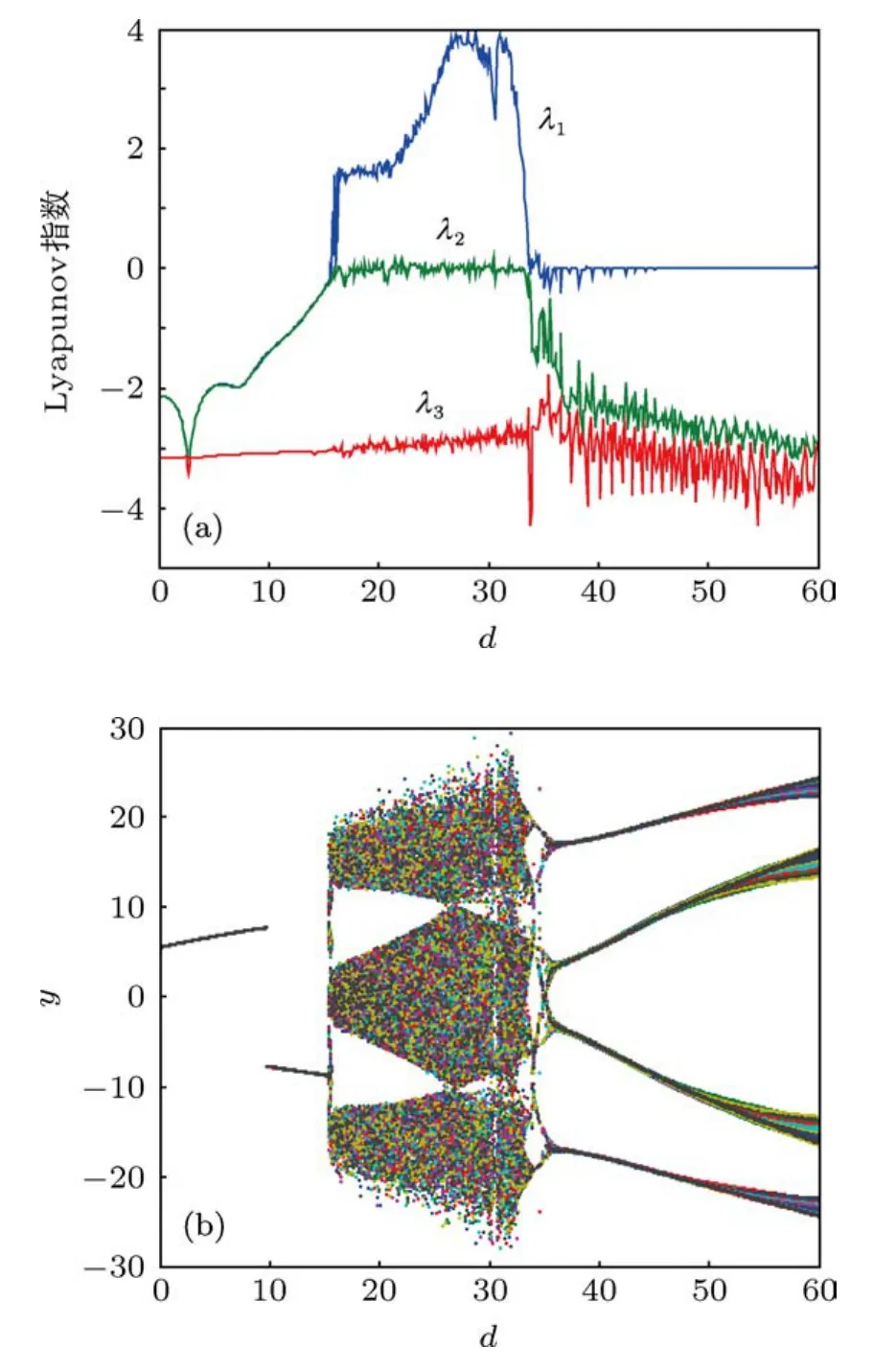
图2 分数阶次为α=β=γ=0.9的Lorenz系统的Lyapunov指数图和分岔图 (a)Lyapunov指数图;(b)分岔图
这样当a=40,c=10,b=3,变化参数d时,可以得到分数阶次为α=β=γ=0.9,系统维数为2.7的Lorenz系统的Lyapunov指数图和分岔图,如图2所示.通过对该Lyapunov指数图和分岔图分析,可以发现在2.7维的Lorenz系统的确存在混沌特性.采用相同的方法,也可以分别得到分数阶次为0.8和0.7,系统维数为2.4和2.1的Lorenz系统的Lyapunov指数图和分岔图,如图3和图4所示.
通过对上述Lyapunov指数图和分岔图的分析,可以发现当分数阶次从0.7到0.9以步长0.1变化时,即系统维数从2.1到2.7以步长0.3变化时,分数阶Lorenz系统不仅存在混沌特性,而且也存在周期特性.为了进一步验证我们的分析,本文中也给出了一些不同分数阶次或系统维数的数值仿真图.现选取a=40,b=3,c=10,当分数阶Lorenz系统的分数阶次从0.7到0.9变化时,其x-y平面的相轨迹图分别如图5所示.其中当分数阶次为0.9,a=40,b=3,c=10,分别取d=40,d=33.8时,分数阶Lorenz系统为单周期吸引子和双周期吸引子,如图5(a)和5(b)所示;当分数阶次为0.8,a=40,b=3,c=10,分别取d=40和d=41.7时,分数阶Lorenz系统为混沌吸引子和周期吸引子,如图5(c)和(d)所示;当分数阶次为0.7,a=40,b=3,c=10,分别取d=40和d=46时,分数阶Lorenz系统为渐进稳定的相轨迹和混沌吸引子,如图5(e)和(f)所示.考虑到篇幅原因,本文仅给出部分吸引子的相轨迹图.通过数值仿真观察到的吸引子相轨迹与指数图和分岔图所呈现的动态特性是一致的.

图3 分数阶次为α=β=γ=0.8的Lorenz系统的Lyapunov指数图和分岔图 (a)Lyapunov指数图;(b)分岔图
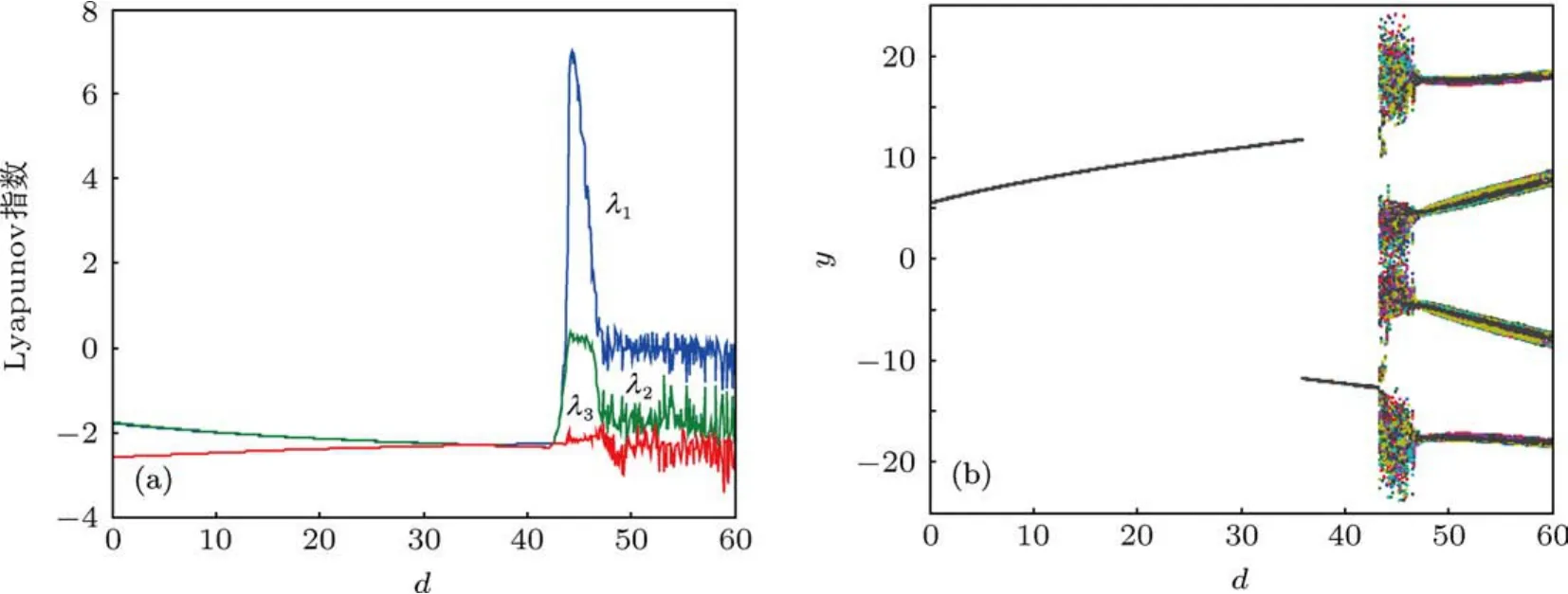
图4 分数阶次为α=β=γ=0.7的Lorenz系统的Lyapunov指数图和分岔图 (a)Lyapunov指数图;(b)分岔图

图5 分数阶Lorenz系统的x-y平面的吸引子相轨迹 (a)α=β=γ=0.9,d=40时单周期吸引子;(b)α=β=γ=0.9,d=33.8时双周期吸引子;(c)α=β=γ=0.8,d=40时混沌吸引子;(d)α=β=γ=0.8,d=41.7时周期吸引子;(e)α=β=γ=0.7,d=40时渐进稳定的相轨迹;(f)α=β=γ=0.7,d=46时混沌吸引子
3 分数阶Lorenz系统的电路实现
为了进一步从物理意义上验证分数阶Lorenz系统的混沌特性,基于整数阶混沌电路的设计方法和频域近似方法,使用电阻、电容、模拟运算放大器LF347N和乘法器AD633,本文也设计了一个模拟电路实现了0.9阶次的分数阶Lorenz系统,如图6所示.其中R5=R15=R24=1.55 MΩ,R6=R16=R25=62 MΩ,R7=R17=R26=2.5 kΩ;C1=C4=C7=0.73µF,C2=C5=C8=0.52µF,C3=C6=C9=1.1µF,上述电阻和电容的数值都是根据0.9阶次的频域近似确定的.R1=R2=2.5 kΩ,R3=R8=R9=R10=R13=R18=R19=R22=R27=R28=10 kΩ,R4=R12=R14=R21=R23=1 kΩ,R20=33.3 kΩ,R11是可调电阻,这些电阻阻值都是根据分数阶Lorenz系统的系统参数确定的,其中R11随着系统(1)中的参数d的变化而变化.这样当调节可调电阻R11时,可以通过示波器观测到混沌吸引子或周期吸引子的相轨迹,本文分别给出了x-y和y-z平面的混沌吸引子、双周期吸引子和单周期吸引子的相轨迹图,如图7所示.通过与数值仿真的结果比较,可以发现分数阶Lorenz系统的数值仿真、分形分析、电路实现的结果是一致的.
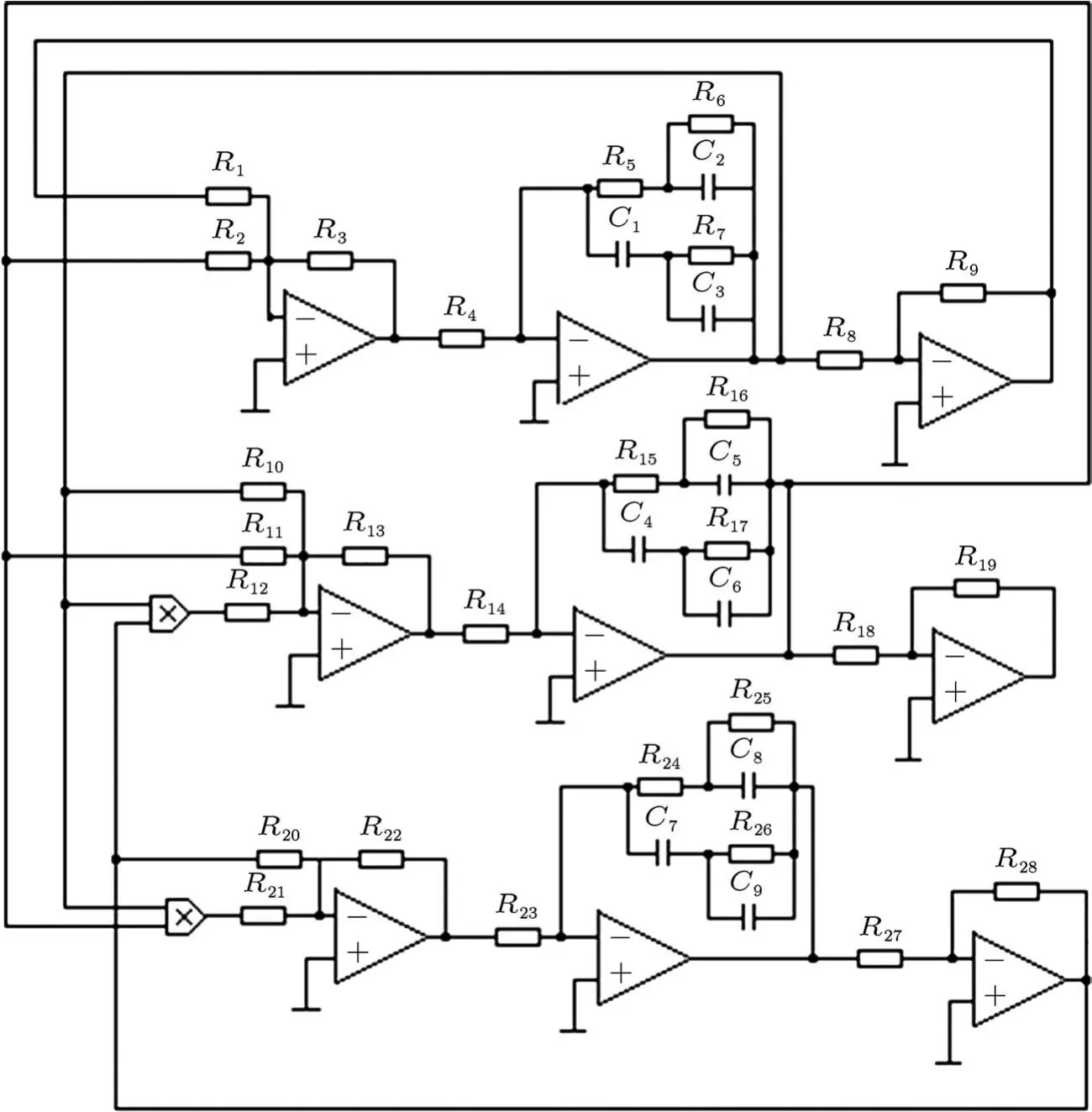
图6 分数阶Lorenz系统的模拟电路
4 结论
采用频域传递函数近似方法,研究了分数阶Lorenz系统,分别从系统的Lyapunov指数图、分岔图和吸引子相轨迹图等数值仿真分析验证了其混沌特性.与已有的研究不同的是,本文发现了该分数阶Lorenz系统丰富的动态特性,当分数阶次从0.7到0.9以步长0.1变化时,即系统维数从2.1到2.7以步长0.3变化时,分数阶Lorenz系统不仅都存在混沌特性,而且也都存在周期特性.另外,也设计了一个模拟电路实现了分数阶次为0.9的Lorenz系统,且通过示波器观测到的相轨迹图同数值仿真分析是一致的,从物理意义上进一步验证了分数阶Lorenz系统的混沌特性.上述研究结果表明,在更低维的Lorenz系统中也存在着混沌特性.本文的研究工作或许将为混沌应用提供更为丰富的分数阶模型,为其应用提供技术上的准备.

图7 示波器观测到的分数阶Lorenz系统的相轨迹 (a)x-y平面混沌吸引子;(b)y-z平面混沌吸引子;(c)x-y平面双周期吸引子;(d)y-z平面双周期混沌吸引子;(e)x-y平面单周期吸引子;(f)y-z平面单周期吸引子
[1]Hartley T T,Lorenzo C F,Qammer H K 1995 IEEE Trans.Circuits Syst.-I:Fundamental Theory and Applications42 485
[2]Li CG,Chen GR 2004 Physica A 341 55
[3]Grigorenko I,Grigorenko E 2003 Phys.Rev.Lett.91 034101
[4]Ichise M,Nagayanagi Y,Kojima T 1971 J.Electroanal.Chem.33 253
[5]Bagley RL,Calico RA 1991 J.Guid.Contr.Dyn.14 304
[6]Sugimoto N 1991 J.Fluid Mech.25 631
[7]Torvik PJ,Bagley RL 1984 J.Appl.Mech.Trans.ASMF 51 294
[8]Lu JG,Chen G R 2006 Chaos,Solitonsand Fractals27 685
[9]Li CP,Guo JP 2004 Chaos,Solitonsand Fractals22 443
[10]Li CG,Chen G R 2004 Chaos,Solitonsand Fractals22 549
[11]Lu JG 2006 Phys.Lett.A 354 305
[12]Huang X,Zhao Z,Wang Z,Li Y X 2012 Neurocomputing 94 13
[13]Ge ZM,Qu CY 2007 Chaos,Solitonsand Fractals34 262
[14]Hu JB,Xiao J,Zhao LD 2011Acta Phys.Sin.60110515(in Chinese)[胡建兵,肖建,赵灵东2011物理学报60 110515]
[15]Wu CJ,Zhang Y B,Yang N N 2011 Chin.Phys.B 20 060505
[16]Chen L P,Chai Y,Wu R W,Sun J,Ma T D 2012 Phys.Lett.A 376 2381
[17]Wang Z,Huang X,Zhao Z 2012 Nonlinear Dyn.69 999
[18]Li HQ,Liao X F,Lou M W 2012 Nonlinear Dyn.68 137
[19]Liu CX 2007 Acta Phys.Sin.56 6865(in Chinese)[刘崇新2007物理学报56 6865]
[20]Chen X R,Liu CX,Wang FQ,Li Y X 2008 Acta Phys.Sin.57 1416(in Chinese)[陈向荣,刘崇新,王发强,李永勋2008物理学报57 1416]
[21]Yu Y G,Li H X,Wang S,Yu JZ 2009 Chaos,Solitons and Fractals 1181
[22]Yu SM,L¨u JH,Chen GR 2007 Phys.Lett.A 364 244
[23]Yang X S,Li Q D,Chen GR 2003 Int.J.Circ.Theor.Appl.31 637
[24]Li Y X,Tang WK S,Chen GR 2005 Int.J.Circ.Theor.Appl.33 235
[25]Jia H Y,Chen Z Q,Yuan Z Z 2009 Acta Phys.Sin.58 4469(in Chinese)[贾红艳,陈增强,袁著祉2009物理学报58 4469]
[26]Wang GY,He H L 2008 Chin.Phys.B 17 4014
[27]Wang GY,Liu JB,Zheng X 2007 Chin.Phys.16 2278
[28]Zhang Z X,Yu SM 2009 Chin.Phys.B 18 119
[29]Yu SM,Yu Z D 2008 Acta Phys.Sin.57 6859(in Chinese)[禹思敏,禹之鼎2008物理学报57 6859]
[30]Liu Y Z 2008 Acta Phys.Sin.57 1439(in Chinese)[刘扬正2008物理学报57 1439]
[31]Liu Y Z,Lin CS,Li X C 2011 Acta Phys.Sin.60 060507(in Chinese)[刘扬正,林长圣,李心朝2011物理学报60 060507]
[32]Charef A,Sun Y Y,Tsao Y Y 1992 IEEE Trans.Autom.Control 37 1465
[33]Ahmad WM,Sprott JC 2003 Chaos,Solitonsand Fractals16 339

