求解非线性方程组的蛙跳和BFGS混合算法

潘 学

(广西民族大学教务处，广西 南宁 530006)

0 引言

在工程计算中，非线性方程组的求解问题是最常见的问题之一，如在数值天气预报、石油地质勘探、计算生物化学、控制领域和轨道设计等方面均有应用。因此，寻找高效可靠的非线性方程组的求解方法是非常有必要的［1-2］。目前，求解非线性方程组主要有两种途径:一种是采用传统的数值求解方法，比如牛顿迭代法、梯度下降法、BFGS方法和它们的改进算法等［3］。这些方法具有较高的求解精度和较快的收敛速度，但对初始值非常敏感，如果选取的初始值不在这些传统方法的收敛域内，这些方法将失效［4］。另一种是采用群智能优化算法，如遗传算法、模拟退火算法、差分进化算法和人工鱼群算法［5-6］等。这些算法的优点是对函数本身没有要求，对初始值不敏感，但容易陷入局部最优，导致求解精度不高。

2003 年，美国学者 Eusuff和 Lansey［7］借鉴粒子群优化算法的思想，将种群的个体看作青蛙，通过模拟青蛙在觅食过程中共享最优信息的行为，提出了一种新的群智能优化算法—混合蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)。SFLA是一种受自然生物启示而产生的基于群体协同搜索的优化方法，具有概念简单、参数少、计算速度快、易于实现等优点。目前，SFLA已被成功运用到解决贴片机贴装顺序优化问题、组合优化和数值优化等领域［8-9］。随着研究的深入，学者们发现，与其他群智能优化算法一样，蛙跳算法也存在早熟收敛和求解精度不够高的缺点［10］。为了提高蛙跳算法的优化性能，学者们提出了很多的改进算法。比如，赵鹏军等人［11］在子群内部搜索中结合吸引排斥机制，有效避免了算法早熟收敛的问题;何兵等人［12］将蛙跳算法和差分进化算法进行融合，提出了一种蛙跳和差分进化混合算法，提高了算法的性能;葛宇等人［13］将Logistic混沌序列引入到蛙跳算法中，提出了自适应混沌变异蛙跳算法，并用实验证明了该算法的有效性，等等。这些改进算法在一定程度上提高了蛙跳算法的性能，但是仍然有各自的不足。

基于以上的分析，本文在利用蛙跳算法求解非线性方程组时，引入具有强局部收敛能力的BFGS算法，以提高蛙跳算法的局部细化搜索能力，进而提高算法的求解精度。仿真实验结果表明，本文提出的蛙跳和BFGS混合算法在解决非线性方程组方面效果显著，其求解精度比已有的一些求解方法的求解精度高，是求解非线性方程组的有效方法。

1 模型的建立

实函数非线性方程组的一般形式(假设有n个变量 x1，x2，...，xn和 n 个方程，且有解)为:

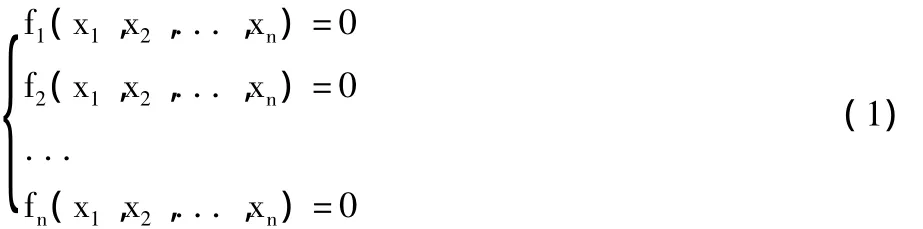
一般地，方程组(1)式可以转化为如下的最优化问题形式:

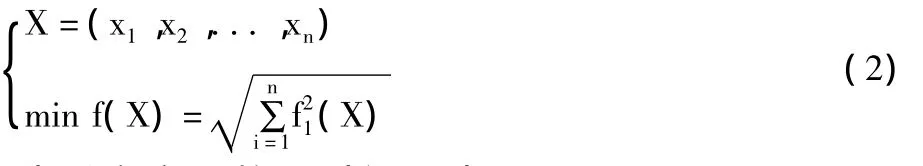
则构造适应度函数可以设置为:

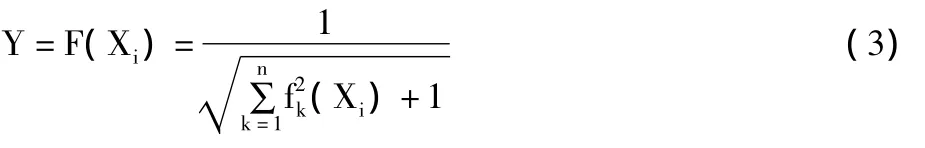
则求解非线性方程组(1)的问题就转化为求适应度函数Y最小值的优化问题。

2 蛙跳和BFGS混合算法

2.1 混合蛙跳算法的基本理论

混合蛙跳算法是一种群体智能进化算法，它模拟青蛙群体寻找食物时按子群分类进行信息交换的过程，将全局搜索与子群内部搜索相结合，使算法能朝全局最优解方向进化。混合蛙跳算法的数学模型如下:

设青蛙群体规模为F，其中第i个个体在D维空间中的坐标为xi=(xi1，xi2，…，xiD)，计算个体的适应度f(xi)，根据适应度将其按升序顺序排列存储于集合{(xi，fi)，i=1，2，…，F}中，然后按照特定的划分原则将整个青蛙群体分为S个子群{Y1，Y2，…，Ys}，每个子群中包含N个个体，即满足关系F=SN。族群划分规则为:

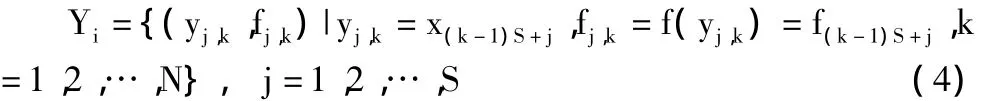
在每一个子群中，适应度最优的解记为 xb=(xb1，xb2，…，xbD)，适应度最差的解记为 xw=(xw1，xw2，…，xwD);群体中适应度最优的解记为xg=(xg1，xg2，…，xgD)。则在每次进化中，对xw进行更新操作，其搜索策略为:

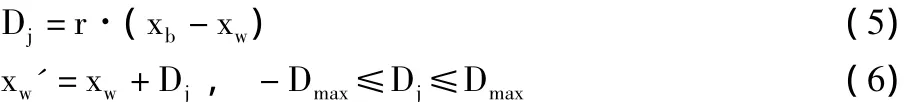
其中，r为［0，1］内的均匀随机数，j=1，2，…，S，Dmax为最大移动步长。如果f(xw')优于f(xw)，则用xw'代替xw;若没有改进，则用xg替换xb，重复执行式(5)和式(6);如若仍没有改进，则从搜索空间中随机产生一个新的解代替原来的xw，并在指定迭代次数内继续执行以上操作。随后对所有族群的青蛙重新混合并排序，更新群体最佳青蛙位置xb，然后重新划分族群，如果循环直到满足终止条件，从而完成了蛙跳算法的进化过程。

2.2 BFGS 方法

BFGS 方法［14］是由 Broyden、Fletcher、Goldfarb 和Shanno等人在1970年提出的。它是一个拟牛顿方法，具有二次终止性、整体收敛性和超线性收敛性，且算法所产生的搜索方向是共轭的。BFGS方法是一个有效的局部算法，用来求解优化问题的主要步骤如下:

其中，Step5中不精确一维搜索方法使用的是Wolfe不精确一维搜索方法，即要求λk满足:

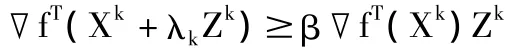
其中，α =0.1，β =0.5。

2.3 蛙跳和BFGS混合算法的过程

混合蛙跳算法具有良好的全局搜索能力，并具有对初始值、参数选择不敏感、鲁棒性强和容易实现等优点，是一种较好的全局优化方法。但在优化后期混合蛙跳算法的收敛速度有所变慢，而且求解精度不高，这是因为混合蛙跳算法缺乏良好的局部细化搜索能力，导致搜索结果仅获得满意解域而不是最优解。为了克服这些缺点，本文在混合蛙跳算法的进化后期阶段引入BFGS方法，利用BFGS强的局部搜索能力和超收敛性来加快收敛速度，提高算法整体的局部搜索能力，进而提高求解精度。由于BFGS是局部搜索算法，其优化结果的好坏在很大程度上取决于初始值的选取，为此可以利用具有全局有所能力较强的混合蛙跳算法提供给BFGS方法良好的初始值。

设群体中解的个数为M、子群数为S、最大子群内部进化代数为P以及最大全局进化代数为G，适应度函数为f(x)。针对最小值函数优化问题，本文提出的蛙跳和BFGS混合算法的伪代码如下:

3 实验结果与分析

为了测试本文算法求解非线性方程组的性能，采用蛙跳和BFGS混合算法对3个非线性方程组［15］进行测试，测试结果和几种传统的数值方法以及混合蛙跳算法的结果进行比较。所有实验均在Intel(R)Core(TM)2 Duo CPU E4500、2G 内存和 MATLAB 7.11.0的环境中运行。算法中涉及的参数设置如下:种群中解个数M=300，子群数S=30，子群内解个数N=10，子群内部进化代数P=25，BFGS的最大迭代次数K=10，ε=1E－7。为了减小误差，本文算法的最后结果是算法独立运行20次的平均值。实验结果如表1～表3所示，图1和图2分别是基本混合蛙跳算法和本文算法对第一个非线性方程组和第二个非线性方程组的计算误差的对比图。

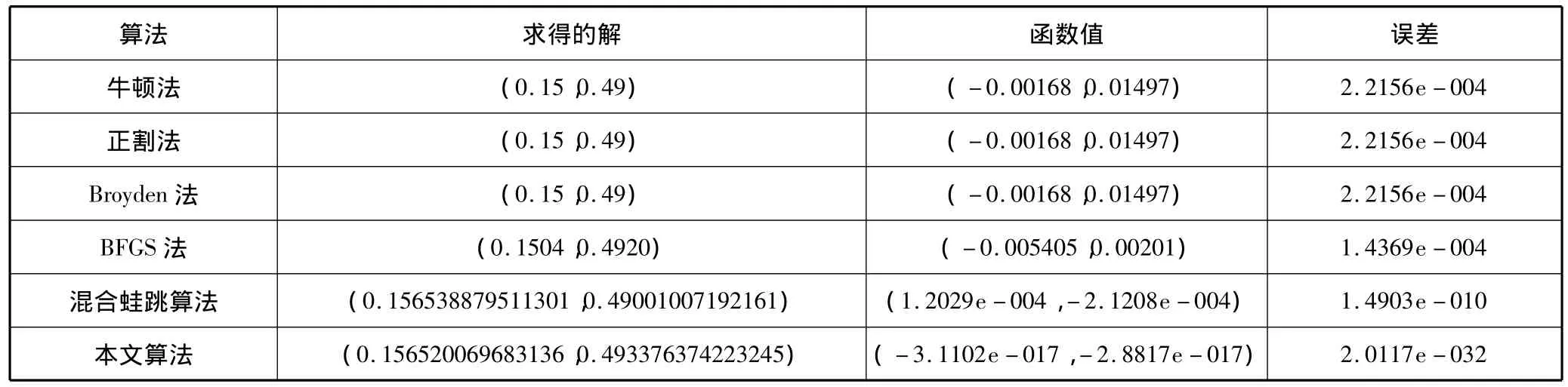
表1 第一个非线性方程组的求解结果

表2 第二个非线性方程组的求解结果

表3 第三个非线性方程组的求解结果

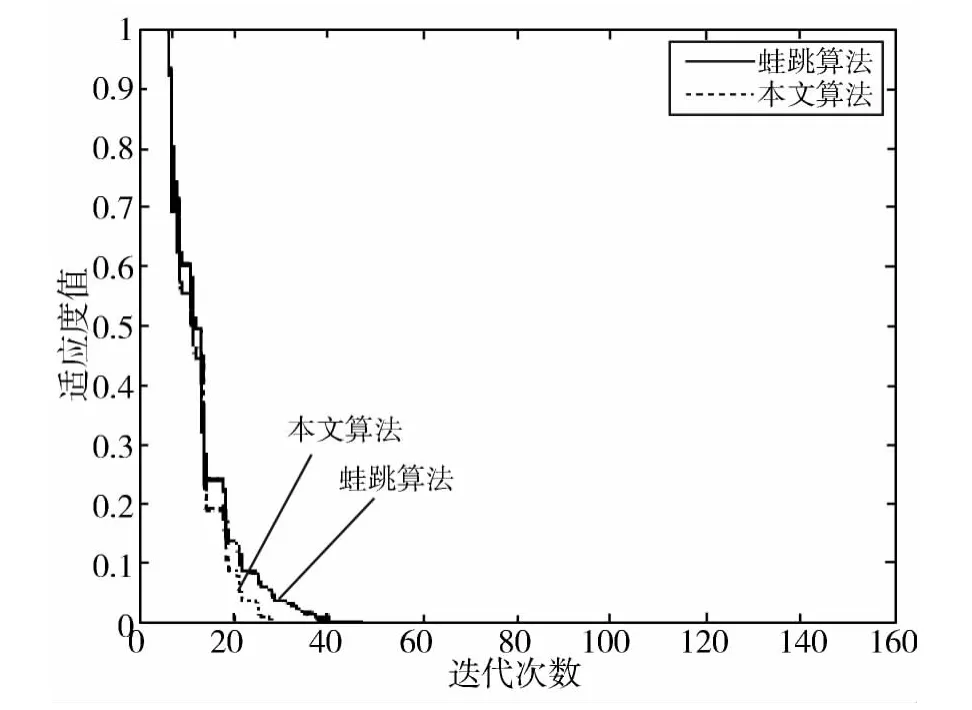
图1 对第一个非线性方程组的计算误差对比图

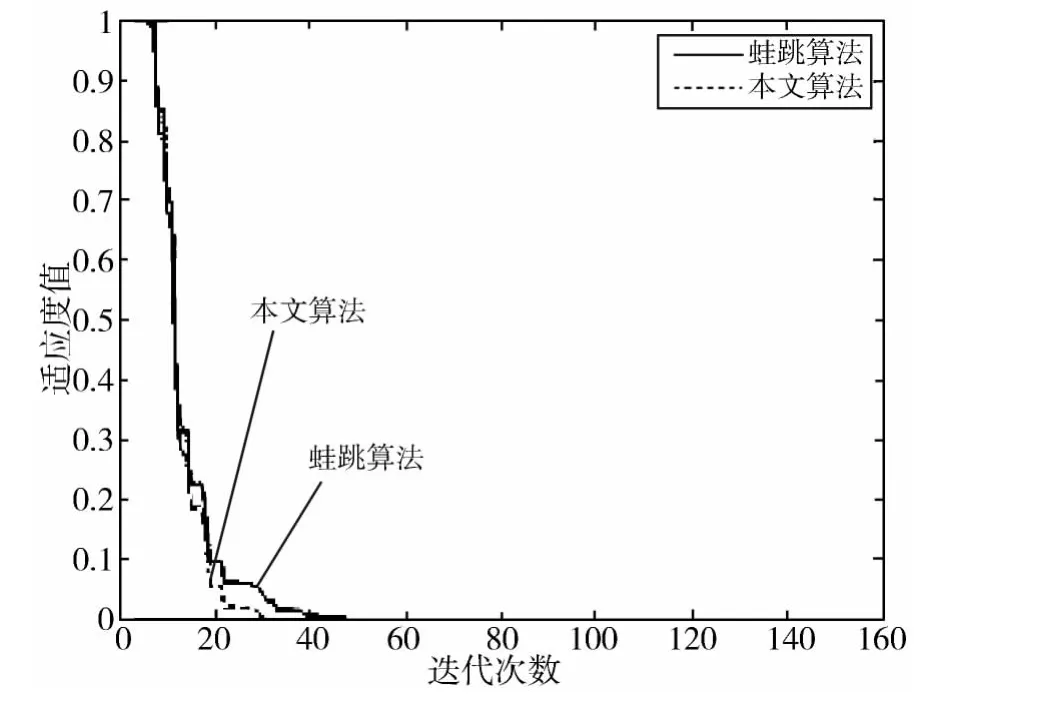
图2 对第二个非线性方程组的计算误差对比图

从表1可以看出，对于第一个非线性方程组，前面4种传统算法的计算结果相差不大，误差基本上是1E－4。而基本混合蛙跳算法的计算结果比传统算法的结果要好，误差降到了1E－10，而本文算法的计算误差达到1E－32，比基本混合蛙跳算法的误差降低了3倍。这表明，对于第一个非线性方程组，本文的计算精度比其它算法提高了很多。图1是基本混合蛙跳算法和本文算法对第一个非线性方程组的计算误差对比图，从图中可以看出，本文算法的收敛速度比基本混合蛙跳算法的收敛速度快。对于第二个非线性方程组，表2的实验结果表明，本文算法的误差结果达到了0，这说明本文算法获得了精确解，而其它算法却没有达到这个精度。图2是第二个非线性方程组的计算误差图，从图2也可以看出，本文算法的收敛速度比基本混合蛙跳算法的收敛速度快。第三个方程组包含10个方程，从表3可以看出，相对于传统算法，混合蛙跳算法和本文算法的计算误差要小很多，特别本文算法，误差比基本混合蛙跳算法降低了1倍。

3个经典的非线性方程组的实验结果表明，与传统算法和基本混合蛙跳算法相比，本文算法能用更少的迭代次数找到更精确的解，计算精度有所提高。

4 结束语

为提高蛙跳算法的局部细化能力，进而提高其计算精度，引入局部搜索能力强的BFGS算法，提出一种蛙跳算法和BFGS的混合算法。该混合算法较好地利用了蛙跳算法强的全局搜索能力和BFGS强的局部细化能力，不但可以加快算法的收敛速度，而且有效地提高了搜索精度，具有很强的鲁棒性。3个非线性方程组的实验结果表明，该方法是一种较好的求解非线性方程组的算法，能获得比传统算法和基本蛙跳算法更好的求解精度和收敛速度。

［1］王冬冬，周永权.人工鱼群算法在求解非线性方程组中的应用［J］.计算机应用研究，2007，24(6):242-244.

［2］陈海霞，杨铁贵.基于极大熵差分进化混合算法求解非线性方程组［J］.计算机应用研究，2010，27(6):2028-2030.

［3］Li D H，Fukushima M.A modified BFGS method and its global convergence in nonconvex minimization［J］.Journal of Computational and Applied Mathematics，2001，129(1-2):15-35.

［4］付振岳，王顺芳，丁海燕，等.并发遗传退火算法求解复杂非线性方程组［J］.云南大学学报:自然科学版，2012，34(1):15-19.

［5］刘利斌，欧阳艾嘉，许卫明，等.求解非线性方程组的BFGS差分进化算法［J］.计算机工程与应用，2011，47(33):55-58.

［6］高雷阜，齐微.改进的粒子群理论及在非线性方程组中的应用［J］.计算机工程与应用，2011，47(35):48-50，76.

［7］Eusuff M M，Lansey K E.Optimization of water distribution network design using the shuffled forg leaping algorithm［J］.Journal of Water Resources Planning and Management，2003，129(3):210-225.

［8］万博，卢昱，陈立云，等.求解CVRP的改进混合蛙跳算法研究［J］.计算机应用研究，2011，28(12):4503-4506.

［9］陈铁梅，罗家祥，胡跃明.基于蚁群-混合蛙跳算法的贴片机贴装顺序优化［J］.控制理论与应用，2011，28(12):1813-1820.

［10］丁卫平，王建东，管致锦.基于量子蛙跳协同进化的粗糙属性快速约简［J］.电子学报，2011，39(11):2597-2603.

［11］赵鹏军.基于差分扰动的混合蛙跳算法［J］.计算机应用，2010，30(10):2575-2577.

［12］何兵，车林仙，刘初升.一种蛙跳和差分进化混合算法［J］.计算机工程与应用，2011，47(18):4-8.

［13］葛宇，王学平，梁静.自适应混沌变异蛙跳算法［J］.计算机应用研究，2011，28(3):945-947.

［14］唐焕文，秦学志.实用最优化方法［M］.大连:大连理工大学出版社，2006.

［15］Grosan C，Abraham A.A new approach for solving nonlinear equations systems［J］.IEEE Transactions on Systems，Man and Cybernetics-Part A，2008，38(3):698-714.