Stability criteria for neutral delay differential-algebraic equations

FAN Ni，LIU Lingling，SUN Leping

(College of Mathematics and Sciences，Shanghai Normal University，Shanghai 200234，China)

1 Introduction

Functional differential equations have a wide range of applications in science and engineering．Delay differential equations(DDEs)，in which the delayed argument occurs in the state variable but not in their derivative，are the simplest and perhaps most natural type of function differential equations．Delay differential-algebraic equations(DDAEs)，which have both delay and algebraic constraints，arise in a wide variety of scientific and engineering applications．Neutral delay differential-algebraic equations(NDDAEs)are a kind of DDAEs with more complicated structure since they not only have delay terms but also have the derivatives of the delay terms．In this paper we are concerned with the asymptotic stability of a general system of NDDAEs

Ax′(t)+Bx(t)+Cx′(t- τ)+Dx(t- τ)=0 ，where A，B，C，D∈Rd×dare constant real matrices，A is singular and τ＞0 stands for a constant delay．We shall study delay dependent criteria for the above system．Our stability criteria only require the evaluation of a real function on the boundary of a certain region in the complex plane．The region is given as the intersection of a rectangle and a half circle both specified with the system．

We will introduce the zeros of an analytical function in a bounded region in Section 2 and the logarithmic norm of a matrix in Section 3．In the last Section，two stability criteria of NDDAEs are presented．

2 Preliminary

As a preliminary，we introduce some theorems on complex-variable functions．Let W denote a bounded region of the complex plane，and ∂W and W— represent the boundary and the closure of W，respectively．That is，W— =∂W∪W．

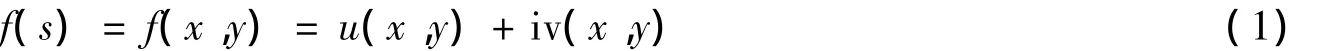
is an arbitrary analytical function for s∈W—．Here i2= －1，s=x+i y，u(x，y)=Re f(s)，v(x，y)=Im f(s)．The following two theorems give sufficient conditions for non-existence of zeros of f(s)∈W—．The two theorems only require the evaluation on the boundary ∂W of harmonic functions each corresponding to f．Hence they are called the boundary criteria．

Theorem 2．1［1］If for any(x，y)∈∂W，the real part u(x，y)in(1)does not vanish，then f(x，y)≠0 for any(x，y)∈W．

Theorem 2．2［1］Assume that for any(x，y)∈∂W，there exists a real constant λ satisfying u(x，y)+λv(x，y)≠0．Then f(s)=u(x，y)+i(x，y)≠0 for any(x，y)∈W—．

Theorem 1．2 is an extension of Theorem 1．1．

3 Delay independent stability of NDDAEs

Now we deal with the asymptotic stability of NDDAEs，

where A，B，C，D∈Rd×dare constant real matrices，A is singular and τ＞0 stands for a constant delay．For the stability of the system(2)，we investigate its characteristic equation

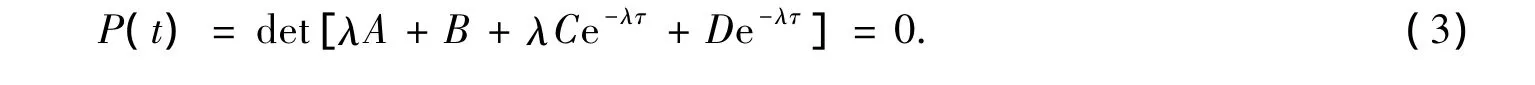
where z=x+i y．By the above assumption that Re s＜0⇔Reλ ＜0 is valid．

The following two lemmas are well-known．

Lemma 3．1［2］If the real parts of all the characteristic roots of(5)are less than zero，then the system(2)is asymptotically stable．That is，the solution x(t)of(2)satisfies x(t)→0 as t→∞ ．

Lemma 3．2［3］Let A ∈Cd×dand B ∈Rd×d．If the inequality≤B holds，then the inequality ρ(A)≤ρ(B)is valid．Here the order relation of matrices of the same dimensions should be interpreted componentwise．stands for the matrix whose component is replaced by the modulus of the corresponding component of A，and ρ(A)means the spectral radius of A．

For a complex matrix W，letμ(W)be the logarithmic norm of W．μ(W)depends on the chosen matrix norm．Letdenote the matrix norm of W subordinate to a certain vector norm．In order to specify the norm，the notationis used．And the notation μp(·)is also adopted to denote the logarithmic norm associated with

Lemma 3．3［3］For each eigenvalue of a matrix W∈Cd×d，the inequality

holds．

Lemma 3．4［4］Let U，V be n × k rectangular matrices with k≤n，and A be an n × n matrix．Then

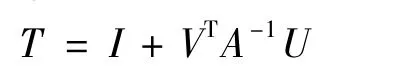
is nonsingular if and only if A+UVTis nonsingular．In this case，we have

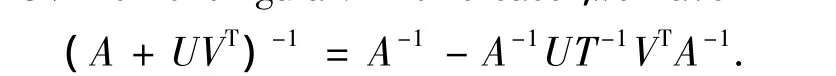
Lemma 3．5［4］Letbe a norm defined on Cn×nwith=1 and A∈Cn×nsatisfy＜1．Then I－A is nonsingular and satisfies

The following lemma states a sufficient condition for the stability of(2)．

Proof Assume that the condition of the lemma is satisfied and that the system(2)is unstable．There is a characteristic root of(5)with positive real part．Note that the characteristic root is an eigenvalue of the ma-

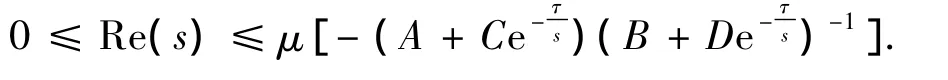
Applying the properties of the logarithmic norm，Lemma 2．4 and Lemma 2．5，we have

This，however，contradicts the condition．Hence the proof is completed．

The following theorem gives a region including all the roots of(5)with nonnegative real parts when the condition of Lemma 2．6 fails．

Theorem 3．1 Let B－1· D ＜1．Suppose that there exists a root of(5)whose real part is nonnegative．

(i)If we have the estimation

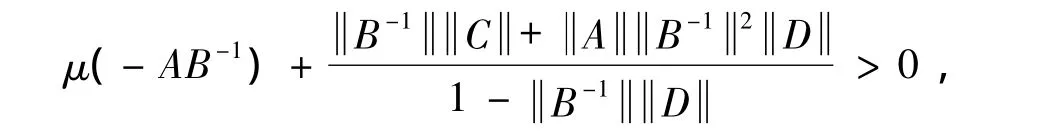
then the inequalities

hold．

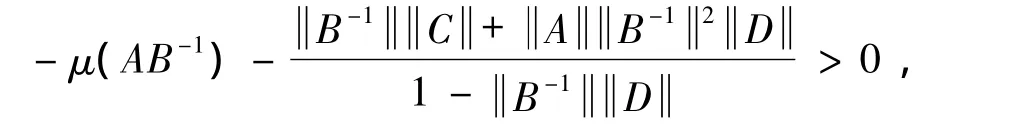
(ii)If we have the estimation define a positive numberβsatisfying

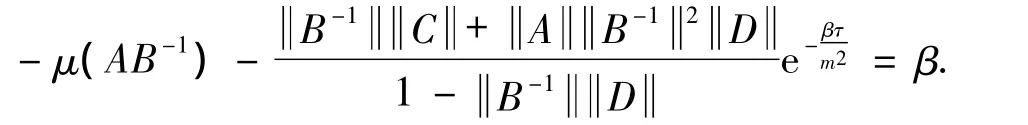
Then the inequalities and

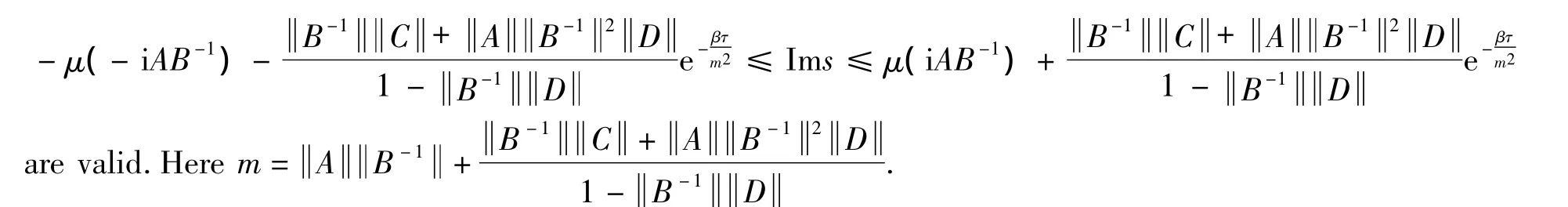
Proof (i)A discussion similar to that of Lemma 2．6 yields

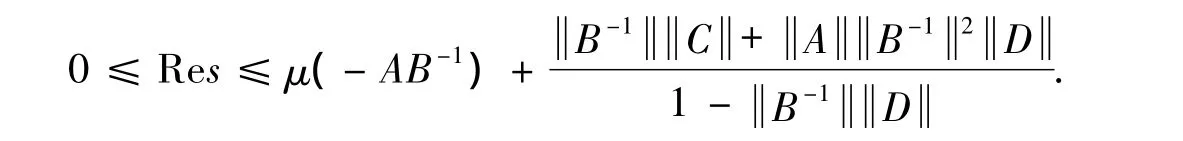
Noting that the imaginary part of an eigenvalue of a matrix A is equal to the real part of an eigenvalue of－i A，we have the second inequality．

(ii)By Lemma 2．3

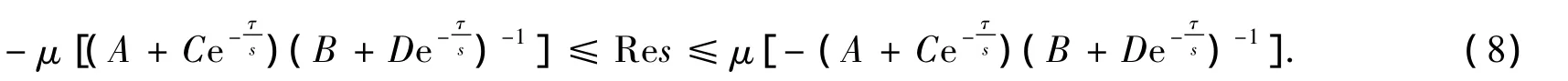
A derivation similar to that of Lemma 2．6 leads to

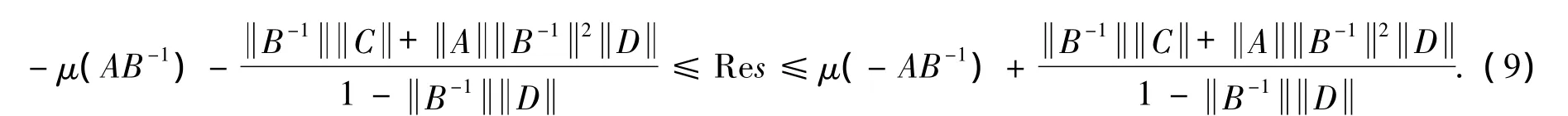
Letβ0= －μ(AB－1)－B－1C+AB－12D1－B－1D．The inequality(8)implies

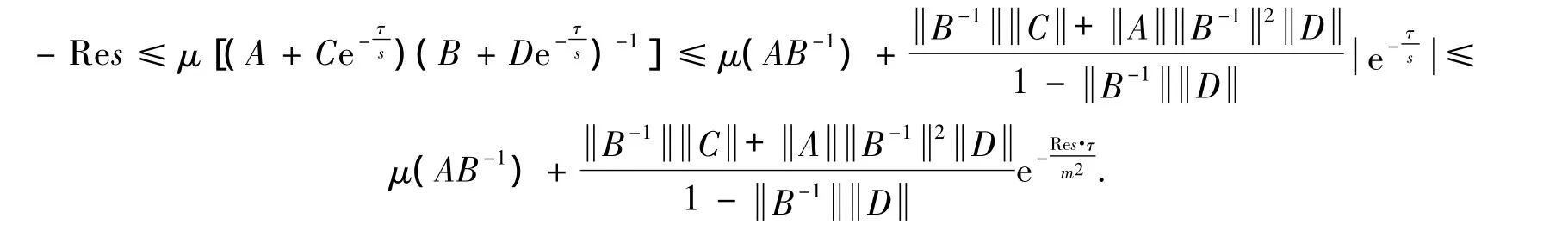
Here the truth of the last inequality is attained from the following．

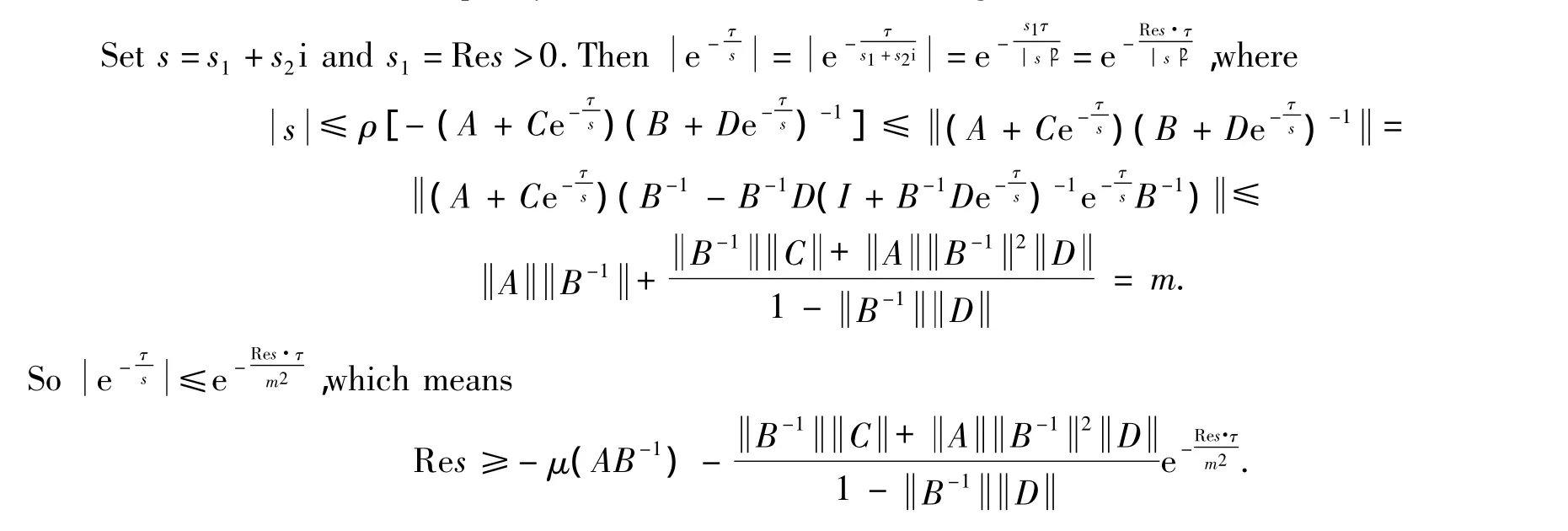
Hence，taking(9)into consideration，we have

Iteration

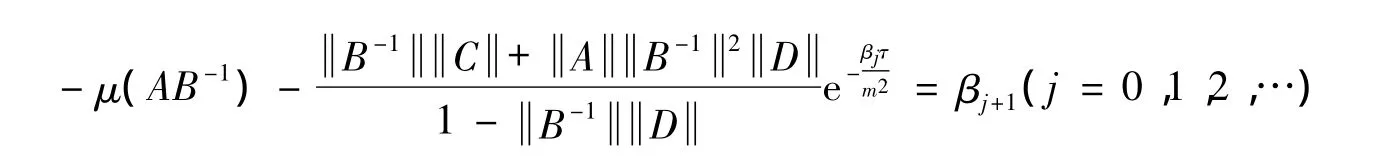
and the monotonicity

ensure that the limit of the series{βj}is equal toβ，whereβ is a positive number satisfying

Therefore the first inequality holds．In a similar manner we can get the second inequality．

Theorem 3．2 Let B－1· D ＜1．If s is a characteristic root of(6)with nonnegative real part，then the inequality

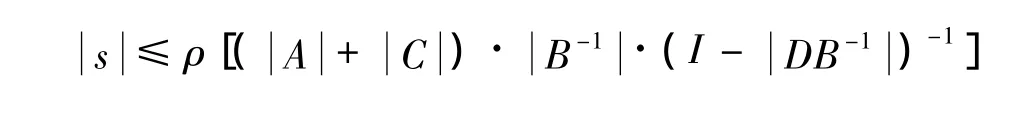
holds．

Proof By the assumption above，there exists an integer j(1≤j≤d)such that

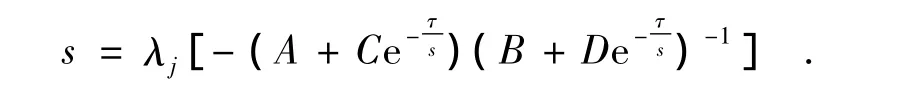
This implies the inequality

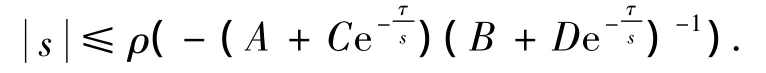
It is obvious that

Due to Lemma 2．2，we have the conclusion．

4 Boundary criteria for NDDAEs

By virtue of Lemma 2．6，ifγ ＜0，the system(2)is asymptotically stable．Ifγ≥0，the system(2)may be stable or unstable．We consider the stability of(2)when γ≥0．

Letβ0= － μ(AB－1)and γ≥0．we define the following quantities according to the sign ofβ0．(See Theorem 2．1)

(i)Ifβ0≤0，then we put

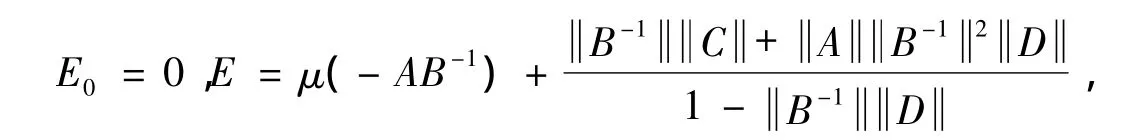
F0=-μ(-i AB-1)

(ii)Ifβ0＞0，then we put

whereβis a root of the equation

Under the above notation we turn our attention to the following three kinds of bounded regions in the s-plane．

Definition 1 Let l1，l2，l3and l4denote the segments{(E0，y)∶F0＜ y ＜ F}，{(x，F)∶E0≤x≤E}，{(E，y)∶F0≤y≤F}and{(x，F0)∶E0≤x≤E}，respectively．Furthermore，l=l1∪l2∪l3∪l4and let D be the rectangular region surrounded by l．

Definition 2 Let R= ρ［(A + C)· B－1·(I－ DB－1)－1］．Let K denote the circular region with radius R centered at the origin of the plane of C．

Definition 3 Let T represent the intersection D∩K．The boundary of T is denoted by ∂T and T—=T∪∂T．

A necessary and sufficient condition for the delay-independent stability of the system(2)is presented in［5］．The following two theorems give criteria for the delay-dependent stability of the system(2)．We apply Theorem 1．1 and Theorem 1．2 to prove them respectively．

Theorem 4．1 If for any(x，y)∈∂T，the real part U(x，y)in(6)does not vanish，then the system(2)is asymptotically stable．

Proof Assume that the condition is satisfied and that the system(2)is unstable．This means the existence of a characteristic root of(6)with nonnegative real part．According to Lemma 2．1．It suffices to prove P(s)≠0 for Re s≥0．Because of Theorem 2．1 and Theorem 2．2 and Definition 3，it is sufficient to consider s∈T—．

From the assumption of this theorem and the statement of Theorem 1．1，this contradicts that P(s)=0 for s∈T—．Hence P(s)≠0 for Re s≥0 and the proof is completed．

Due to Theorem 1．2，we can further extend the above result as follows．

Theorem 4．2 Assume that for any(x，y)∈∂T，there exists a real constantλ satisfying

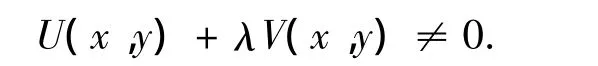
Then the system(2)is asymptotically stable．

The proof is analogous to Theorem 3．1．

We give two criteria for the delay-dependent stability of the linear delay system(2)．Theorem 2．1 and Theorem 2．2 show that the unstable characteristic roots of the system(2)are located in some specified bounded region in the complex plane，while Theorem 3．1 and Theorem 3．2 show that it is sufficient to check certain conditions on its boundary to exclude the possibility of such roots from the region．Theorem 1．1 and Theorem 1．2 provide general and simple criteria for the nonexistence of zeros of an analytic function in any boundary region．

［1］HU G D．Stability of discrete-delay systems:boundary criteria［J］．Applied Mathematics and Computation，1996，80:95－104．

［2］KUANG J X，TIAN H J．The asymptotic behaviour of theoretical and numerical solution for the differential equations with several delay terms［J］．Journal of Shanghai Normal University(Natural Sciences)，1994，23:1 －9．

［3］DESOER C A，VIDYASAGAR M．Feedback system:input-output properties［M］．New York:Academic Press，1997．

［4］GOLUB G，VAN LOAN C F．Matrix computations［M］．3rd edition，Baltimore:Johns Hopkins University Press，1996．

［5］QIU L，KUANG JX．On the LD-stability of the nonlinear systems in MDBMs［J］．Journal of Shanghai Normal University(Natural Sciences)，1996，25(4):6 －11．

［6］HU G D，MITSUI T．Stability of linear systems with matrices having common eigenvectors［J］．Japan J Indust Appl Math，1996，13:487 －494．

［7］LU L H．Numerical stability of the θ-methods for systems of differential equations with serveral delay terms［J］．Journal of Computational and Applied Mathematics，1991，34:292 －304．

［8］SUN L P．The Pm-stability of multistep runge-kutta methods for delay differential equations［J］．Journal of Shanghai Normal University:Natural Sciences，1997，26(4):17 －22．