利用VB解决不同坐标系的变换问题

孙瑞举

(山东正元地理信息工程有限责任公司，山东济南250101)

一、引 言

坐标变换在测绘学科中应用广泛，自2008年我国启用2000国家大地坐标系后，要求把以往的1954北京坐标系、1980西安坐标系下的各类测绘成果转换成2000国家大地坐标系，这就涉及到坐标系的变换问题。

二、二维坐标的转换

点的二维坐标可以用向量［x y］T表示，假设某点坐标转换前后的坐标分别为［x1y1］T和［x2y2］T，则二维坐标的坐标转换公式为

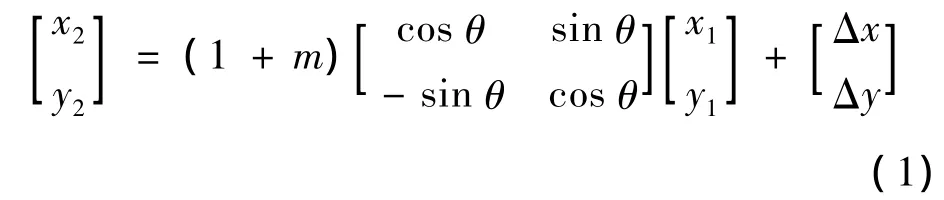
式中，m为坐标尺度参数，表示坐标转换前后坐标系的尺度变化情况;θ为坐标旋转角，表示转换后的坐标系绕前一个坐标系逆时针旋转的角度;Δx，Δy为平移参数，表示坐标原点的平移量。

在实际工作中坐标转换参数都是未知的，需要根据一定数量的具有新旧坐标的控制点来求得。为了计算方便，将式(1)改写为如下形式

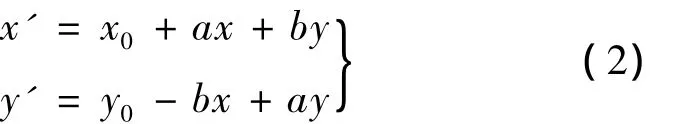
式中，x0和y0为平移量;a=k·cosθ;b=k·sinθ;k=1+m。

假设有n个控制点，其转换前的坐标分别为(x1，y1)，(x2，y2)，…，(xn，yn)，转换后的坐标为(x1'，y1')，(x2'，y2')…(xn'，yn')，根据式(2)可以列出如下方程

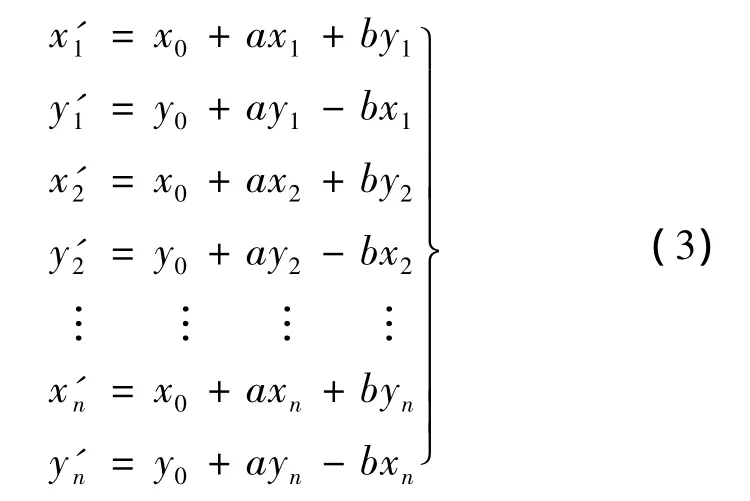
写成矩阵形式为

式中，

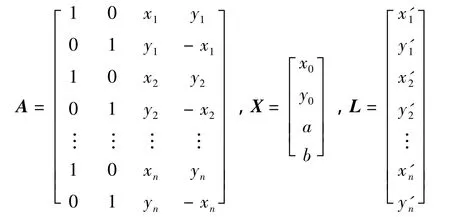
式中有4个未知量，当n=2时，有唯一解;当n＞2时，可以求得最小二乘解

三、三维坐标的转换

三维坐标转换的情况与二维坐标转换类似，也是通过尺度参数、旋转角参数和平移参数来确定，只是旋转角有3个分别绕x轴旋转、绕y轴旋转和绕z轴旋转的旋转角，平移参数也有3个，三维坐标的坐标转换公式为

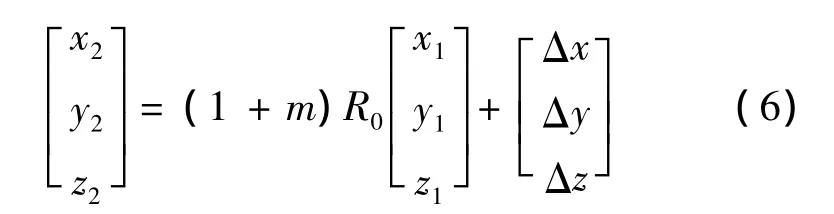
式中，m为坐标尺度参数，表示坐标转换前后坐标系的尺度变化情况;Δx，Δy，Δz为平移参数，表示坐标原点在3个方向的平移量。

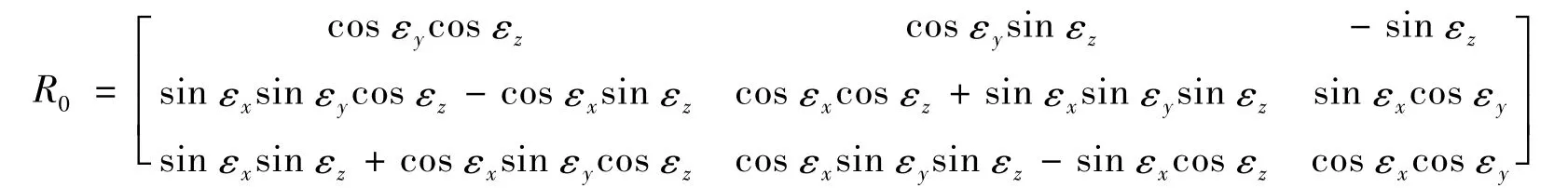
角度很小时取

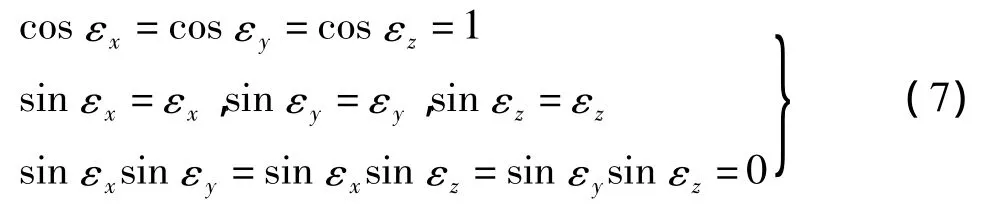
于是式(7)可以简化为

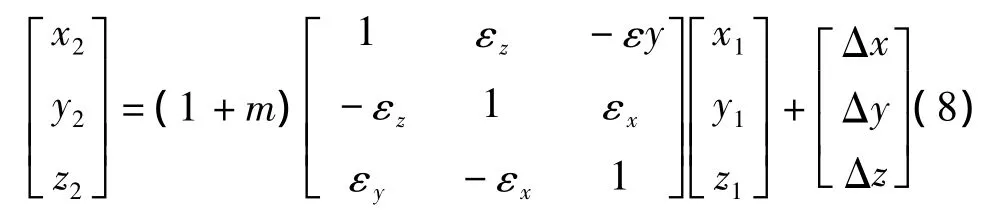
假设有n个控制点，其转换前的坐标分别为(x1，y1，z1)，(x2，y2，z2)，…，(xn，yn，zn)，转换后的坐标为(x'1，y'1，z'1)，(x'2，y'2，z'2)，…，(x'n，y'n，z'n)，根据式(8)可以列出如下方程

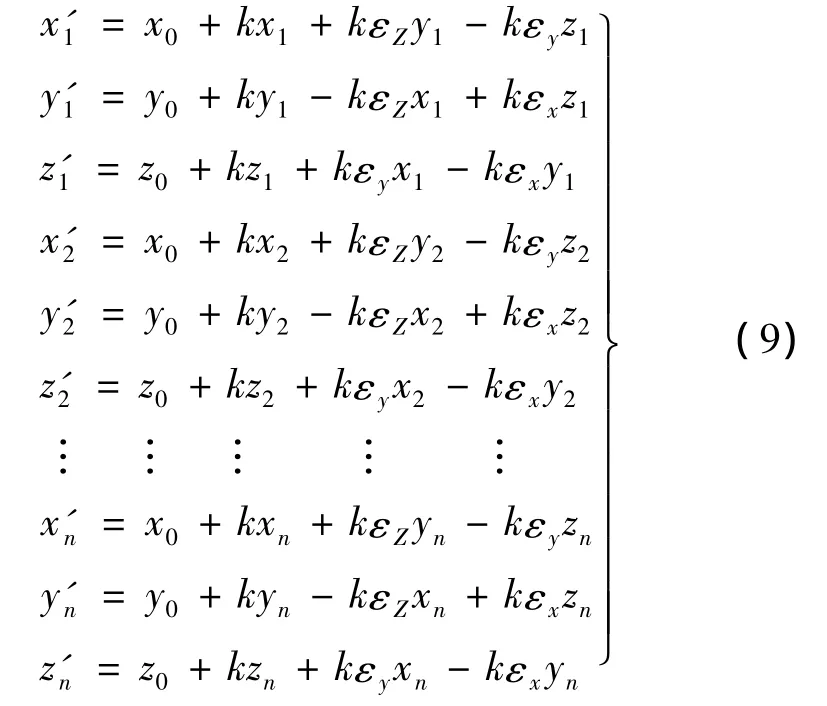
写成矩阵形式为

式中

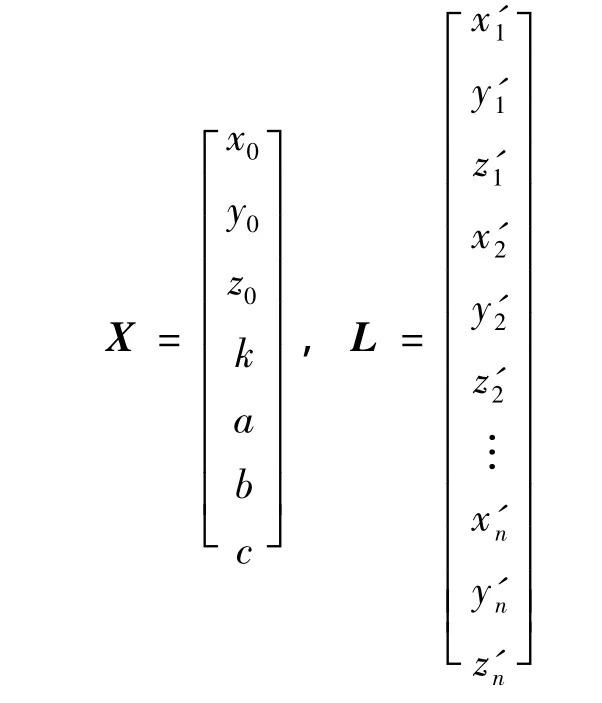
式中，k=1+m，a=kεx，b=kεy，c=kεz

式中有7个未知量，当n=3时，有唯一解;当n＞3时，可以求得最小二乘解

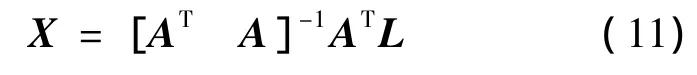
四、求解转换参数

通过上面的推导，已得到通过n个控制点来求解二维和三维坐标的转换参数公式，即式(5)和式(11)。下面我们讨论如何利用VB来求解参数，即线性方程组求解。求解线性方程组是测量程序设计中的经常遇到的问题，本次讨论的求解方法是直接法中的列选主元Guass约化法。求解转换参数的编程思路如下:

1)通过读取控制点坐标得到系数项矩阵A及常数项矩阵L，用数组A()和L()表示。

2)求得系数矩阵A的转置矩阵AT，用数组At()表示。

3)编写矩阵相乘的通用程序，得到AT·A的矩阵(用数组Aaa()表示)，及得到AT·L的矩阵(用数组Atl()表示)。

4)编写列选主元Guass约化法求解线性方程组的通用过程，来求得未知量

5)根据未知量得到二维或三维坐标的转换参数。

五、列选主元Guass约化法求解的数学过程

本程序的难点是列选主元Guass约化法的通用程序的编写，下面我们讨论其求解思路。

1.Gauss约化法

对于一般的线性方程组

式中，

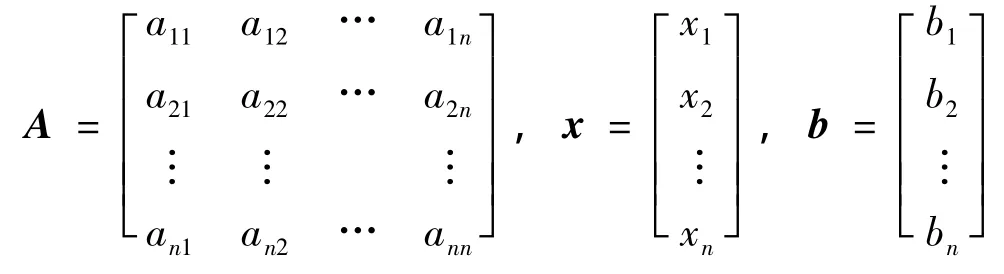
使用Gauss约化法求解，就是将上述方程组通过n-1步约化，转化为上三角方程组

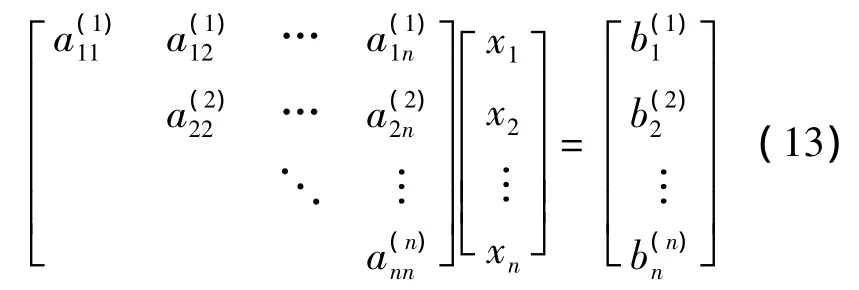
再回代，求此方程组的解。

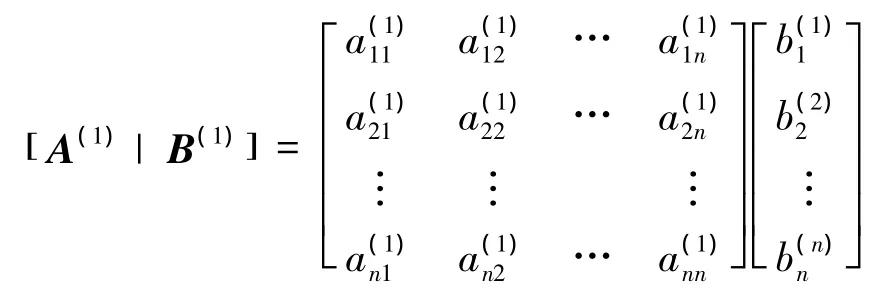
则方程组得Gauss约化的具体步骤是

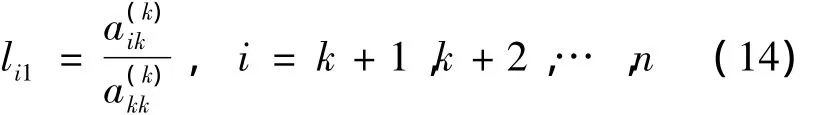
用―lik乘第1行再加到第k行，可以消去，具体公式是

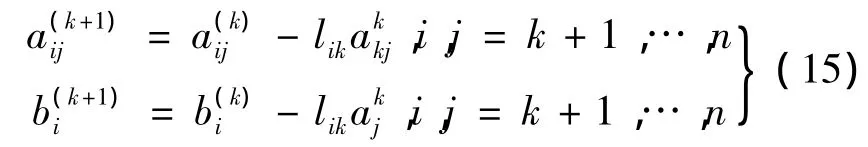
4)将其直接回代得

即可以求出线性方程组的解。

2.列选主元Gauss消去法

六、列选主元Guass约化法求解的VB序通用过程

根据上述数学求解线性方程组的过程原理，用VB编写列选主元Guass约化法求解通用过程如下:

七、结束语

实际工作中经常会遇到坐标系的变换问题，尤其是2000国家大地坐标系的使用，如何把以往坐标系的成果转换到2000国家大地坐标系，涉及的工作量大，格式不一，通过本程序可以灵活解决。

［1］孔祥元，梅是义.控制测量学［M］.武汉:武汉大学出版社，2003.

［2］佟彪.VB语言与测量程序设计［M］.北京:中国电力出版社，2007.