分数阶超混沌系统的动力学分析及同步
李贤丽,杜成龙
(东北石油大学 黑龙江 大庆 163000)
17世纪初期分数微分学就已经被人们所开始研究,尤其是在近十年,许多物理系统被发现可以表现出分数阶动力学行为,如电解液和电磁波、沾滞系统[1-3]等等,而且分数阶的性质同时也被广泛运用到生物数学、电路学、电化学与物理、工程与自动化、自动控制学等领域。与传统的整数阶微分相比,分数阶微分系统有着更为复杂的属性和结构,它可以更加优秀的描述一些实际系统。因此,分数阶系统得到越来越多的科学家的关注并且对其产生了研究兴趣。目前我们所熟知的一些分数阶微分混沌系统有分数阶 Lorenz系统[4]、分数阶Chen系统[5]、分数阶Chua混沌电路[6]等等。
虽然分数阶微分的研究已经有300多年的历史,但是在工程和物理应用中,尤其是在混沌及其同步方面一直未得到深入的应用。因此,许多学者慢慢的开始从事分数阶混沌动力系统的研究。
文中在刘明华,冯久超提出的一个新的超混沌系统[7]的基础上对其指数是分数时的形式的特性进行讨论,并且在此基础利用分数阶非线性系统稳定性理论,设计合理的控制器来实现此分数阶超混沌系统的同阶数的异结构同步,以及不同阶数的异结构同步并利用数值仿真验证该控制器的正确性。
1 分数阶微积分的定义
文中采用Caputo微分定义进行研究分数阶超混沌动力

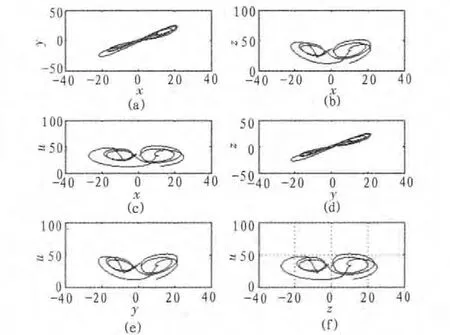
其中m为正整数,且a>0,m-1 分数阶线性系统的稳定性已经得到了充分的理论研究,并且得到了分数阶线性系统稳定的充分必要条件。 引理 自治系统 其中 X=(x1,x2,…,xn),A∈Rn×n 刘明华,冯久超提出的一个新的超混沌系统,由如下方程表示: 对应 r=35,b=3,c=35,d=8 时,他有一个奇怪吸引子。其初始状态为(10,11,12,13),平衡点为 0 点。 通过 Matlab 中的数值仿真得超混沌系统混沌吸引子相空间三维如图1所示。 图1 混沌吸引子相空间三维图Fig.1 The phase space of chaotic attractor three-dimensional figure 当前,人们给出众多分数阶微分系统的定义,下面介绍一种最常用的定义: 其中m是不小于α的最小整数,x(m)表示通常意义下的m 阶导数;Jβ(β>0)是 β 阶 Reimann-Liouville 积分算子,且 这里Γ是Gamma函数,Dα是α阶Caputo微分算子。 分数阶超混沌系统可有如下方程组表示: 其中 x1,x2,x3,x4为系统的状态变量,α 为微分阶数。 为方便比较,先讨论α为整数时的状态变量的时间响应效果。 1)当 α=1 时,设混沌系统的初始值为(10,11,12,13),利用Runge-Kutta-Felhberg算法,得出超混沌系统混沌吸引子相空间三维图1。 2)当 α<α<1时,首先讨论系统的平衡点,由论文[7]可知此混沌系统的平衡点0处的特征值如下: 根据分数阶系统稳定性理论,要使系统(4)产生混沌,则要满足 所以当0<α<1时,系统(4)时混沌的。 当 α=0.989和 α=0.777时分数超混沌系统的所对应的吸引子在x-y,x-z,x-u,y-z,y-u,z-u 平面上的投影图分别为图 2 中的 a,b,c,d,e,f和图 3 中的 a,b,c,d,e,f,混沌吸引子相空间三维图为图 4。 图2 α=0.989时分数阶超混沌系统的混沌吸引子分别在x-y,x-z,x-u,y-z,y-u,z-u 平面中的投影Fig.2 α=0.989 Hyperchaos system of chaotic attractor projection in the different plane x-y,x-z,x-u,y-z,y-u,z-u 图 3 α=0.777 时分数阶超混沌系统的 x-y,x-z,x-u,y-z,y-u,z-u 平面中的投影Fig.3 α=0.777 Hyperchaos system of chaotic attractor projection in the different plane x-y,x-z,x-u,y-z,y-u,z-u 图4 分数阶超混沌系统吸引子相空间三维图Fig.4 The phase space three-dimensional figure ofFractional order Hyperchaos system attractor 本章节主要讨论阶数相同时和阶数不同时此分数阶超混沌系统的异结构同步情况,以系统(4)作为驱动系统,响应系统为leipnik系统,如下: 1)阶数相同时分数阶超混沌系统与分数阶leipnik混沌系统的异结构同步 令驱动分数阶混沌系统为: 设计驱动系统控制器 构建 h(e)函数 根据李雅普诺夫定理,可知在控制器(7)下,分数阶混沌系统(5)和分数阶超混沌系统(6)实现了同步。基于改进的 Adams-Bashforth-Moulton理论(ABM)算法[8],对该系统进行仿真,设 x1=0.349,x2=0,x3=-0.16,x4=0,y1=10,y2=11,y3=12,y4=13图 5为 α=0.989分数阶误差系统仿真结果。 图5 α=0.989同步误差有e1,e2,e3随时间演化图Fig.5 α=0.989 synchronization error e1,e2,e3evolution figure over time 2)阶数不同情况下的分数阶超混沌系统与分数阶leipnik混沌系统的异结构同步定理1[9]设 f(t)∈Cαa([a,b]),Dαaf(t)∈Cβa([a,b]),a,β>0且m-1<β 则有,Dβa(Daaf(t))=Da+βaf(t) 将公式(5)的微分阶数设为β,则根据分数阶微分定义及定理1可得 因此分数阶不等的分数阶超混沌系统同步问题便转换为分数阶超混沌系统(4)与同阶数异结构分数阶混沌系统(8)的同步问题。 令分数阶超混沌系统(4)做驱动系统,分数阶系统(8)做响应系统。设计控制器 构建R函数 R(e)=e1(-35e1+e4)+e3(-3e3)+e4×(-e2)=-35e21-3e23≤0 根据李雅普诺夫定理可知,在控制器(9)下,设,x1=0.349,x2=0,x2=-0.16,x4=0,y1=10,y2=11,y3=12,y4=13,α=0.99,β=0.989 分数阶误差系统仿真结果如图6所示。 图6 同步误差随时间演化图Fig.6 Time evolution chart synchronization error 对一个新的超混沌系统进行分数阶形式的理论分析和数值求解,能充分了解其非线性动力学性质,并用不同方法实现分数阶系统的混沌同步,改变阶数等相关条件,分析其改变因素对分数阶混沌系统同步的影响。 [1]Samko S G,Kilbas A A,Marichey O I.Fractional integrals and derivatives[J].Theory and Applications,Gordon and breach,Yverdon,1993:121-130. [2]Grigorenko I,Grigorenko E.Chaos dynamics of the fractional Lorenz system[J].Phys Rev Lett,2003:41-61. [3]Zhou S B,Li H,Zhu Z Z.Chaos control and synchronization in a fractional neuron network system[J].Chaos Solitons and Fractals,2008,36:973-984. [4]Grigorenko I,Grigorenko E.Chaotic dynamics of the fractional Lorenz system[J].Phys Rev Lett,2003,91(3):34-101. [5]Li C G,Chen G R.Chaos in the fractional-order chen system and it’s control[J].Chaos Solitons&Fractals,2004,22(2):549-554 [6]Hartley T T,Lorenzo C F,Qammer H k.Chaos in a fractional order Chua’s system[J].IEEE Trans.Circuits Syst.I,1995,42(8):485-490. [7]刘明华,冯久超.一个新的超混沌系统[J].物理学报,2009(6):44-57.LIU Ming-hua,FENG Jiu-chao.A new hyperchaotic system[J].Acta Phys.Sin,2009(6):44-57. [8]Mohammad S T,Mohammad H.A necessary condition for double scrollattractor existence in fractional-order systems[J].Physics Letters A ,2007,367(1-2):102-113. [9]胡建兵,肖建,赵灵东.阶次不等的分数阶混沌系统同步[J].物理学报2011:11-60.HU Jian-bing,XIAO Jian,ZHAO Ling-dong.Synchronizing fractional chaotic systems with different orders[J].Acta Phys,2011:11-60.2 分数阶线性系统的稳定性理论

3 一个新超混沌系统的简介


4 分数阶超混沌系统的分析


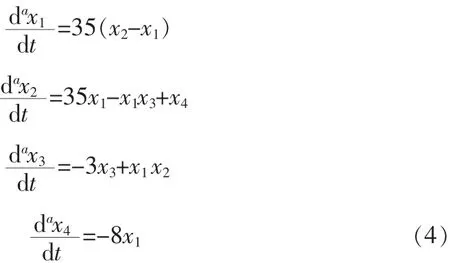



5 分数阶超混沌系统的自适应同步

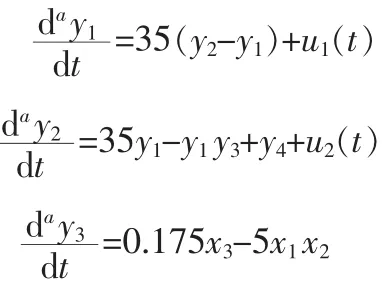







6 结论

