基于振幅方程组的行波对流的数值模拟

王卓运，宁利中，王娜，李开继

(西安理工大学 陕西省西北旱区生态水利工程国家重点实验室，陕西 西安 710048)

对流现象不仅在日常生活中很常见，同时也是自然界中很普遍的现象，比如：引起天气、气候变化的大气环流、海洋环流，引起大陆板块漂移的地幔对流，决定地磁场产生和变化的外地核对流等[1]。这些对流现象都涉及到了Rayleigh-Benard对流系统。Rayleigh-Benard对流则是研究热对流现象的一个经典模型，是指在一个封闭的腔体内，其上表面温度恒定，下表面加热，从而形成温度差导致腔体内流体运动的流动现象。由于该系统试验简单且易于控制，以及描述该系统的精确方程已知，便于理论分析，故该模型已被普遍接受，是用来研究对流稳定性、时空结构和非线性特性的模型之一。

目前，对于Rayleigh-Benard对流问题研究手段主要有实验研究、模型方程探讨、流体力学方程数值模拟等方法[2-9]。王涛、葛永斌等人对腔体内的对流进行了高精度数值模拟,对双局部进行波的研究进一步进行了扩充，并研究了具有较弱Soret效应下，附加一个微小的温度扰动作为扰动源的中等长高比腔体内混合流体对流系统中时空结构的发展[10-12]。郝建武在长高比Γ=40、分离比ψ=-0.6的条件下，得到了一种新的现象，即单侧缺陷摆动对传行波，并对其形成机理与特性作了进一步探讨[13]。在弱非线性的假定下，在分歧点附近通过级数展开等方法，人们已建立了各种模型方程或振幅方程。这些方程包括：Ginzbarg-Landau(GL)方程式、复数GL方程式、耦合的GL方程式、Kuramoto-Sivashinsky方程式、Swift-Hohenberg方程式等[14-21]。

目前，基于对流振幅来表征行波对流斑图的研究报道还很少，本文利用Ginzbarg-Landau(GL)方程组，通过研究对流的振幅变化来探讨行波对流的斑图特性及非平衡体对流的非线性动力特性。

1 基本方程组

1.1 Ginzbarg-Landau(GL)方程组

本文研究行波对流的斑图时选取如下GL方程组[15-16]：

(1)

(2)

式中A、B为行波对流的振幅，τ0、ξ0、s分别反映对流运动的特性时间、长度、行进波的群速度；g1、g2、k反映非线性系数。

定义参数:

整理式(1)、(2),然后去掉方程(1)、(2)参数的“′”，则GL方程组可简化为：

(3)

(4)

方程(3)、(4)中，v反映行波群速度，ε反映相对瑞利数，g代表非线性系数。

两端采用反射边界条件,方程形式为[16]：

(5)

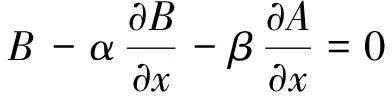
(6)

其中 ，α、β为反射系数，计算中取α=-0.06,β=-0.06。

本文在计算时给出左行波振幅A和右行波振幅B的初值分别为:

式中L代表腔体长度。

1.2 振幅方程组的差分式

GL方程组简化式经过一阶差分和二阶差分，式子为：

(7)

(8)

左边界方程的差分式为：

(9)

(10)

右边界方程的差分式为：

(11)

(12)

2 结果与分析

通过对有限腔体长度L=20、L=40、L=60内的对流进行模拟，分析了在不同腔体长度下，行波振幅随相对瑞利数和群速度的变化，发现了行波振幅存在三种状态：TI(Time independent),即行波的振幅不随时间变化；TD(Time dependent),即行波的振幅对时间有依赖性，随时间发生变化；Null,即行波的振幅为零。

将振幅状态与实际流体斑图状态一一对应，发现存在行波(Traveling wave(TW))、局部行波(Localized traveling wave (LTW))、对传波(Counterpropagating waves (CPW)) 、Blinking traveling wave(BTW)斑图。并在ε-v平面中根据行波对流振幅的变化情况进行了分区。

2.1 行波对流的斑图

2.1.1 振幅状态为TI的对传波CPW

对于在腔体总长度为60个单位长度，群速度v=1.0，相对瑞利数ε=0.29的情况，得到了振幅状态为TI的对传波CPW，如图1所示。通过对图1的分析，得到以下特性。

经过250个单位时间左右行波对流状态都达到稳定。在长度为60个单位长度的区间内，左行波从腔体的最左端即L=0处到L=20处附近振幅为0.5，然后在L=20处振幅开始衰减，到L=35附近处开始衰减为零，一直延续到L=50附近振幅仍为零，而后一直到腔体的右边壁L=60处行波振幅有小幅度的回升，其数量级是10-2级，大小可以忽略，在整个长度区间左行波保持这种状态不随时间变化而持续前进；右行波从腔体的最右端L=60处开始一直到L=45处附近行波振幅为0.5，随后振幅开始出现连续性衰减，直到L=30个单位长度附近振幅为零，这种状态一直延续发展到L=10处附近振幅仍为零，而后行波振幅出现“抬头”并保持增长直到腔体的最左端L=0处，其数量级也是10-2级，大小可以忽略，右行波在整个腔体长度区间内保持这种状态且不随时间发生变化而发展下去。

图1 L=60, v=1.0, ε=0.29左右行波振幅

左右行波的振幅状态达到稳定后都不随时间发生变化即振幅状态为TI状态，此种波在实际中对应对传波。

2.1.2 振幅状态为TD的BTW

腔体长度L=60、群速度v=1.5、相对瑞利数ε=0.2的振幅情况如图2所示。通过对图2的分析，得到以下特性。

左右行波的对流状态在达到稳定后，其振幅均表现出了“杂乱”性，且振幅大小随时间发生变化，即振幅状态都为TD。

左行波振幅在腔体的左端开始发展，在L=10处附近振幅达到最大值0.4，而后出现连续性衰减直到腔体的最右端为零，随着时间的发展，出现最大振幅区域的长度与整个腔体长度的比例时而变小，如250个单位时间到300个单位时间段；时而在整个腔体中振幅为零，如350个单位时间到390个单位时间段；时而变大，如425个单位时间到450个单位时间段。右行波也展现出了类似的特性。

此种波在实际中对应Blinking traveling wave(BTW)。

图2 L=60, v=1.5, ε=0.2左右行波振幅

2.1.3 振幅状态为Null的行波

腔体长度L=60、群速度v=1.0、相对瑞利数ε=0.0的振幅情况如图3所示。通过对图3的分析，得到以下特性。

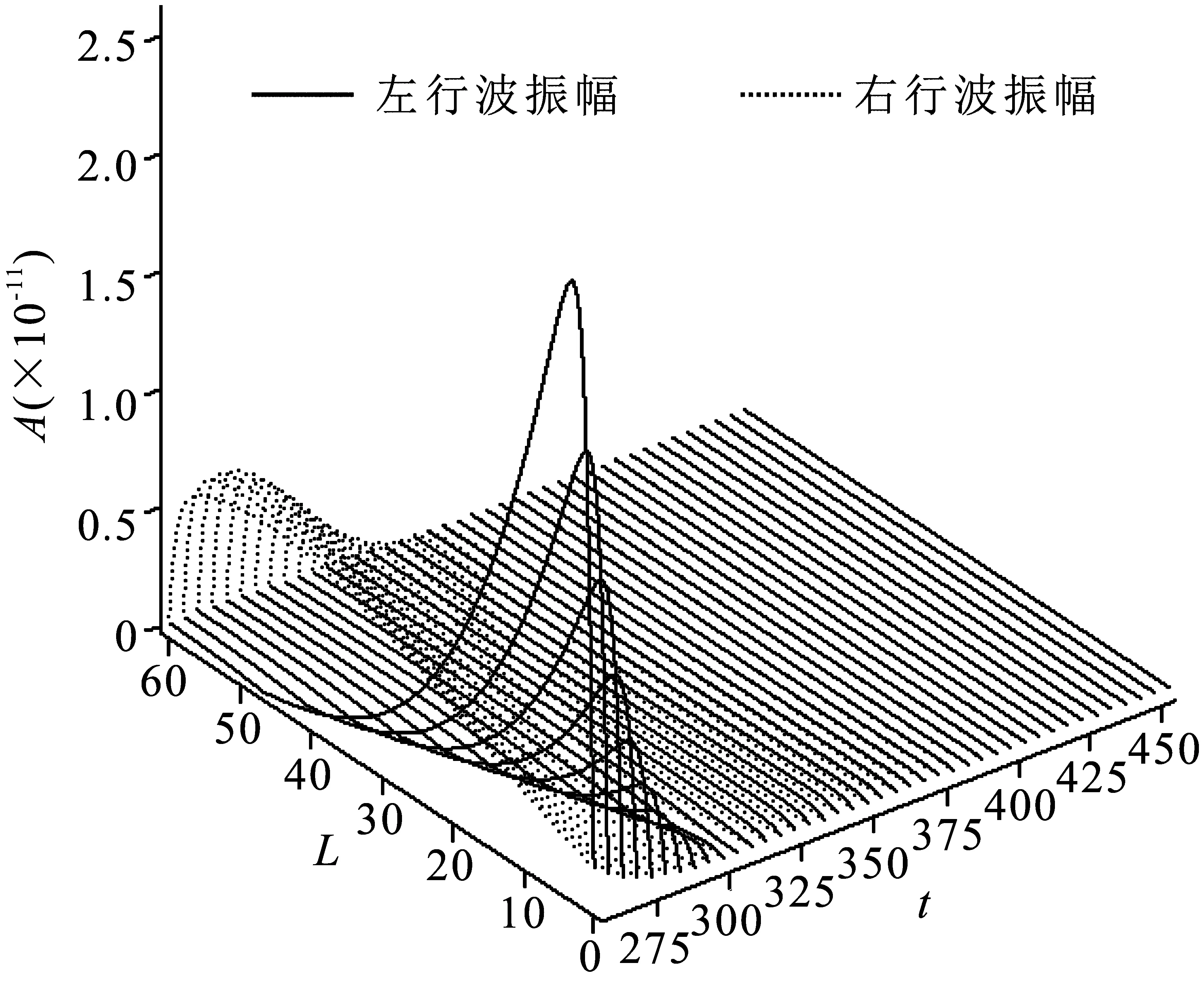
图3 L=60, v=1.0, ε=0.0左右行波振幅

经过300个单位时间对流达到稳定。

达到稳定状态后左行波与右行波振幅都为零，且都不随时间发生变化，即振幅状态为Null。

左右行波振幅都为零，且不随时间发生变化即振幅状态为TI。

2.1.4 振幅状态为TI的行波TW

腔体长度L=40、群速度v=0.2、相对瑞利数ε=0.6的振幅情况如图4所示。通过对图4的分析，得到以下特性。

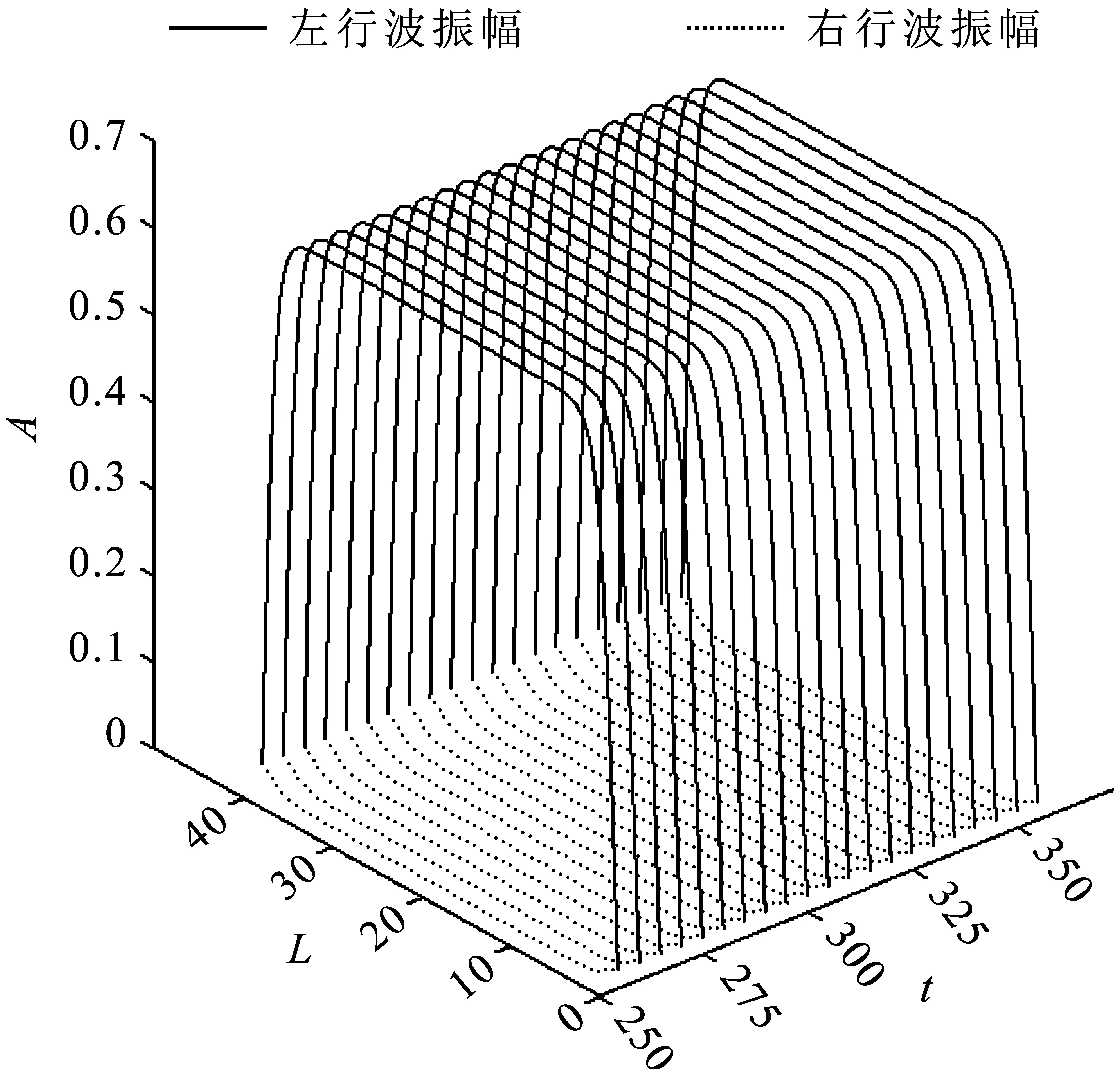
图4 L=40, v=0.2, ε=0.6左右行波振幅

经过250个单位时间，左右行波对流状态都达到稳定。

在长度为40个单位长度的区间内，左行波从腔体内部L=5处到L=35处附近振幅为零，但在腔体的两端L=0到L=5附近及L=35到L=40附近，振幅出现“抬头”并保持增长，其数量级是10-2级，大小可以忽略。

右行波在整个腔体内振幅大小恒为0.6，保持这种状态且不随时间发生变化地发展下去。

左右行波的振幅状态达到稳定后都不随时间发生变化即振幅状态为TI状态，此种波在实际中对应行波。

2.1.5 振幅状态为TD且具有一定周期性的行波

腔体长度L=40、群速度v=1.5、相对瑞利数ε=0.3的振幅情况如图5所示。通过对图5的分析，得到以下特性。

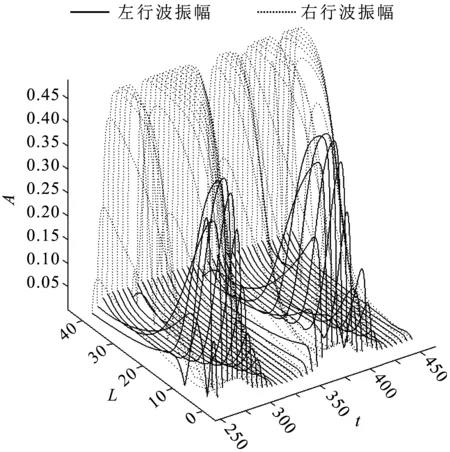
图5 L=40, v=1.5, ε=0.3左右行波振幅

左右行波振幅状态表现为TD，但区别于BTW，即出现了一定的周期性和对称性。左右行波的变化周期均为100个单位时间左右。

2.1.6 振幅状态为TI的局部行波LTW

腔体长度L=20、群速度v=0.5、相对瑞利数ε=0.2的振幅情况如图6所示。通过对图6的分析，得到以下特性。

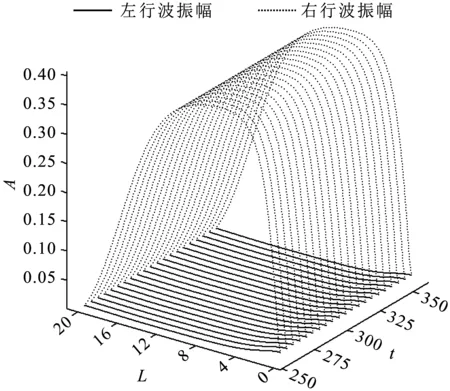
图6 L=20, v=0.5, ε=0.2左右行波振幅

右行波在腔体两端同时连续增长，最终在腔体中间L=4到L=12区域振幅保持最大值0.4;左行波振幅在整个腔体内一直为零，但在腔体的左端有轻微“抬头”，数值可以忽略。腔体中仅仅留下右行波。

左右行波振幅状态表现为TI状态，对应局部行波。

2.2 振幅状态分区图

2.2.1L=60的行波振幅状态分区

在长度L=60的腔体内，笔者研究了行波振幅随群速度v在0.0～2.0、相对瑞利数ε在-0.20～0.60的范围内的分区情况，如图7所示。

图7 L=60的行波振幅状态分区

群速度v=0时: 临界状态出现在相对瑞利数ε=-0.01处，此时当相对瑞利数ε再增大0.01即ε=0.00时行波振幅随时间的变化情况就发生明显变化：-0.20≤ε≤-0.01时，左右行波稳定后,行波振幅都变为零，即处于Null区域；0.00≤ε≤0.60时，左右行波稳定后, 左右行波振幅不随时间变化，即处于TI区域。同理，在v=0.25时临界点ε=0.00；在v=0.5时临界点ε=0.02。

群速度v=0.75：-0.20≤ε≤0.03时，行波振幅处于Null区域；0.14≤ε≤0.15时，处于TD区域；0.16≤ε≤0.60时，行波振幅处于TI区域。同理，在v=1.0时有两个临界点ε=0.04和ε=0.28；在v=1.25时有临界点ε=0.05和ε=0.42。

群速度v=1.5：-0.20≤ε≤0.05时，行波振幅处于Null区域；0.06≤ε≤0.60时，行波振幅处于TD区域。同理，在v=1.75时临界点是ε=0.07；在v=2.0时临界点是ε=0.07。

在群速度v=0.0到v=0.55，行波振幅状态划分为Null与TI两个区域; 在群速度v=0.55到v=2.0，行波振幅状态划分为Null、TD及TI三个区域。

2.2.2L=40的行波振幅状态分区

L=40的行波振幅分区图如图8所示。v=0、 -0.20≤ε≤ -0.02时，行波振幅处于Null区域；v=0，-0.01≤ε≤0.60时，行波振幅处于TI区域。同理，在v=0.25时临界点ε=0.01,在v=0.5时临界点ε=0.03。

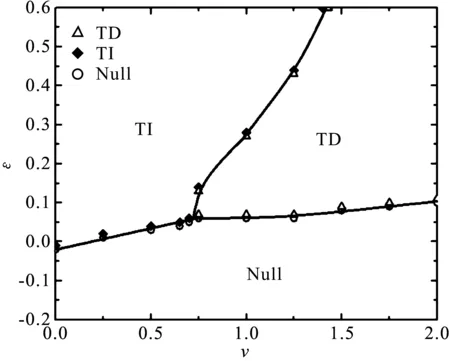
图8 L=40的行波振幅状态分区

群速度v=0.75：-0.20≤ε≤ 0.06时，行波振幅处于Null区域；0.07≤ε≤ 0.13时，即处于TD区域；0.14≤ε≤ 0.60时，行波振幅处于TI区域。同理，在v=1.0时有两个临界点ε=0.06和ε=0.27；在v=1.25时有临界点ε=0.06和ε=0.43。

群速度v=1.5：-0.20≤ε≤ 0.08时，行波振幅处于Null区域；0.09≤ε≤ 0.60时，行波振幅处于TD区域。同理，在v=1.75时临界点ε=0.09；在v=2.0时临界点ε=0.10。

在群速度v=0.0到v=0.75，行波振幅状态划分为Null与TI两个区域，在群速度v=0.75到v=2.0，行波振幅状态划分为Null、TD及TI三个区域。

2.2.3L=20的行波振幅状态分区

在长度L=20的腔体内，左右行波振幅的划分区域如图9所示。

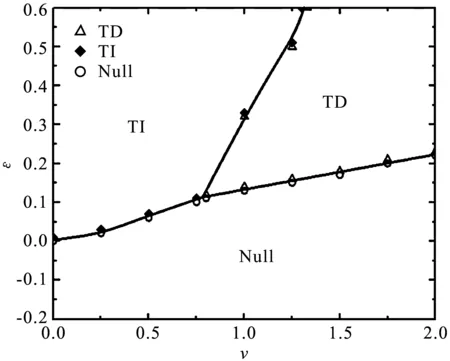
图9 L=20的行波振幅状态分区

群速度v=0：相对瑞利数-0.20≤ε≤ 0.00时，处于Null区域；0.01≤ε≤ 0.60时，处于TI区域。同理，在v=0.25时有临界点ε=0.02；在v=0.5时有临界点ε=0.06;v=0.75时有临界点ε=0.10。

群速度v=1.0：-0.20≤ε≤0.13时，行波振幅处于Null区域；0.14≤ε≤0.32时，处于TD区域；0.33≤ε≤0.60时，行波振幅处于TI区域。同理，在v=1.25时有临界点ε=0.15和ε=0.50。

群速度v=1.5：相对瑞利数-0.20≤ε≤0.17时，处于Null区域；0.18≤ε≤0.60时，行波振幅处于TD区域。同理，在v=1.75时临界点ε=0.20；在v=2.0时临界点ε=0.22。

在群速度v=0.0到v=0.8，行波振幅状态划分为Null与TI两个区域; 在群速度v=0.8到v=2.0，行波振幅状态划分为Null、TD及TI三个区域。

3 结 语

在腔体长度一定的情况下影响振幅状态的参数主要有两个：群速度与相对瑞利数。

随着群速度v与相对瑞利数ε变化，腔体长度L=20、L=40、L=60的振幅都被划分为“TI、TD、Null”三个区域，即时间独立区、时间依赖区、零振幅区。

在TI区，行波振幅不依赖于时间，即行波振幅达到稳定状态后不随时间而改变。它包括两种情况：①均匀行波，即左行波振幅稳定且不为零，右行波振幅稳定且为零，或者右行波振幅稳定且不为零，左行波振幅稳定且为零；②对传波，即左右行波振幅同时稳定存在且都不为零。

在TD区，行波振幅依赖于时间，即行波振幅达到稳定状态后随时间而变化，它包括两种情况：①BTW，即左右行波振幅都随时间在发生变化且杂乱无章；②空间周期性，即左右行波振幅随时间在发生变化但出现一定的对称性，具有周期性。

腔体长度L=20、L=40、L=60，在TI区域振幅都是经过了250个单位时间达到稳定；在Null区域振幅都是经过了300个时间单位达到稳定。

参考文献：

[1] 余荔，宁利中，魏炳乾,等. Rayleigh-Benard对流及其在工程中的应用[J]. 水资源与水工程学报，2008，19(3):52-54.

Yu Li, Ning Lizhong, Wei Binqian, et al. Rayleigh-Benard convection and application in engineering[J]. Journal o f Water Resources & Water Engineering, 2008，19(3):52-54.

[2] Ning Lizhong，Harada Y, Yahata H. Localized traveling waves in binary fluid convection[J]. Progress of Theoretical Physics,1996,96(4):669-682.

[3] Ning Lizhong, Harada Y, Yahata H. Dynamics of localized traveling wave in binary fluid mixtures [J]. Journal of Hydrodynamics, 1998,10(2):29-39.

[4] Ning Lizhong, Harada Y, Yahata H. Formation process of the traveling wave state with a defect in binary fluid convection [J]. Progress of Theoretical Physics，1997，98(3)：551-566.

[5] Ning Lizhong, Harada Y, Yahata H. Modulated traveling waves in binary fluid convection in an intermediate-aspect-ratio rectangular [J]. Progress of Theoretical Physics,1997,97(6)：831-848.

[6] 宁利中，余荔, 袁喆, 等. 沿混合流体对流分叉曲线上部分支行波斑图的演化[J].中国科学G，2009，39(5):746-751.

Ning Lizhong, Yu Li, Yuan Zhe, et al. Evolution of traveling wave patterns along upper branch of bifurcation diagram in binary fluid convection [J]. Science in China G, 2009,39(5): 746-751.

[7] 宁利中，齐昕, 周洋，等.混合流体行波对流中的缺陷结构[J].物理学报,2009，58(4):2528-2534.

Ning Lizhong, Qi Xin, Zhou Yang, et al. Defect structures of Rayleigh-Benard traveling wave convection in binary fluid mixtures [J]. Acta Phys Sin-cn ED, 2009,58(4):2528-2534.

[8] 赵秉新, 田振夫.底部加热平面Poiseuille 流中的局部行波结构[J].水动力学研究与进展：A 辑，2012,27(6):649-658.

Zhao Bingxin, Tian Zhenfu.Localized traveling wave convection in plan Poiseuille flow heated from below[J].Chinese Journal of Hydrodynamics, 2012,27(6):649-658.

[9] 齐昕，宁利中，刘嘉夫，等. 中等长高比腔体内的混合流体Undulation行进波[J].西安理工大学学报,2010,26(3):271-276.

Qi Xin,Ning Lizhong,Liu Jiafu,et al.Undulation travelling wave convection in binary fluid mixtures in an intermediate-aspect-ratio cell[J].Journal of Xi’an University of Technology,2010,26(3):271-276.

[10] 王涛，田振夫，葛永斌．长腔体内混合流体行进波对流的高精度数值模拟[J]．水动力学研究与进展：A 辑，2011,26(1):41-47.

Wang Tao,Tian Zhenfu,Ge Yongbin.High accuracy numerical simulation of travelling wave convection in binary fluid mixture in large aspect ratio rectangular cell[J].Chinese Journal of Hydrodynamics,2011,26(1):41-47.

[11] 王涛，葛永斌．双局部行进波对流的高精度数值模拟[J]．合肥工业大学学报：自然科学版，2012,35(6):842-847.

Wang Tao,Ge Yongbin.High accuracy numerical simulation of doubly localized travelling wave convection [J].Journal of Hefei University of Technology(Natural Science),2012,35(6):842-847.

[12] 王涛，葛永斌.微小扰动下中等长高比腔体内行进波对流的高精度数值模拟[J].合肥工业大学学报：自然科学版,2012,35(11):1569-1573.

Wang Tao,Ge Yongbin.High accuracy numerical simulation of travelling wave convection in an intermediate-aspect-ratio rectangular cell with small perturbation[J].Journal of Hefei University of Technology(Natural Science),2012,35(11):1569-1573.

[13] 郝建武，宁利中，王卓运，等．长进行截面腔体内具有缺陷的对传行波斑图[J]．力学季刊，2013，34(1)：139-146.

Hao Jianwu,Ning Lizhong,Wang Zhuoyun,et al.Patterns of counter propagating wave with defects in a long rectangular cell[J].Chinese Quarterly of Mechanics,2013，34(1)：139-146.

[14] Aranson I S，Kramer L. The world of the complex Ginzburg-Landau equation[J].Review of Modern Physics, 2002,74(1):99-143.

[15] Sullivan T S，Deissler R J. Elimination of hysteresis in a system of coupled Ginzburg-Landau equations [J]. Physical Review A,1989，40(11):6748-6751.

[16] Cross M C. Structure of nonlinear traveling-wave states in finite geometries[J].Physical Review A,1988，38(7):3593-3600.

[17] Cross M，Hohenberg P C．Pattern formation outside of equilibrium[J]. Reviews of Modern Physics，1993, 65 (3): 855-1112.

[18] RIECKE. Self-trapping of traveling-wave pulses in binary mixture convection[J]. Physical Review Letter,1992,(68):301-304.

[19] Cross M, Greenside H.Pattern formation and dynamics in nonequilibrium systems[M]. UK:Cambridge University Press,2009.

[20] 蔵本由記,川崎恭治,山田道夫,等.パターン形成[M]．東京：朝倉書店，1991：1-146．

[21] 森肇,蔵本由記.散逸構造とカオス[M]．東京：岩波書店，2000：1-46.