晶体在立方体晶格移动的最短路径问题研究
张娜,王家民,陈小军 , 窦忠发
(1.西安理工大学 机械与精密仪器工程学院,陕西 西安 710048; 2.陕西省地方电力(集团)有限公司,陕西 西安 710061; 3.中航工业618所,陕西 西安 710065)
很多场景都涉及晶体在立方体晶格中的移动问题。例如,现代物流业的立体仓库,立体仓库可以看成是一个立方体晶格,其中存放货物的货架相当于晶格中的晶体[1]。当满载货物的立体仓库中的各个货架上的物品需要调整时,通过货位移动,完成位置调整,这个过程可以抽象为晶体在立方体晶格中的移动。为了降低成本并提高工作效率,晶体在立方体晶格中的移动往往通过最短路径来实现[2]。
很多空间最小值问题经过数学模型转换,都可以转化成一个最短路径问题[3-7]。最短路径问题最初是为解决交通运输而提出的。随着我国国民经济的快速发展,除交通运输领域,物流仓储、工业生产等基础领域也出现了最短路径问题。最短路径问题与社会经济生活的联系越来越紧密。求解最短路径的算法主要有Dijkstra算法、A*算法、D*算法、Floyd-Warshall算法、Bellman-Ford算法、SPFA算法等[8-16]。
晶体在晶格中移动的最短路径求解实际上是一个多源多路径的动态环境问题,改进型的D*算法和Floyd-Warshall算法可以求解,但这两种算法设计较为复杂,且效率不高[17-19]。本文在求解晶体在晶格中移动时,将晶格抽象成魔方结构,通过模型转换,将魔方结构变成一个包含多个移动体的拓扑结构图,该最短路径问题可转化为典型最短路径算法来解决,算法在单路径寻找时以Dijkstra算法为基础,加入当前最佳移动晶体的选择功能及晶格结构变化调整的操作,来完成最短多源多路径选择。该算法的贡献在于通过对每次移动步数最小的晶体挑选和对晶格状态的动态更新,使全体晶体从初始状态逼向最终状态为总体步数最小。
1 晶体在晶格中移动图模型的构建
1.1 晶体移动的规则
晶体在晶格中移动模型可以用图1所示的魔方结构来描述,利用各类颜色代表不同元素方位的类别,晶体在晶格中移动的过程就是使不同颜色的单元都归在魔方的6个方向的过程。

图1 基于魔方结构的晶格
与魔方结构单元的运动方式不同的是,魔方结构的单元只能在单面将所有单元整体移动,而在晶格模型中,只要所有路经的晶格不存在障碍晶格,每个晶体都可以在晶格中向其他相邻晶格自由移动。由于障碍晶格直接影响了路径选择,而晶格中的每个晶体在移动过程中又会对其他晶体的移动产生影响,故每个移动晶体的起点和终点均互相交叉,晶格所走的路径将是动态变化的,而不是固定存在的路径。由此可见,求晶体在晶格中移动的最短路径问题必须进行模型转换,将动态的路径选择转化为相对静止的路径选择,将多源晶体的移动转为多个单一晶体的相对移动。
1.2 晶体移动的图模型
从图拓扑结构的角度看,晶格的信息可以转化为顶点的信息和描述顶点之间关系的信息。将晶格中的每个晶体所在的位置理解为拓扑图结构中的一个顶点,晶体所在的位置与周围晶体所在位置的移动关系理解为顶点之间连接关系的信息。当相邻晶体位置不存在障碍晶格时,每个晶体与周围的晶体存在连接关系,而当存在障碍晶格时,则不存在连接关系。由此,在多个晶格都处于运动时,每个晶体与周围的晶体的连接关系是动态的。当晶体在图结构上运动后,需要立即更新顶点之间关系的信息。
典型的最短路径算法,主要用于计算一个节点到其他所有节点的最短路径,以起始点为中心向外层层扩展,直到扩展到终点为止。与单一物体在图结构上从起点经过连续路径到终点的移动轨迹不同,晶格中所有的晶体都需要经过从起点到终点的路径,每次移动的可以是当前任何一个不存在任何障碍的晶体。由此可知,最短路径算法不仅仅要考虑选择当前晶体走哪条路径,而且要考虑先走哪个晶体的问题。构造的模型如图2所示。
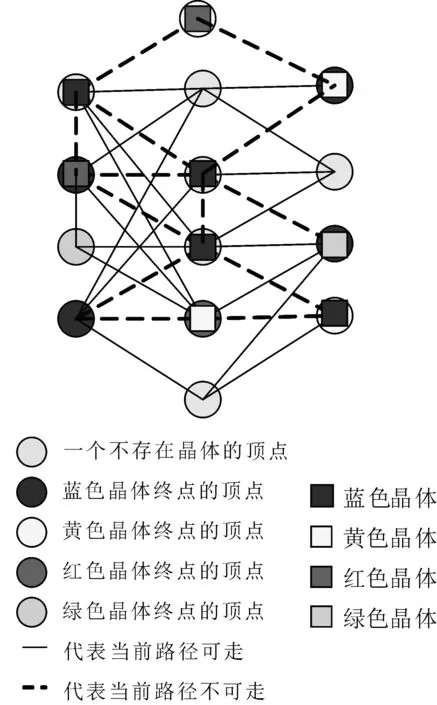
图2 晶格的网络拓扑图
图2的模型用不同的颜色代表不同的晶体类型,所有晶体最终要运动到颜色一致的顶点,例如,“”晶体最终要到达“”顶点,其它颜色的晶体类似。
2 算法设计
2.1 数据结构
对于一个有M个晶体、N个位置的晶格,对其数据结构描述如下。
1) 晶格六面体的方向描述。可将六面体的元素方位分为Us[6]={U1,U2,U3,U4,U5,U6}。每个方位都可以用图2模型中的不同颜色来表示。
2) 顶点的描述。顶点是一个数组Vs[N]={V1,V2,…,VN},其中的元素Vi具有属性U,代表所属方位,Vi·U∈{U1,U2,U3,U4,U5,U6},即顶点数组中的元素都可以归类到其中一个方位。
3) 边之间关系描述。任意两个顶点之间存在路径即为边,边之间的关系实际上是一个N×(N-1)的二维矩阵的计算机存储表示问题,边是一个二维数组Cs[N][N-1]={{V1,V2},{V1,V3},… ,{VN,VN-1}}。二维数组Cs[N][N-1]的取值分二种情况:①由于每个顶点只可能和周围的最多6个顶点成为邻接顶点,当某顶点与另一顶点不是邻接顶点时,Cs[N][N-1]的取值为0;②当某顶点与另一顶点是邻接顶点,且二者当前的连接关系为“—”时,Cs[N][N-1]的取值为1;二者当前的连接关系为“- -”时,Cs[N][N-1]的取值为0。
4) 晶体描述。晶体集合是一个数组S[M]={S1,S2,…,SM},其中的元素Si具有属性U,代表所属方位,取值为Si·U∈{U1,U2,U3,U4,U5,U6},即晶体集合数组中的元素都可以归类到其中一个方位。
5) 晶体位置状态描述。令晶体位置是一个二维数组L[M][M],其元素为
6) 当前位置到源点路径的描述。晶格中每个晶体都要完成从起始顶点到终止顶点的运动路径,对于一个具有M个晶体(M 7) 晶体在晶格中的移动路径描述:晶体在晶格中移动的路径集合是一个数组pathNodes[],数组中的元素为 在此提出一种晶体在晶格中移动的最短路径算法(CMCLA),其伪代码描述如图3所示。 图3 CMCLA算法描述 CMCLA算法的基本思想为: 设置顶点集合prev[M][maxnum]并不断地作贪心选择来扩充这个集合,最终求出最短路径。其中,当前晶体集合S[M]的每一个晶体都要完成从起始位置状态到晶体终止位置状态的路径移动。 例如在晶体S[1]的路径移动中,一个顶点属于集合prev[1][j],当且仅当从源到该顶点的最短路径长度已知。初始时,prev[1][j]中仅含有S[1]所在的起始位置状态。设v是晶格中的某一个顶点,把从起始顶点到v且中间只经过prev[1][j]中顶点的路径称为从源到d的特殊路径,并用数组dist[i][j]记录当前每个顶点所对应的最短特殊路径长度。每次从V-prev[1][j]中取出具有最短特殊路径长度的顶点v,将v添加到prev[1][j]中,同时对数组dist[1][j]作必要的修改。该过程持续进行直到满足全局条件:当且仅当所有的晶体元素都有Si·U=Vi·U。其他晶体的移动与S[1]的移动的处理完全一致。 CMCLA算法通过每次移动步数最小的晶体挑选和晶格状态的动态更新,使全体晶体从初始状态逼向最终状态。对于一个M个晶体、N个位置的晶格,令d为采用d路堆实现优先队列ADT,函数SelectCurrentCrystal的复杂度为(M*N)2,searchPath的时间复杂度为M*lgN,computeShortestPath的时间复杂度为M*N,主函数的时间复杂度为N*M,在最坏的条件下CMCLA算法的时间复杂度是O(N3M4*lgN* lgd(M))。CMCLA算法中变量prev[M][maxnum]、dist[M][maxnum]、Cs[N][N-1]使用的空间最大为O(N*N),其他局部变量使用的空间O(M*N),由此CMCLA算法的空间复杂度是O(N2)。 CMCLA算法通过每次对移动步数最小的晶体的挑选和对晶格状态的动态更新,使全体晶体从初始状态逼向最终状态。算法中有以下两点与典型的最短路径算法不一样。 1)M个晶体的同时移动,每个时刻只能选择一个晶体移动,处理时首先挑选S[M]中可移动的晶体进入集合s[m],然后从prev[M] [maxnum]中选择s[m]中移动步数最少的晶体命名为currentCrystal,作为当前移动的晶体。 2) 每次从V-prev[i][j]中取出具有最短路径长度的顶点u后,将u添加到prev[i][j]中,在对数组dist[i][j]作必要修改的同时,更新晶体位置状态L[M][M]和边之间的关系Cs[N][N-1](即当相关顶点当前的连接关系为“—”时,Cs[N][N-1]的取值为1;相关顶点当前的连接关系为“- -”时,Cs[N][N-1]的取值为0)。 通过仿真实验验证晶体在晶格中移动的最短路径算法(CMCLA)。基于图1所示魔方结构,在进行模型转换后,利用C语言实现上述算法。实验数据分成两组。 1) 第一组:采用立方体晶格边分别为4(顶点数为64)、5(顶点数为125)、6(顶点数为216)和7(顶点数为343)的四种晶格为基础,晶体的数量为18(最终状态是六面体的每个方位都有3个晶体),起始状态为晶体在其晶格六面体每个方位的反面。 2) 第二组:以边为7(顶点数为343)的晶格为基础,晶体的数量分别为18(最终状态是六面体的每个方位都有3个晶体)、24(最终状态是六面体的每个方位都有4个晶体)、30(最终状态是六面体的每个方位都有5个晶体)、36(最终状态是六面体的每个方位都有6个晶体)四种情况,起始状态为晶体在其晶格六面体每个方位的反面。 算法在2.8 GHZ Intel core2 CPU、带有PAE的2G内存和160G硬盘的PC机上运行,经过运行,所有设定的晶格都从初始状态到达了最终状态,算法的运行结果如图4和图5所示。 图4 最短路径与立方体晶格顶点数量之间的关系 图5 最短路径与晶体数量之间的关系 图4是晶体数量为18时,四组输入数据状态下的最短路径与立方体晶格顶点数量之间的关系。图5是立方体晶格顶点数量是343时,四组输入数据状态下的最短路径与晶体数量之间的关系。从图4可以看出,随着立方体晶格顶点数量的增加,最短路径的长度也增加,二者增长幅度大致相同。从图5可以看出,随着晶体数量的增加,最短路径的长度也是增加的,但二者的增长幅度不一致,晶体数量增加的曲线较为平缓,但最短路径的长度呈快速增长的趋势。 对第二组运行数据,进一步分析晶格顶点数量是343时的四组数据中的晶体运行轨迹。四组数据从起点到终点的变化中,已完成晶体数量与移动步数之间的关系如图6所示。 图6 完成晶体数量与移动步数之间的关系 由图6可以看出,对于四组输入,算法总的趋势是随着时间进度的推移,完成晶体数量从0逐渐逼近了最终状态,分别是312步完成18个晶体移动,456步完成24个晶体移动,634步完成30个晶体移动,789步完成36个晶体移动。但该过程不成线性关系,而是接近负指数函数关系,即前述少量时间完成了大部分晶体的移动,而后续大部分时间均用在少数晶体的移动。这是因为算法在后续存在路径迂回现象。算法未加入启发式规则,使得位置查找过程存在重复。这也说明了算法还有很大的改进余地。 CMCLA是一个在动态环境中解决多源多路径问题的最短路径算法,在本文相关工作中列出的最短路径算法中D-Star和Floyd-Warshall算法也可以解决此类多源多路径问题。采用C语言实现D-Star和Floyd-Warshall算法,并将这两种算法及CMCLA算法以下列输入数据在同样的硬件机器上分别运行4次后,记录每次的运行时间,然后取平均值,其运行完成时间的如图7和8所示。 图7表明,在晶体相同的条件下,对于CMCLA、D-Star和Floyd-Warshall三种算法,随着晶格数据的增加,运行时间均呈现增加的趋势,而且晶格越多,增长的幅度越大。在晶体数量相同条件下,三种算法除了在晶格顶点数量为64时,D-Star运行时间最短(这是因为D-Star算法在晶格数量比较少时,启发式搜索使得收敛速度快),在其他状态下,CMCLA算法的运行时间均比D-Star和Floyd-Warshall短。这说明晶格数量较少时,CMCLA算法与D-Star算法相比无优势,而当晶格数量较多时,CMCLA算法具有明显的优势。 图7 晶体相同、晶格不同条件下的运行时间比较 图8 晶体不同、晶格相同条件下的运行时间比较 从图8可看出,在晶格相同的条件下,对于CMCLA、D-Star和Floyd-Warshall三种算法,随着晶体数据的增加,运行时间均呈现增加的趋势。三种算法中,在四种状态下,CMCLA运行时间均比D-Star和Floyd-Warshall短。 从上述实验可以看出,当晶体和晶格数量较少时,CMCLA无法体现出在运行时间上的优势,而当晶格的规模达到较大数量时,特别是晶体数量也较多时,CMCLA的运行效率将充分体现出来。这证明,在大规模晶体晶格结构中,CMCLA算法能实现利用最低成本完成移动,提高工作效率、节约时间,具有重要的应用意义。 从空间复杂度方面分析,CMCLA算法由于是在立方体模型的基础上实现的,并且算法设计思路是寻求立方体中多源多路径的最短路径,而D-Star和Floyd-Warshall算法主要针对平面图查找最短路径,因此,CMCLA算法空间复杂度要大于D-Star和Floyd-Warshall算法空间复杂度。 从时间复杂度方面分析,由于在魔方结构的立方体晶格中需要进行多源多路径的最短路径查找,使得D-Star和Floyd-Warshall实现时,算法设计较为复杂,运行次数和运行时间受到多源多路径因素和算法设计自身的影响,造成算法时间复杂度的增加。而CMCLA算法自身考虑到晶体结构,将魔方结构变成一个包含多个移动体的拓扑结构图,通过对每次移动步数最小的晶体的挑选和路径晶格状态的动态更新,使全体晶体以总体步数最小从初始状态逼向最终状态,从而节约了算法的执行时间。因此,当立方体晶格数量较少时,多源多路因素对三种算法的影响较小,三者的执行时间较为接近。而当立方体晶格数量较大时,CMCLA算法的时间复杂度相对于D-Star和Floyd-Warshall算法的时间复杂度越来越小。 寻找立方体晶格中晶体移动的最短路径与典型的最短路径有重要区别,但通过模型转换,它就变成了一个包括多个约束条件的典型最短路径问题。本文在模型构建的基础上,分析并提出了基于魔方的立方体晶格中晶体移动的最短路径算法CMCLA,算法的创新在于通过对每次移动步数最小的晶体挑选和对晶格状态的动态更新,使全体晶体以总体步数最小从初始状态逼向最终状态。实验结果表明,算法能有效解决晶体在立方体晶格中的移动问题,能以最低成本完成移动,提高工作效率、节约时间。 在未来的工作中,笔者将致力于以下三个方面的工作:①优化现有算法,减少算法的空间复杂度;②引入智能计算思想和启发式规则,使算法在挑选当前需移动的晶体和查找当前要移动到的位置时依据规则,有目标地缩小挑选和查找范围,提高算法的效率;③将现有算法进行扩展和延伸,以解决多维数据的最短路径查找问题。 参考文献: [1] 卢香清,李洪安,康宝生,等.图最短路径并行化及其应用研究[J].计算机工程与应用,2012,48(14):38-43. Lu Xiangqing,Li Hongan,Kang Baosheng,et al. Research on parallelization of shortest path for graph and its application[J].Computer Engineering and Applications,2012,48(14):38-43. [2] 杨帆,杨晓光,云美萍.考虑信号交叉口等待时间的最短路径算法[J].同济大学学报:自然科学版,2013,41(5):680-686. Yang Fan,Yang Xiaoguang,Yun Meiping.Shortest path algorithm with a consideration of waiting time at signalized intersections[J]. Journal of Tongji University(Natural Science),2013,41(5):680-686. [3] 王红梅,胡明.基于直接/间接邻边概念的最短路径算法[J].计算机应用,2010,30(5):1297-1299,1303. Wang Hongmei,Hu Ming. Shortest-path algorithm based on direct/indirect adjacent edge concept[J].Journal of Computer Applications,2010,30(5):1297-1299,1303. [4] 王树西,吴政学.改进的Dijkstra最短路径算法及其应用研究[J].计算机科学,2012,39(5):223-228. Wang Shuxi,Wu Zhengxue. Improved dijkstra shortest path algorithm and its application[J].Computer Science,2012,39(5):223-228. [5] Thouti, Krishnahari, Sathe S R.Performance analysis of single source shortest path algorithm over multiple GPUs in a network of workstations using open CL and MPI[J].International Journal of Computer Applications, 2013, 9(77): 31-36. [6] Jasika N, Alspahic N, Elma A, et al.Dijkstra’s shortest path algorithm serial and parallel execution performance analysis[C]//Proceedings of the 35th International Convention, MIPRO, 2012:1811-1815. [7] Huang Yizhen, Yi Qingming, Shi Min.An improved dijkstra shortest path algorithm[C]//Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering(ICCSEE 2013), 2013:26-29. [8] 刘明周,赵志彪,凌先姣,等.基于最短路径的复杂机械产品装配过程质量控制点公差带在线优化方法[J]. 机械工程学报,2012,48(10):173-177. Liu Mingzhou,Zhao Zhibiao,Ling Xianjiao,et al. Research on online tolerance optimization for complex mechanical products assembly process based on shortest path[J].Chinese Journal of Mechanical Engineering, 2012,48(10):173-177. [9] 徐涛,郑英,周念.物流最短路径规划最优化计算方法研究[J].物流技术,2013,32(7):236-238,262. Xu Tao,Zheng Ying,Zhou Nian. Study on optimal computation method of shortest logistics route[J]. Logistics Technology,2013,32(7):236-238,262. [10] Guerrero W J,Velasco N,Prodhon C,et al. On the generalized elementary shortest path problem: a heuristic approach[J]. Electronic Notes in Discrete Mathematics,2013,41(5):503-510. [11] Alireza Nazemi,Farahnaz Omidi. An efficient dynamic model for solving the shortest path problem[J]. Transportation Research Part C:Emerging Technologies,2013,26:1-19. [12] Keyur Rana, Mukesh Zaveri.A-star algorithm for energy efficient rounting in wireless sensor network[J].Trends in Network and Communications, 2011, 197: 232-241. [13] Fangfang T, Shiying Y, Xiaofeng Z, et al. Research on two-tiered A-star algorithm in game path-finding [J]. Microcomputer Applications, 2010, 1: 011. [14] Yao Junfeng, Lin Chao, Xie Xiaobiao, et al.Path planning for virtual human motion using improved A* star algorithm[C]//2010 Seventh International Conference on Information Technology: New Generations (ITNG), 2010:12-14. [15] Deng Yong,Chen Yuxin,Zhang Yajuan, et al. Fuzzy dijkstra algorithm for shortest path problem under uncertain environment[J]. Applied Soft Computing,2012,12(3): 1231-1237. [16] 武苏里,王湘桃,张阳,等.易阵游戏中两子交换算法的研究[J].计算机应用与软件,2009,26(2):272-274. Wu Suli,Wang Xiangtao,Zhang Yang,et al. On two-piece exchange algorithm in Yizhen game[J].Computer Applications and Software,2009,26(2):272-274. [17] Garg H, Rawat P. An improved algorithm for finding all pair shortest path[J]. International Journal of Computer Applications, 2012, 47(25):35-37. [18] 任小康,吴尚智,苟平章.基于动态状态树的回溯算法[J].计算机工程与设计,2007,28(4):755-756,759. Ren Xiaokang, Wu Shangzhi, Gou Pingzhang . Backtracking algorithm of dynamic state space tree[J].Computer Engineering and Design,2007,28(4):755-756,759. [19] 杨勇虎,李楠.平面魔方游戏中算法的设计和优化[J].计算机应用与软件,2010,27(8):273-275. Yang Yonghu,Li Nan. Designing and optimising algorithm for plane magic cube game[J].Computer Applications and Software,2010,27(8):273-275.2.2 算法描述

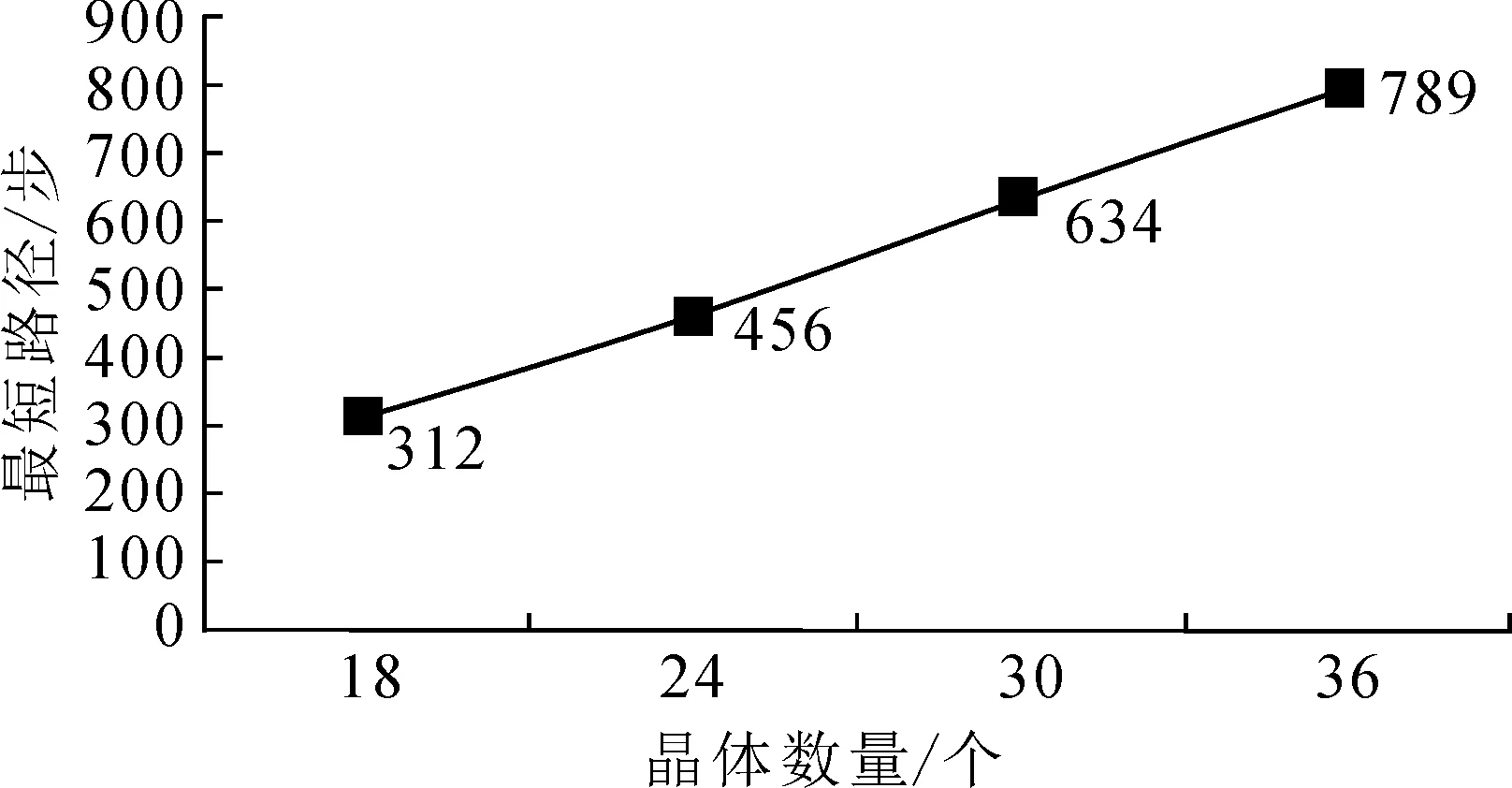
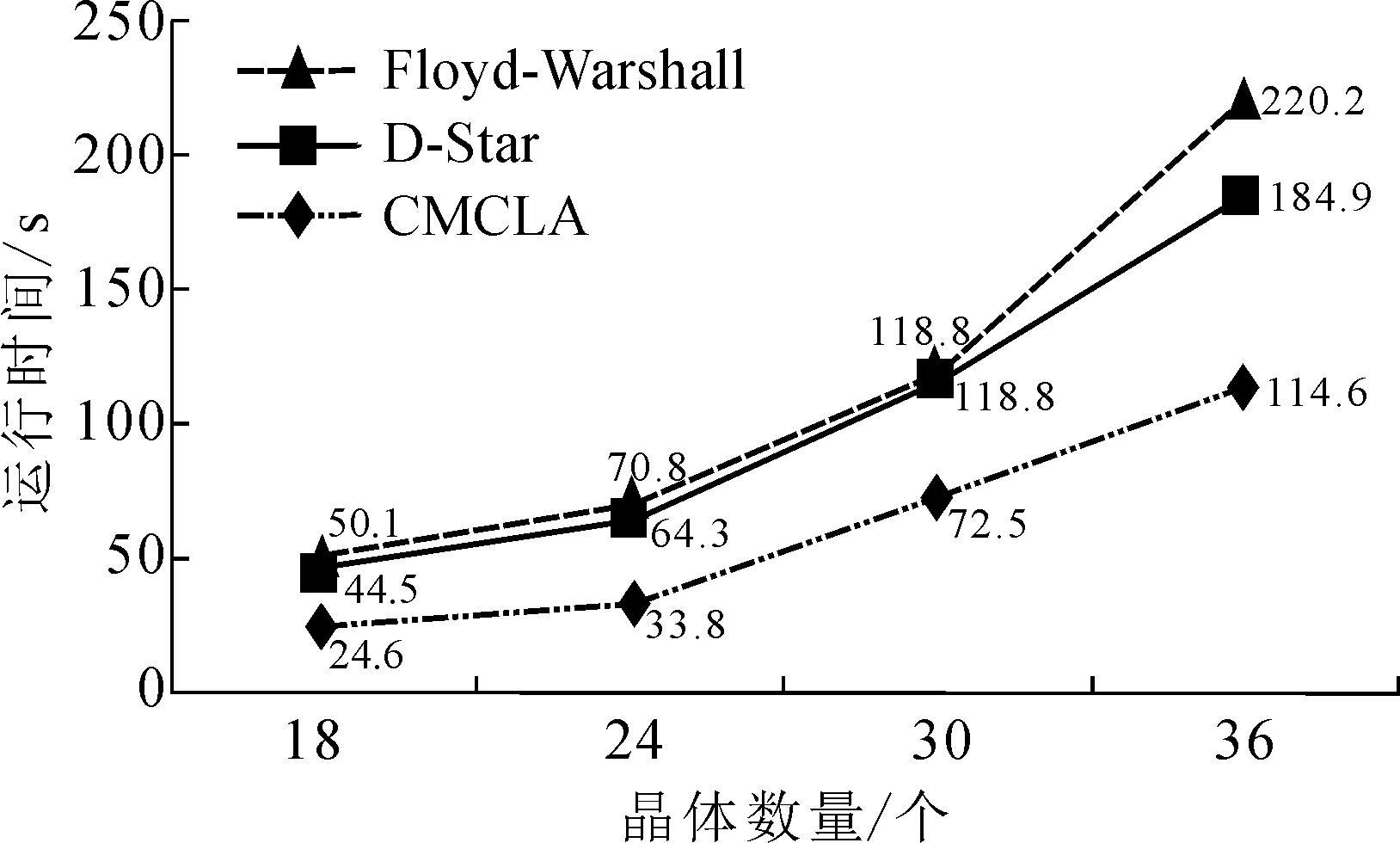
3 实验研究



4 结 语

