拉普拉斯特征向量相关谱及其在滚动轴承故障诊断中的应用

欧 璐， 于德介， 王翠亭

(湖南大学汽车车身先进设计制造国家重点实验室， 湖南 长沙 410082)

引 言

机械设备故障诊断的本质是根据设备运行状态信息进行特征提取和模式识别[1]。在旋转机械的故障中，有30%的故障是由滚动轴承引起的，滚动轴承工作状态的好坏将直接影响到整台机械设备的工作状态，因此轴承故障诊断技术已得到广泛的重视[2]。随着设备的日益复杂，反映设备状态的信息量越来越大，数据维数也越来越高，从而导致一些故障诊断方法(如模糊逻辑[3]，神经网络[4]，支持向量机等[5,6])的效率迅速下降。研究如何有效地从状态监测数据中提取故障特征，对提高故障监测与诊断的准确性具有重要意义。

谱方法是数学领域里一种经典的分析和代数方法,其在高维数据的低维表示和聚类问题中有着广泛的应用[7,8]。该方法首先根据给定的样本数据集定义一个描述成对数据点相似度的关系矩阵，并计算此矩阵的特征值和特征向量；然后选择合适的特征向量，投影得到数据的低维嵌入。如果相似度矩阵定义在一个给定的图上，比如图上的邻接矩阵、拉普拉斯(Laplacian)矩阵等，则称为谱图方法。近年来，随着谱图方法在流形学习中的深入研究，其应用也越来越广。JIANG等提出了一种新的监督流形学习算法——监督拉普拉斯特征映射(Supervised Laplacian Eigenmap，S-LapEig)，用于提取高维故障数据中的内在流形特征[9]。与传统的降维方法主元分析(Principal component analysis，PCA)、线性判别分析 (Linear discriminant analysis，LDA)和Laplacian特征图算法相比，S-LapEig能大大提高分类性能。YU等采用局部保持映射算法提取有效的特征集，进而分别采用多变量统计量和基于高斯混合模型的轴承性能退化评估模型来评估轴承的性能退化，都取得了很好的效果[10,11]。谱图方法的特征提取和维数简约能力在机械故障诊断领域有了一些应用，但在数据故障模式直接分类识别上的应用尚未见研究。

拉普拉斯特征向量相关谱定义为拉普拉斯矩阵特征向量之间夹角余弦的绝对值，通过对拉普拉斯矩阵进行标准正交分解得到，其表示形式是一种对称矩阵，能清晰反映数据在全局范围内的相互关系。由于不同类别故障样本在特征空间的投影方向不同，所以可以用拉普拉斯特征向量相关谱来进行滚动轴承故障的模式识别。本文提出了基于拉普拉斯特征向量相关谱的模式识别方法，并将其应用于滚动轴承故障诊断。应用实例表明，基于拉普拉斯特征向量相关谱可以有效地识别滚动轴承故障，是一种有效可行的滚动轴承故障诊断方法。

1 拉普拉斯特征向量相关谱

1.1 谱图方法简介

谱图方法主要通过图的各种矩阵表示(主要是拉普拉斯矩阵和邻接矩阵)来研究矩阵的谱性质(如特征值和特征向量)，从而刻画图中包含的信息，并通过几何、分析和代数的技术在离散空间和连续空间之间建立联系[12,13]。

设G=(V，E)是有n个顶点的简单图(不含环和重边)，其中V=(v1，v2，…，vn)表示顶点集合，E=(el，e2，…，em)表示边集合。图G的邻接矩阵定义为一个n×n矩阵A(G)=(aij)，其中当vi和vj相邻时aij=1；当vi和vj不相邻时aij=0。令d(vi)表示顶点vi的度，图G的拉普拉斯矩阵定义为

L(G)=D(G)-A(G)

(1)

式中D(G)=diag(d(v1)，d(v2)，…，d(vn))是图G的度对角矩阵。

拉普拉斯矩是建立在邻接矩阵的基础上，具有邻接矩阵不包含的顶点度信息，能更好地反映图中蕴含在顶点之间的关系。

1.2 拉普拉斯特征向量相关谱

本文在谱图理论的基础上，提出了拉普拉斯特征向量相关谱，定义为拉普拉斯矩阵特征向量间夹角余弦的绝对值。由拉普拉斯特征向量相关谱可构建对称的拉普拉斯特征向量相关谱矩阵，具体计算方法如下：

(1)用已知标号类别和未知标号类别的样本点构建一个近邻图G。总共m个样本点，其中，第i个节点对应样本xi。如果xi与xj足够近，则有边连接，例如，xi是xj的k近邻节点或者xj是xi的k近邻节点，否则，没有边连接；本文取k=m/2。

(2)如果节点i与节点j是连通的，即有边连接，则令(i,j=1,2,…,m)

Sij=exp(-d(xi,xj)2/2σ2)=exp(-d(xi,xj)2/t)

(2)

式中d(xi,xj)为样本xi与xj之间的欧式距离，σ为一个合适的常数，表示热核的宽度，在本文中令

式中t表示所有样本点之间的平均欧式距离；否则，没有边连接，Sij=0。加权矩阵S称为图G的相似矩阵，它用来衡量近邻样本点之间的相似性，描述了数据空间的固有局部几何结构；S中元素的值越大，表明两个样本越相近，越有可能属于同一类，反之，则越有可能属于不同类。

(3)定义单位向量

I=[1,…,1]T

(5)

对角矩阵

D=diag(SI)

(6)

则得到拉普拉斯矩阵矩阵[9]

L=D-S

(7)

其中I为m维单位向量。

(4)对半正定矩阵L求解其特征方程

|L-λI|=0

(8)

根据特征向量的定义(i,j=1,2, …,m)

Lφi=λiφi

(9)

令对角矩阵

γ=diag(λ1,λ2,…,λm)

(10)

正交矩阵

φ=[φ1,φ2,…,φm]

(11)

则可以得到

L=φγφT

(12)

(5)令由特征向量组成的单位正交矩阵

(13)

则将拉普拉斯矩阵标准正交分解为

L=ηTη

(14)

(6)拉普拉斯特征向量相关谱矩阵R第i行j列的元素R(ij)定义为(i,j=1,2,…,m)

(15)

式中ηki为单位正交矩阵的第i个特征向量的第k个元素；R(ij)为第i个样本与第j个样本的相关谱值，其物理意义为第i个样本与第j个样本在特征空间的夹角余弦的绝对值，用以衡量这两个样本间的相似程度。

(7)由于同类样本间的相关谱值远远大于不同类样本间的相关谱值，因此在相关谱矩阵R中定义一个阈值ε，对其进行处理得到优化后的相关谱矩阵R′

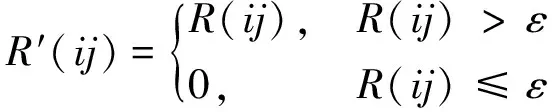
(16)

R′(ij)不为零表示第i个样本与第j个样本属于同一类，为零则表示第i个样本与第j个样本不属于同一类。由于相关谱矩阵是对称矩阵且只有有限种状态，因此根据同一行或者同一列的非0元素属于同一类的判别准则，观察矩阵的前若干行或者列就可以识别故障类别。

矩阵的构建和分解在谱图理论中起着很重要的作用，相关谱的表达形式也是一种矩阵，它通过标准正交分解拉普拉斯矩阵得到的特征向量来描叙样本间的相互关系。该方法无需对特征集进行筛选，分类精确度高，并且适用于小样本实验；同时，它将分类问题转化为求特征值问题，不需要迭代计算，具有计算过程简单、运算速度快等特点。相比神经网络而言，该方法不会依赖于使用者的经验知识，不存在考虑网络的稳定性以及泛化能力的问题；相比二分类的支持向量机而言，该方法可以进行多类故障分析，不需要考虑核函数及其参数调整对结果的影响。

由于不同类别故障样本在特征空间的投影方向不同，所以可以通过分析特征向量相关谱矩阵来进行滚动轴承故障的模式识别。

2 故障诊断原理

由以上分析可知，拉普拉斯特征向量相关谱可以对滚动轴承状态进行分类，进而诊断滚动轴承故障，其故障诊断流程见图1所示，该流程主要包括特征提取和模式识别两部分。

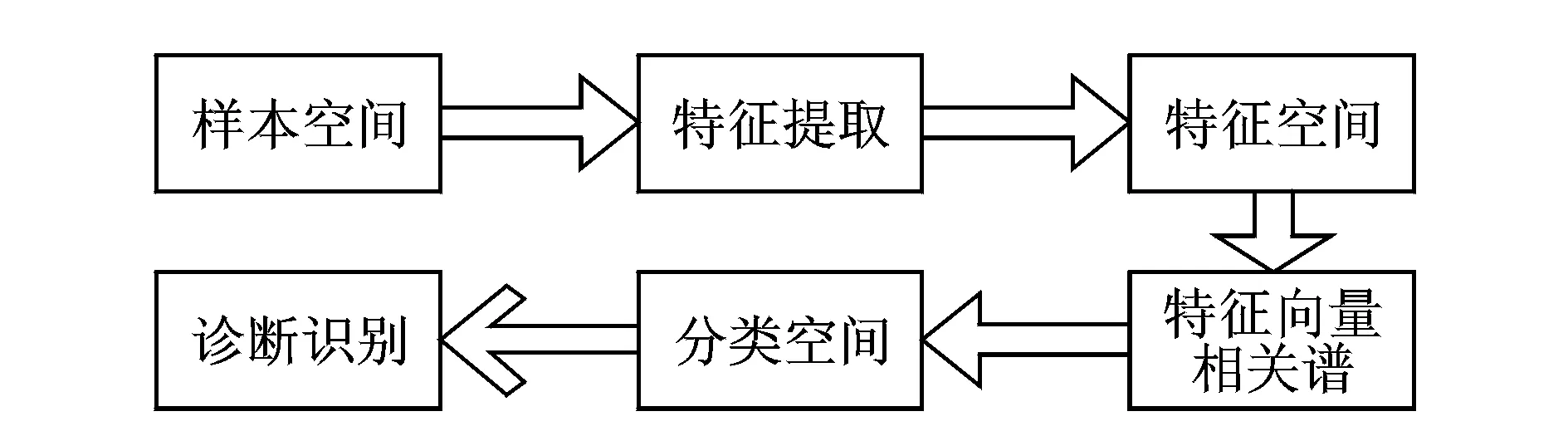
图1 故障诊断流程图

2.1 特征提取

当设备出现故障时，时域信号的幅值和概率分布将会发生变化；信号中的频率成分、不同频谱的谱峰位置也将发生变化。因此，通过描述信号时域波形和频域波形分布等特征，可以反映振动信号的时域和频域信息，从而指示故障的出现。为了获取更多的故障信息，用经验模态分解(Empirical mode decomposition，EMD) 方法对每个信号进行分解得到前若干个内敛模态分量(Intrinsic mode function，IMF)，然后分别计算每个IMF的能量熵[14]。其能量熵的定义为

(16)

式中pi为第i个IMF的能量占整个信号能量的百分比(i=1,2,…,m)

(17)

式中E为整个信号的能量

(18)

这里综合利用时域、频域和能量熵的特征参数。首先，提取信号的11个时域特征参数(T1～T11)和频域的13个频域特征参数(F1～F13)，然后用同样的方法提取Hilbert包络谱的13个频域特征参数，最后，计算IMF分量的能量熵得到6个特征参数，一共得到43个特征参数，其中时域和频域参数如表1所示。

表1 特征参数

2.2 模式识别

在对故障样本进行特征提取后，再利用拉普拉斯特征向量良好的映射能力，对故障数据样本的特征进行相关谱分析，将故障样本特征映射到特征空间蕴涵的几何关系作为分类特征，进而识别故障的类别。基于拉普拉斯特征向量相关谱的滚动轴承故障诊断方法主要步骤为：

(1)将监测对象采集到的数据经信号预处理构成振动信号的样本空间；

(2)分别提取振动信号时域、频域和IMF能量熵的特征，共计43个特征参数，组成特征空间；

(3)计算特征集的拉普拉斯特征向量相关谱，得到相关谱矩阵，组成模式空间；

(4)根据相关谱矩阵分类结果得到诊断信息。

本文方法的最大优点是直接对特征集进行处理，无须再进行故障特征选择，降低了故障诊断的难度。同时，由于故障样本的特征维数在相关谱矩阵中没有体现，从而使得诊断过程和结果直观易理解。

3 应用实例

3.1 滚动轴承故障识别

为了验证本文方法的有效性，用实测滚动轴承故障振动数据进行故障模式识别分析。试验数据采用美国Case Western Reserve University电气工程实验室的滚动轴承试验数据。测试轴承为6205-2RS JEM SKF深沟球轴承，电机负载约为735.5 W，轴承转速为1 772 r/min，试验使用电火花加工技术在轴承上布置单点故障，故障直径为0.355 6 mm，深度为0.279 4 mm，在此情况下采集到正常、内圈单点电蚀、外圈单点电蚀和滚动体单点电蚀4种状态的振动信号，信号采样频率为12 kHz，数据样本长度为2 048。用A,B,C,D四个字母分别代表轴承的正常、滚动体故障、内圈故障、外圈故障四种状态，其代表性振动加速度信号如图2所示。

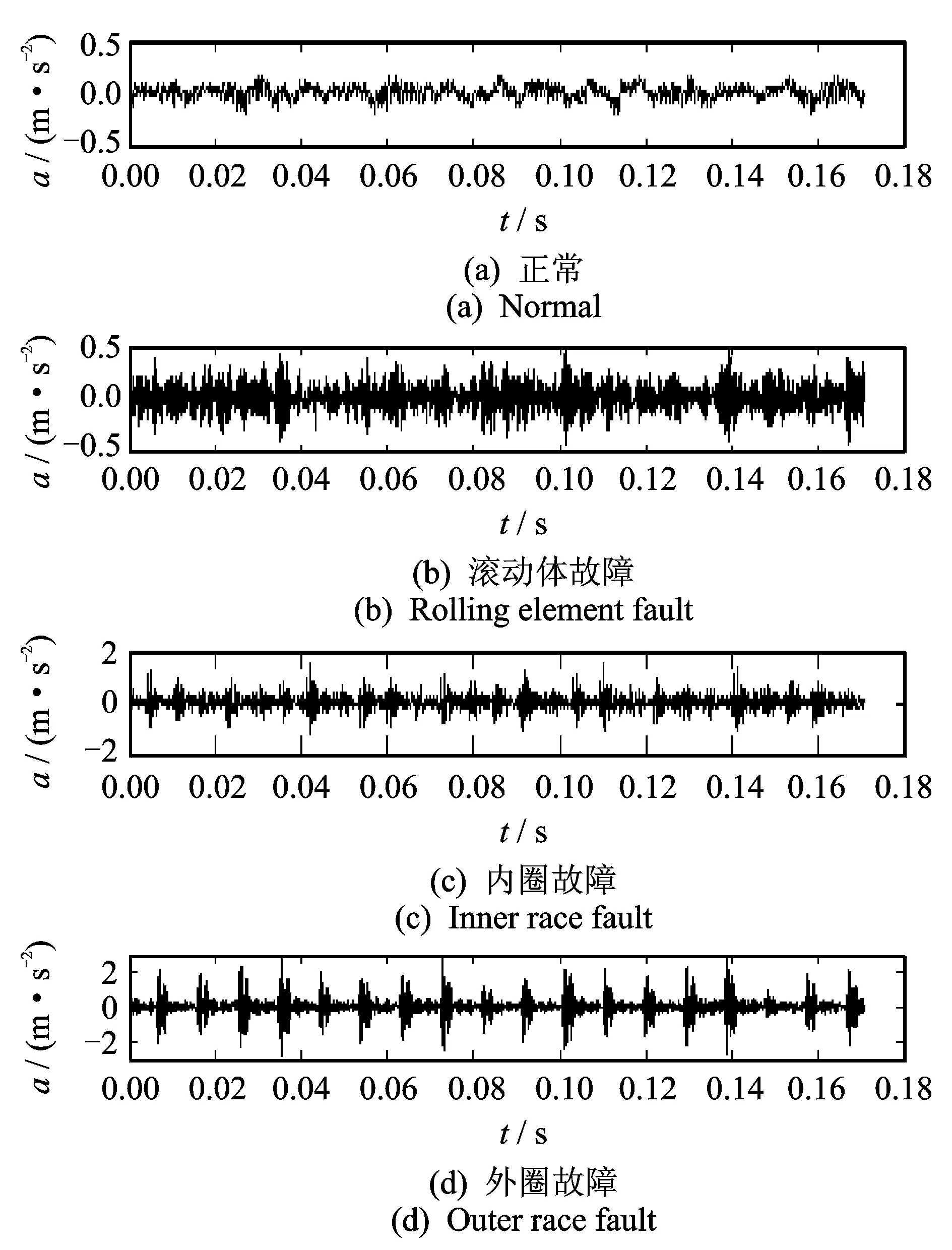
图2 四种不同状态轴承振动信号的时域波形

由于诊断结果的表示形式是矩阵，所以本文仅分别取A,B,C,D四种状态的样本各5个，共计20个样本进行实验。在四种状态中各取1个样本作为已知样本，其余样本作为测试样本。

样本空间分两部分组成：前4个样本由已知样本按照A，B，C，D顺序排列；其余16个样本由测试样本随机排列，组成20×2 048的样本空间；其次，对其进行特征提取，每个样本提取43个特征，组成20×43的特征空间；最后，根据拉普拉斯特征向量相关谱的计算方法得到20×20相关谱矩阵R。由于R中大部分数值的数量级都在10-8以下，所以令阈值ε=10-8，取两位有效数字，得到优化后的相关谱矩阵R′，如图3所示。

在图3中，左上角的4×4单位矩阵表示4种状态的已知样本。由于相关谱矩阵是对称矩阵且只有4种状态，因此根据同一行或者同一列的非0元素属于同一类的判别准则，观察矩阵的前4列或者前4行即足以识别故障类别。以观察相关谱矩阵的前4列为例：第1列的第6,8,11,17个元素非0，同为A状态；第2列的第5,12,13,18个元素非0，同为B状态；第3列的第7,9,14,20个元素非0，同为C状态；第4列的第10,15,16,29个元素非0，同为D状态，与实际情况一致。可见，本文方法可以有效实现滚动轴承故障的分类识别。

3.2 不同故障程度的内圈故障识别

仍采用美国Case Western Reserve University电气工程实验室的滚动轴承试验数据。在同样的实验设备和条件下，内圈故障试验使用电火花加工技术在轴承内圈上布置单点故障，故障直径分别为0.177 8，0.355 6，0.711 2和1.422 4 mm，在此情况下采集到4种状态的内圈单点电蚀的振动信号，信号采样频率为12 kHz，数据样本长度为2 048。用B1,B2,B3,B4分别代表四种直径的内圈故障状态，其振动加速度信号时域波形如下图4所示。

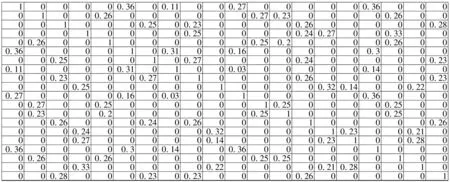
图3 相关谱矩阵R′

取4种状态的样本各5个，共计20个样本进行不同故障程度的内圈故障识别实验。在4种故障状态中各取1个样本作为已知样本，其余样本作为测试样本。

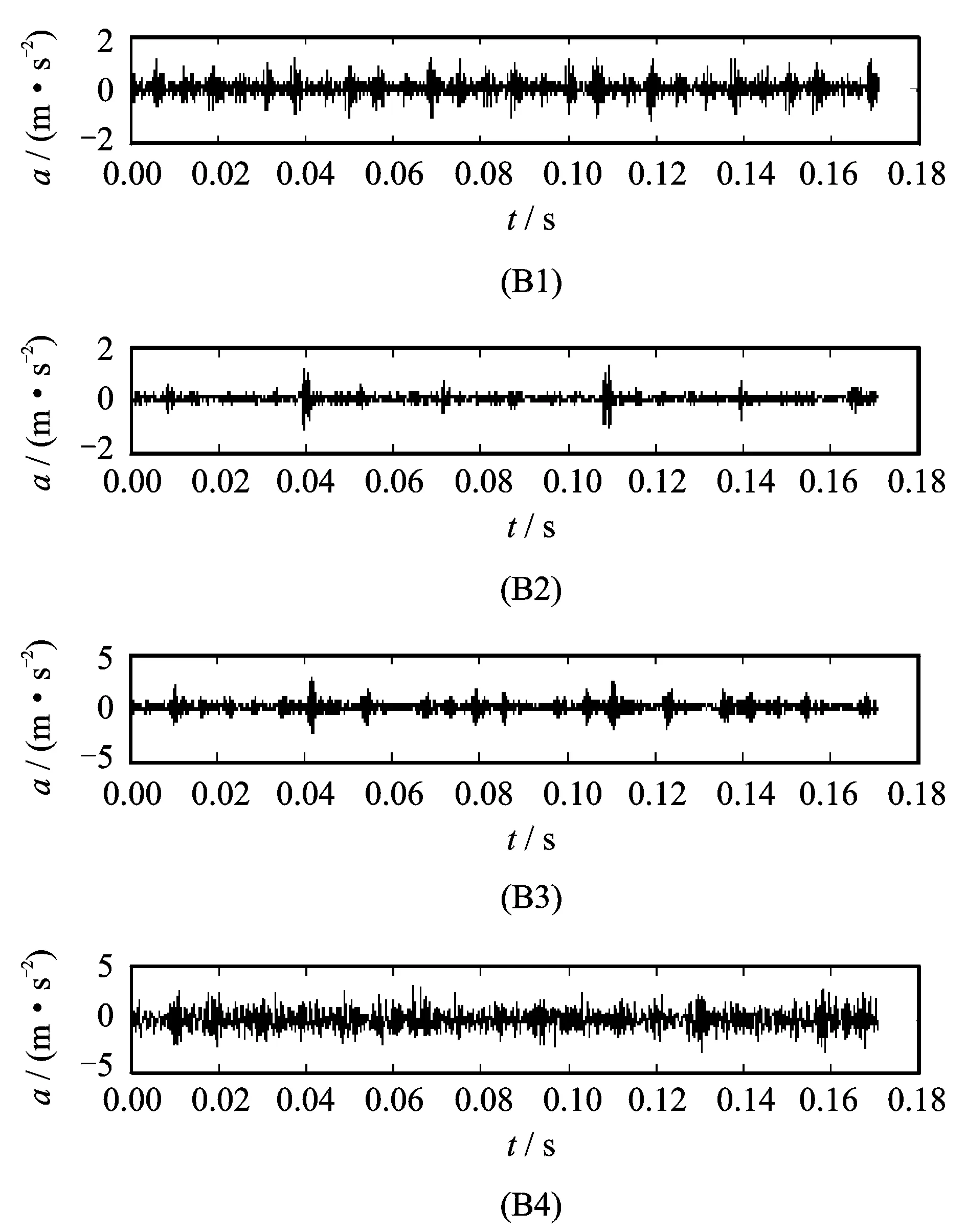
图4 4种不同故障直径的轴承内圈故障振动信号时域波形

样本空间分两部分组成：前4个样本由已知样本按照B1,B2,B3、B4顺序排列；其余16个样本由测试样本按照故障类别的顺序排列，组成20×2 048的样本空间；其次，对其进行特征提取，每个样本提取43个特征，组成20×43的特征空间；最后，根据拉普拉斯特征向量相关谱的计算方法得到20×20相关谱矩阵RB。由于RB中大部分数值的数量级都在10-11以下，所以令阈值εB=10-11，取两位有效数字，得到优化后的相关谱矩阵RB′，如图5所示。

在图5中，左上角的4×4单位矩阵表示4种状态的已知样本，观察相关谱矩阵的前4列：第1列的第5,6,7,8个元素非0，同为B1状态；第2列的第9,10,11,12个元素非0，同为B2状态；第3列的第13,14,15,16个元素非0，同为B3状态；第4列的第17,18,19,20个元素非0，同为B4状态，与实际情况一致。可见，本文方法可以有效实现不同故障直径的滚动轴承内圈故障的分类识别。

4 讨 论

(1)在相关谱矩阵中任选1列(行)进行分析判断，有以下三种情况

a)该列(行)元素全部小于阈值ε，表明该列(行)不含有故障样本间的相关谱信息，所以不能用于故障的分类识别；

b)该列(行)元素中存在大于阈值ε的元素，但不含有已知样本的指导信息，所以只能进行样本的分类，不能进行样本故障类别的识别；

c)该列(行)元素中存在大于阈值ε的元素，且含有已知样本的指导信息，可用于样本故障类别的识别。

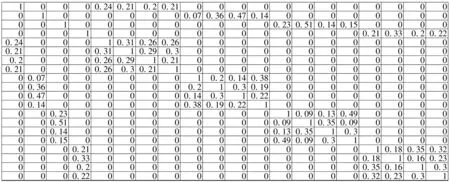
图5 相关谱矩阵RB′

本文滚动轴承故障识别应用实例中，滚动轴承状态类别有4种，因此，只有选取带有已知样本的4列或者4行才能完整地进行故障的分类和识别。

(2)滚动轴承状态特征集是由时域、频域、包络谱和IMF能量熵4部分共计43个特征参数组成。选取不同的特征参数，其分类精度也不同。以a,b,c,d四种特征集进行分析，其中特征集a只提取时域特征；特征集b提取时域和频域特征；特征集c提取时域、频域和包络谱特征；特征集d提取时域、频域、包络谱和IMF能量熵特征。对滚动轴承故障识别应用实例，4种特征集下选取的相关谱矩阵阈值ε如表2所示。

表2 不同特征集下的相关谱矩阵阈值

从表2可以看出，特征集a由于提取的特征太少，相关谱矩阵不能正确进行轴承故障分类；而与特征集b,c,d对应的相关谱矩阵均能正确进行轴承故障分类，且随着特征集提取的特征数的增加，相关谱矩阵分类的阈值相应减小，表明相关谱矩阵的分类精度也逐步提高。

(3)对滚动轴承故障识别应用实例取4个已知样本进行平行试验，其中测试样本分别取4个、8个和12个，分类结果和实际情况完全一致，进一步说明了方法的有效性。

5 结 论

本文提出了拉普拉斯特征向量相关谱，并将其应用于旋转机械故障诊断。该方法通过对原始故障信号进行特征提取，将复杂多维的原始样本空间投影到相互正交的特征空间，根据特征向量的相关谱矩阵进行故障判别与诊断。主要结论如下：

(1)拉普拉斯特征向量相关谱定义为拉普拉斯矩阵特征向量之间夹角余弦的绝对值，它是通过对特征集的拉普拉斯矩阵进行标准正交分解得到的，具有计算过程简单、运算速度快等特点。

(2)基于拉普拉斯特征向量相关谱的滚动轴承故障诊断方法根据相关谱矩阵中已知样本所在的行或列来进行故障的分类识别，随着特征集中特征数的增加，相关谱矩阵的分类精度也相应提高。该方法的特点是将故障模式识别问题转化为求解特征值问题，分类精度高。应用实例验证了该方法的可行性和有效性。

(3)应该指出，拉普拉斯特征向量相关谱的适用性依赖于具体问题，在故障诊断中的应用还存在算法控制参数的有效选择问题，如近邻参数k和热核参数t的选择等。如何自适应地选择最优参数尚需进一步研究。

参考文献：

[1] Diallo D, Benbouzid M E H, Hamad D, et al. Fault detection and diagnosis in an induction machine drive: A pattern recognition approach based on Concordia stator mean current vector[J]. IEEE Trans. Energy Convers, 2005,20(3):512—519.

[2] Beniz R, Sutera A, Vulpiani A. The mechanism of stochastic resonance[J]. The Journal of Physical A, 1981,14(11):4 453—4 572.

[3] HU Qinghua, LIU Jinfu, YU Daren. Mixed feature selection based on granulation and approximation[J]. Knowledge Based Systems, 2008,21(4):294—304.

[4] JACK L B, NANDI A K, MCCORMICK A C. Diagnosis of rolling element bearing faults using radial basis function networks[J]. Applied Signal Processing, 1999,6:25—32.

[5] Hyun Joon Shin. One-class support vector machines-an application in machine fault detection and classification[J]. Computers & Industrial Engineering, 2005,48:395—408.

[6] FEI Shengwei, ZHANG Xiaobin. Fault diagnosis of power transformer based on support vector machine with genetic algorithm[J]. Expert Systems with Applications, 2009,36(8):11 352—11 357.

[7] Andrew Y Ng, Michael Jordan, Yair Weiss. On spectral clustering: analysis and an algorithm[J]. Advances in Neural Information Processing Systems, 2001,14：849—856.

[8] 孔敏,汤进,罗斌.基于拉普拉斯图的谱特征的图像聚类研究[J].中国科学技术大学学报,2007,37(9):1 125—1 129.KONG Min, TANG Jin, LUO Bin. Image clustering based on spectral features of Laplacian graph[J]. Journal of University of Science and Technology of China, 2007,37(9):1 125—1 129.

[9] JIANG Quansheng, JIA Minping, HU Jianzhong, et al. Machinery fault diagnosis using supervised manifold learning[J]. Mechanical Systems and Signal Processing, 2009,23(7):2 301—2 311.

[10] YU Jianbo. Bearing performance degradation assessment using locality preserving projections[J]. Expert Systems with Applications, 2001, 38(6):7 440—7 450.

[11] YU Jianbo, LIU Meifang, WU Hao. Local preserving projections-based feature selection and Gaussian mixture model for machine health assessment[J]. Proceedings of the Institution of Mechanical Engineers, Part C, Journal of Mechanical Engineering Science, 2011,225(7):1 703—1 717.

[12] Chung F R K. Spectral Graph Theory[M]. Fresno: American Mathematical Society, 1997.

[13] Mari C V Nascimento, Andr C P L F De Carvalho. Spectral methods for graph clustering: A survey[J]. European Journal of Operational Research, 2011,211(2):221—231.

[14] LEI Yaguo, HE Zhengjia, ZI Yanyang. A new approach to intelligent fault diagnosis of rotating machinery[J]. Expert Systems with Applications, 2008,35:1 593—1 600.