两种k－ω型湍流模型在无网格方法中的应用研究

蔡晓伟，谭俊杰，王园丁，任登凤，WANG Huasheng，石 清

（1.南京理工大学 能源与动力工程学院，江苏 南京 210094；2.伦敦玛丽皇后大学 材料科学与工程学院，英国 伦敦 E14NS；3.中国空气动力研究与发展中心，四川 绵阳 621000）

0 引 言

随着计算机计算能力的不断提高，计算流体力学（CFD）在实际工程应用中扮演的角色也越来越重要，同时也面临着越来越复杂的问题。高质量网格（计算精度高、计算效率高、收敛性好）的生成一直是耗费人力和机时的难题。无网格方法［1］摒弃了传统CFD方法的网格概念，其计算区域只涉及离散点的布置，因而越来越受欢迎。

在模拟湍流甚至是层流流动时，由于近壁面附近高度各向异性点云的存在，传统无网格法很难准确地拟合空间导数。Munikrishna在近壁区采用格林－高斯公式代替最小二乘法，耦合BL（Baldwin－Lomax）湍流模型，模拟了包括两段翼型在内的一系列流动问题［2］。王刚等采用相似的方法，对高雷诺数下的绕流进行了模拟，取得了较好的结果［3］。点云重构技术是在局部计算区域对高度各向异性的点云进行转化重构，从而形成适合于移动最小二乘无网格法的近各向同性的点云结构，已在层流的数值模拟中取得了较好的效果。

在工程湍流问题中得到广泛应用的是涡粘性模型。BL模型对大多数的附体流动和弱分离流动都具有较高的准确性和可靠性，但对于大多数分离流动却很难准确模拟。k－ω模型是最为人所知和应用最为广泛的两方程涡粘性模型之一，该模型主要求解湍动能k及其比耗散率ω的对流输运方程，其主要贡献来自于 Wilcox［4］。且k－ω 型模型对自由剪切湍流、附着边界层湍流和适度分离湍流都有着较高的精度［5］。

本文借鉴k－ω型湍流模型在网格方法中的成功应用，通过对局部计算区域的高度各向异性点云进行重构，提出了一套基于无网格法的湍流计算方案。在此基础上，通过自主编程对广泛应用的两种k－ω型湍流模型（k－ω SST［6］和 k－ω TNT［7］）方程与雷诺平均N－S方程进行解耦计算，比较分析了两种模型在无网格方法中的湍流预测能力。

1 控制方程

使用自由来流参数（如：密度，声速，粘性系数）及特征长度（如：翼型弦长）对控制方程无量纲化，则二维雷诺平均N－S方程可以表示为：

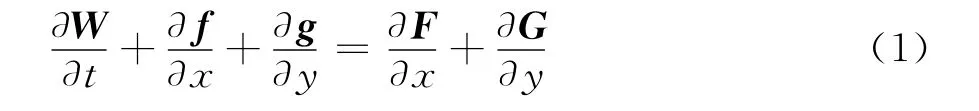
式中，W 为守恒变量，f和g为无粘通量，F和G为粘性通量。其具体表达形式如下：

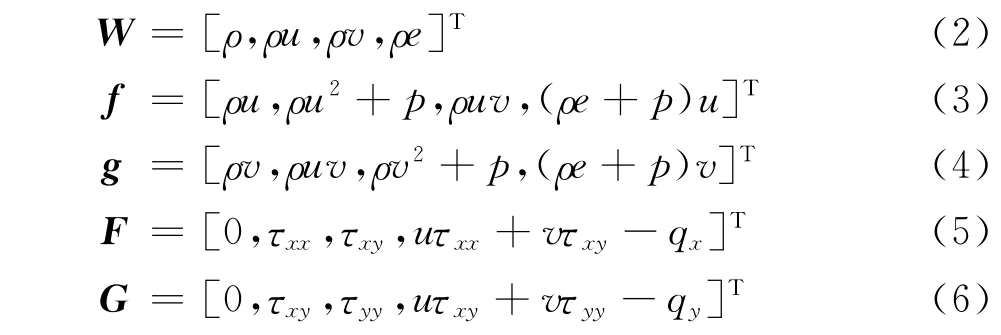
在粘性通量表达式中，剪切应力和热通量可以表示为：

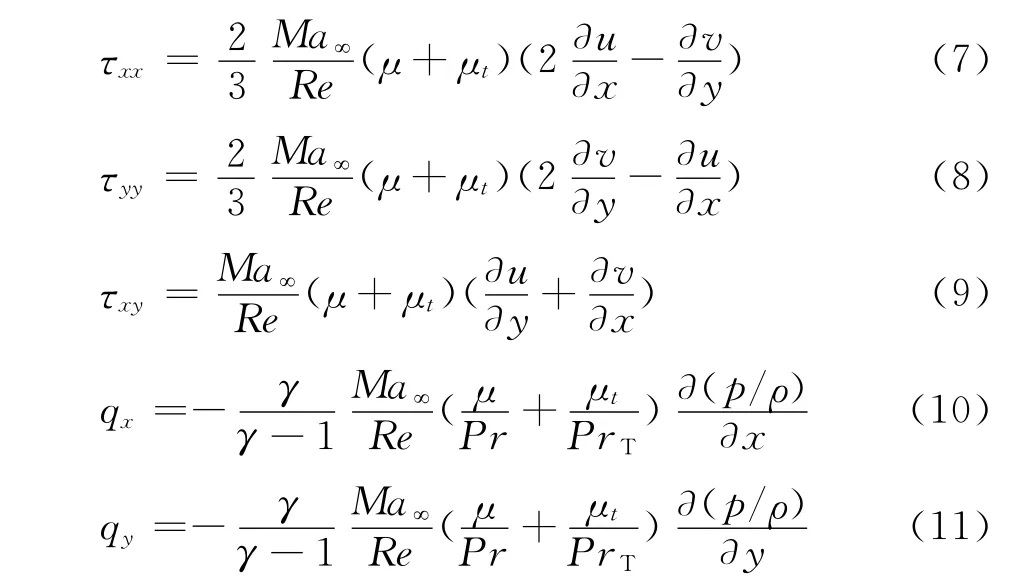
本文数值计算时，取γ＝1.4；Pr＝0.72；PrT＝0.90。层流粘性系数μ利用Sutherland公式计算得到，湍流粘性系数μt由湍流模型提供。

2 湍流模型

k－ωSST模型在近壁面采用k－ωWilcox模型，在边界层边缘和自由剪切层采用标准k－ε模型，其间通过一个混合函数来转换。k－ωTNT模型通过假定湍流区与非湍流区的界面存在一个弱解，从而推导出一套不同于k－ωWilcox模型的参数。两种湍流模型都是基于k－ω湍流模型的改进，在保证对近壁面湍流预测的准确性的同时，通过不同的途径解决了k－ω模型对于自由来流条件的依赖性。为方便比较异同，本文列出了两种模型的表达式：

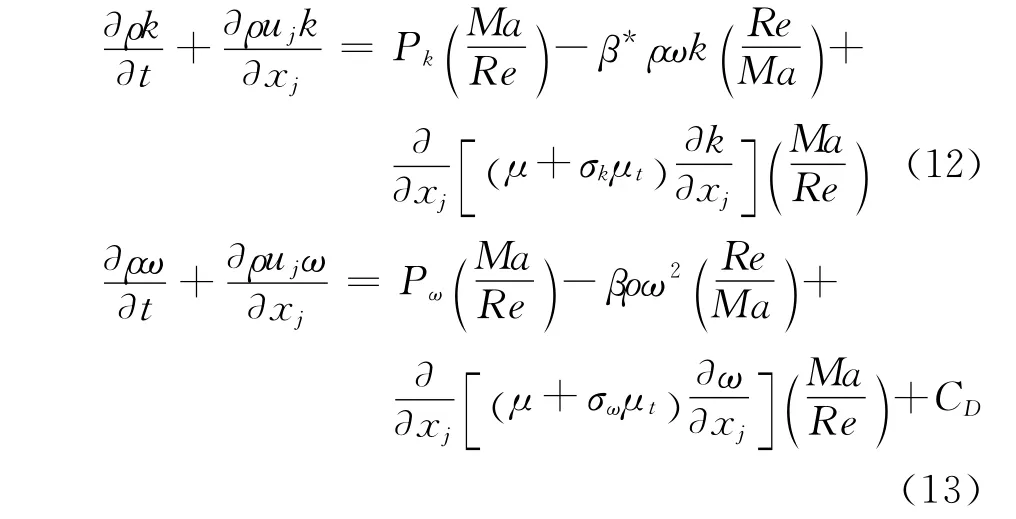
β＊为模型系数，取β＊＝0.09。CD为交叉扩散项，两种模型处理形式不同，将在下文中详细表述。Pk、Pω分别为湍动能k和比耗散率ω的生成项，其表达式为：

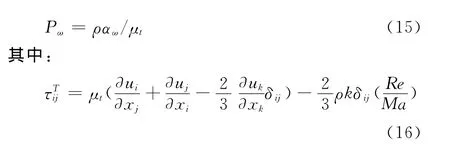
2.1 k－ωSST模型

k－ωSST模型与一般的两方程模型最大的不同之处在于混合函数的应用。交叉扩散项CD以及湍流粘性系数μt的表达式如下：

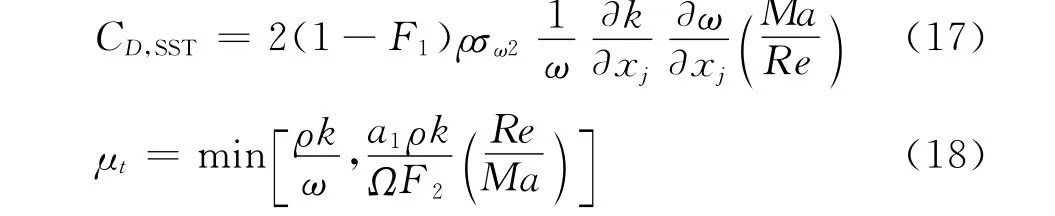
混合函数的构成以及其他参数值详见文献［6］。

2.2 k－ω TNT模型

k－ωTNT模型的交叉扩散项CD为：

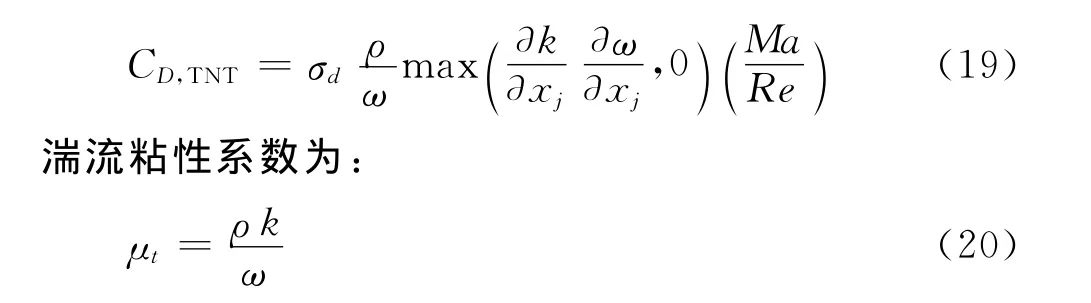
k－ωTNT模型中的具体参数详见文献［7］。

通过对两种湍流表达式的比较，可以看出不同的处理思维：k－ωSST利用到壁面距离的差异，通过混合函数实现两种湍流模型（k－ω Wilcox与k－εStandard）的过渡，原理简单，但形式表达复杂，计算量大。k－ωTNT采用不同于原始k－ω模型的参数，原理较为复杂，但表达式更为简单，计算效率高。

3 数值方法

无网格算法根据离散控制方程的形式可以大致分为积分型和非积分型。积分型无网格法用数值积分来求解控制微分方程的弱解形式，例如：无网格伽辽金法（EFG）、扩散单元法（DEM）以及hp－clouds法等。非积分型无网格法根据节点信息进行偏导数的拟合求解。移动最小二乘法拟合空间导数是目前在计算流体力学中得到广泛应用的无网格方法之一［8］。

3.1 移动最小二乘空间导数拟合

在计算区域内，根据需要布置有限个离散点，并将其标记为i＝1，2，…，np。对于每一个离散点，可以搜索出它的卫星点，记为Ci，如图1所示。与网格方法不同的是，无网格的计算模板没有特殊的空间拓扑结构，只存在点与点之间的联系。使用最小二乘法拟合中心点i的空间导数，需要满足以下的两个条件：

（1）模板中卫星点的数目需大于空间维数；

（2）模板中所有卫星点不能共处一条直线上。

假设u（x，y）为计算区域内任一空间离散点的流场值，则可以基于泰勒级数展开：

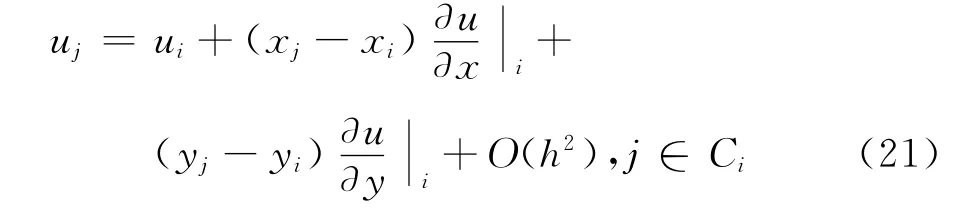
空间导数由移动最小二乘法则决定：

式（22）的解可以写成下面的矩阵形式：

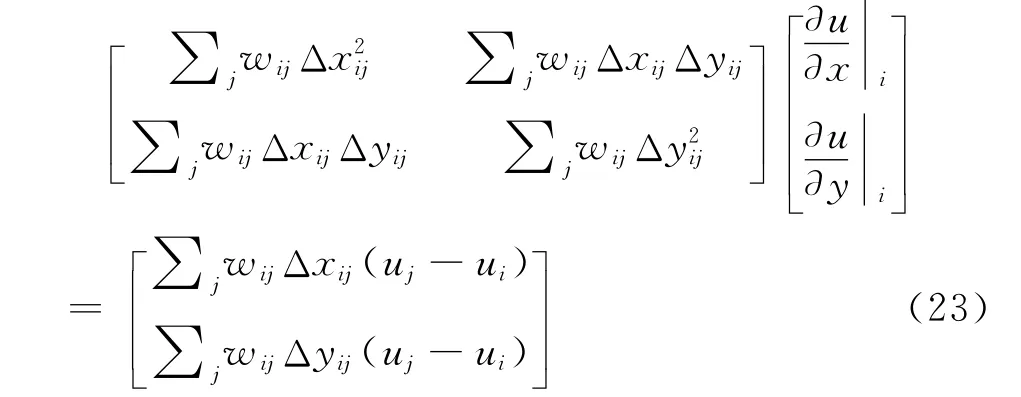
对矩阵进行显式求解，并写成下面的形式：

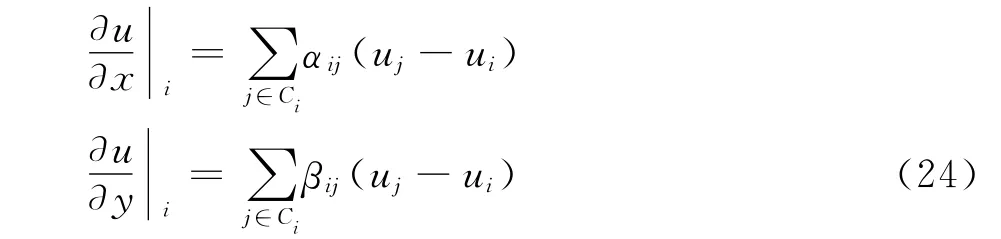
系数αij、βij具体表达由文献［9］给出。

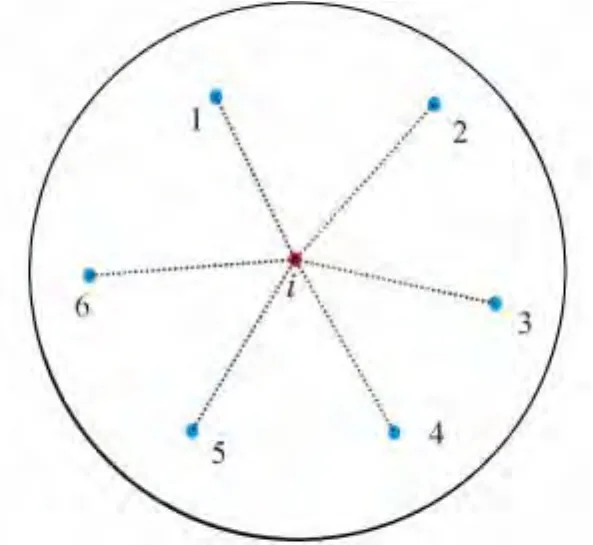
图1 各向同性点云结构示意图Fig.1 Isotropic structure of cloud of points

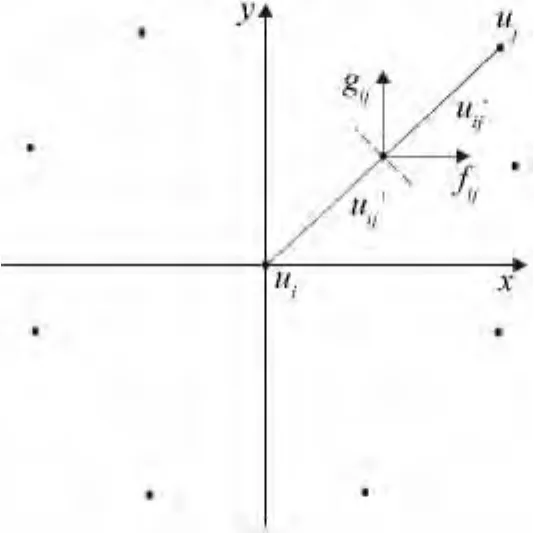
图2 通量求解示意图Fig.2 Illustration for flux calculation

对于式（1）的对流项，可以采用多种成熟的迎风格式计算通量。鉴于本文算例的计算范围是从不可压流动到可压缩跨声速流动，AUSM＋－up［10］格式除保留原始AUSM格式间断、激波、粘性分辨率好的优势外，通过改进原始AUSM格式的压力项和数值声速项，使其能够适应更广马赫数范围的模拟。因此，本文的数值通量（图2中的fij与gij）用AUSM＋－up格式计算。式（1）中的粘性通量中包含了速度和温度的梯度，这两种梯度可以通过式（24）直接计算出。求点ij的粘性通量时，为避免产生奇偶失联，本文对代数平均的梯度值进行修正。

利用最小二乘无网格法空间离散后，式（1）变成一个常微分方程。此时，时间推进求解格式可以借鉴网格算法中成熟的应用。本文选择三阶SSP（Strong Stability Preserving）型Runge－Kutta格式，并使用局部时间步长推进求解。

3.2 点云重构方法

对于一般性湍流流动，物面法向的流场梯度变化要比切向的更为剧烈。此时，为减少计算代价，一般在物面法向上的离散点间的距离比切向要小很多，甚至是10－3以上量级的差距。这样，就会导致在局部计算区域出现高度各向异性的点云结构，而式（23）的条件系数会达到105量级。这时的矩阵系统是病态的，很难准确地进行空间导数拟合。

只有大幅度地减少矩阵条件数，才能使得流场得以稳定地、准确地迭代到收敛值。点云重构技术利用了无网格方法布点灵活的特点，对各向异性点云结构中的卫星点进行增删，从而使得矩阵条件数接近1（健康矩阵系统的条件数）。如图3所示，点i为计算点，卫星点1、2、3、4、5、6、7、8形成了各向异性的点云结构（卫星点2、7到计算点i的距离为其余卫星点的10－3倍）。假设卫星点离计算点i最短距离为R，以R＋δ（δ为极小正数）为半径，以离散点i为原点，构建紧支域，并与卫星点和计算点的连线相交，从而形成新点1′、3′、4′、5′、6′、8′。加上原先的两个点2（2′）和7（7′），这样，一套新的近各向同性的点云结构便形成了。

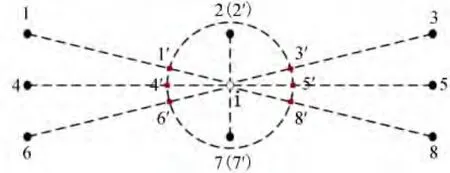
图3 点云重构示意图Fig.3 Illustration for cloud of points reconstruction

采用点云重构技术生成的新点，需要插值计算其流场值，才能参与离散点i的空间导数拟合。本文采用工程中常用的拉格朗日插值方法插值计算。如算例4.1及算例4.2中的离散点布置，在翼型近壁区和尾迹区的计算点会出现高度各向异性的点云（点云内部最长、最短距离之比达到4×103），经过点云重构后，会形成健康的最小二乘矩阵系统。经过数值试验表明，此种方法不仅不会产生数值振荡，而且不影响流场的迭代收敛。

4 算例分析

为验证上述无网格算法的可实现性，本文采用该算法模拟了一系列预测湍流的标准算例。计算算例包括：绕NACA0012翼型和RAE2822翼型的亚声速流动和跨声速的激波诱导边界层分离流动以及大分离流的后向台阶流动。对于翼型绕流，按照“C”型贴体网格的生成方法生成空间离散点（见图4）。对于上述的算例，分别用耦合k－ωSST模型和k－ωTNT模型的无网格法进行计算，将结果与实验数据进行了比对，并分析了不同情况下两种湍流模型在无网格方法中的适用性。

图4 NACA0012和RAE2822翼型离散点布置图Fig.4 Point distributions for NACA0012and RAE2822airfoils

4.1 NACA0012翼型绕流

本算例中共计算了两种工况：（a）Ma＝0.5，α＝3.51°，Re＝2.93×106；（b）Ma＝0.799，α＝2.26°，Re＝9.0×106。

近壁面第一层离散点距壁面1.0×10－5（以翼型弦长为无量纲参考尺度），翼型表面共布置256个离散点。远场边界离翼型物面大于10倍弦长，整个计算区域共布置22425个离散点。

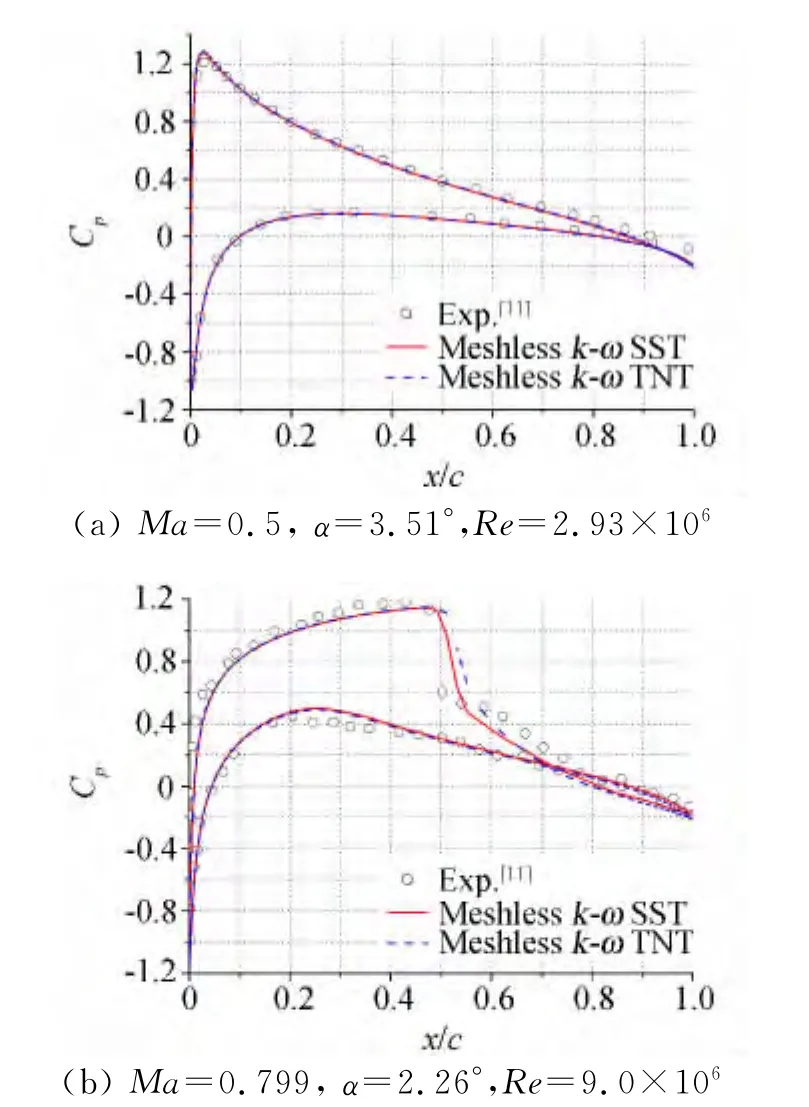
图5 NACA0012翼型表面压力系数分布Fig.5 Pressure coefficient distributions around NACA0012airfoil

基于上述的离散点云布置，采用无网格法分别耦合k－ωSST模型与k－ω TNT模型，计算了（a）、（b）两种工况。图5显示了计算的表面压力系数与文献［11］的实验结果进行的比较。可以发现：最小二乘无网格法在融入点云重构技术后，能够克服边界层内空间导数拟合的困难，成功地耦合两方程湍流模型。对于亚声速的流动，两种k－ω型湍流模型都展示出很好的预测能力，并与实验结果吻合得较好。而对于激波诱导边界分离的跨声速流动，k－ωSST模型所预测的激波位置相比于k－ωTNT模型更接近于实验测量结果，从而显示出更好的激波捕捉能力。

4.2 RAE2822翼型绕流

本文的第二个算例是RAE2822翼型。分别计算了两种工况：（a）Ma＝0.676，α＝1.92°，Re＝5.7×106；（b）Ma＝0.75，α＝2.81°，Re＝6.2×106。

近壁面第一层离散点距壁面1.0×10－5（以翼型弦长为无量纲参考尺度），翼型表面共布置304个离散点。远场边界离翼型物面大于10倍弦长，整个计算区域共布置23985个离散点。

图6给出了两种工况的计算结果与实验数据［12］及网格算法结果［13，15］的对比。当计算条件为亚声速时，两种模型对壁面的压力分布描述几乎没有差别（图6a），下表面的压力系数都和实验数据吻合得很好，而上表面都与实验数据存在一定的差别，前缘吸力峰值都较实验数据略低。当发生激波诱导边界层分离时，k－ωSST模型捕捉激波位置的能力略强于k－ω TNT模型（k－ωSST计算出的激波位置约在52.17%弦长处，k－ωTNT计算出的位置约在54.66%弦长处，实验测量位置约在52.32%弦长处）。另外，两种模型对于激波后的压力预测值都小于实验值。文献［14］基于网格方法耦合k－ω模型计算时也描述了此种差异。当使用更为先进的ν2－f四方程模型［15］时，情况依旧没能得到改观。作者认为：出现此种差异，很可能是因为在文献［13］的实验过程中，人为地设置了转捩点，而本文的模拟中并没有考虑这点。

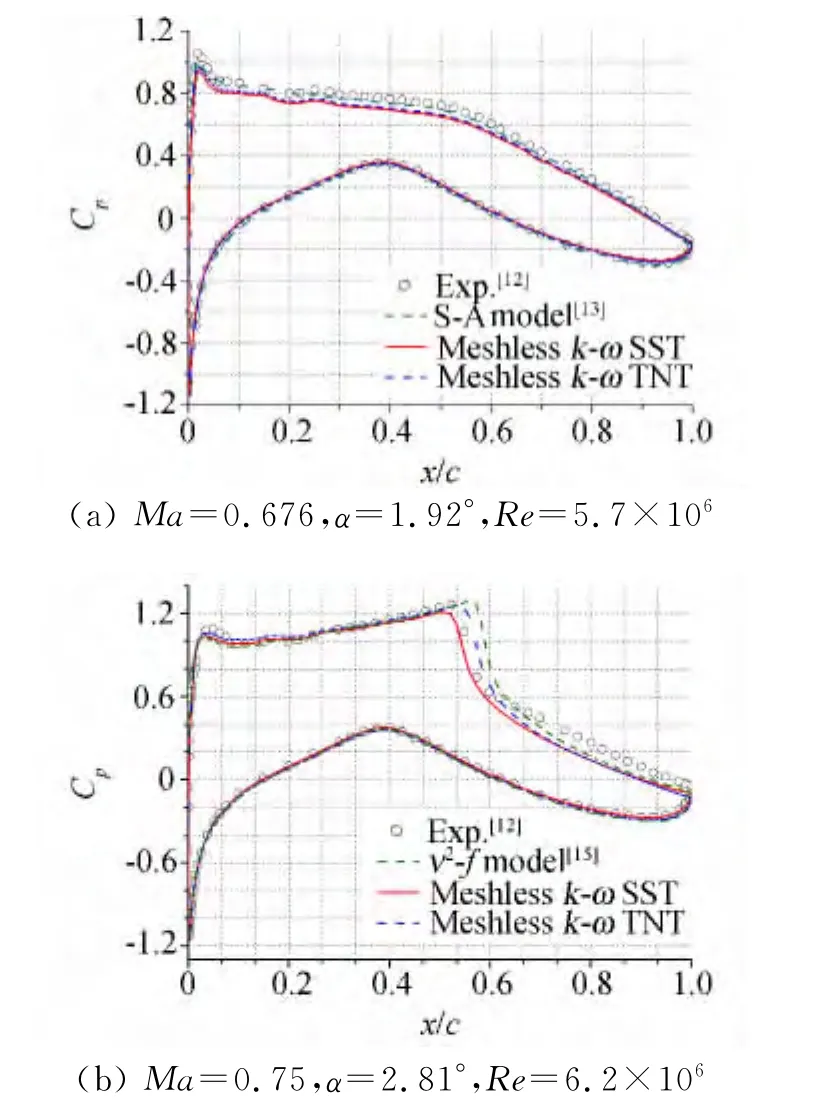
图6 RAE2822翼型表面压力系数分布Fig.6 Pressure coefficient distributions around RAE2822airfoil

4.3 后向台阶大分离流动

后向台阶流动作为大分离的典型流动，早在1981年Standford会议上就确定其为评价湍流模型能力的标准算例。此后，诸多学者运用包含雷诺平均N－S方程方法、大涡模拟方法（LES）和直接数值模拟（DNS）的多种湍流模型，进行了此算例的数值模拟。本文选用该算例的目的是比较在无网格框架下的k－ω SST和k－ωTNT湍流模型的大分离流预测能力。算例的计算工况为：Ma＝0.128，α＝0°，Re＝37423。几何模型如图7所示。表1具体描述了数值模拟的条件参数。与翼型不同的是，该算例以台阶高度（H＝Hs－Hd）为参考长度，上、下表面均采用无滑移边界条件。沿壁面法向等比例推进布点，离散点距离壁面最近距离为1×10－3，固壁面上布点410个，整个计算区域共布点19700个。

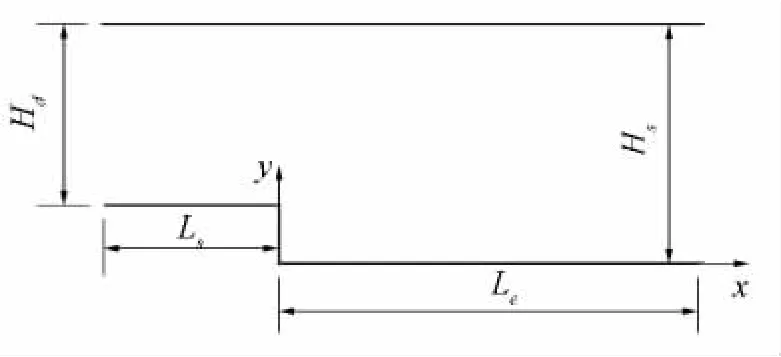
图7 后向台阶几何模型Fig.7 Backward－facing step geometric

表1 后台阶模型计算参数Table1 Flow parameters for backward－facing step

图8描述了分别采用两种湍流模型获得的后向台阶下表面压力系数的分布情况，并与实验数据［16］进行了对比。结果表明：在附着区，两种模型的预测能力相当，且都与实验结果吻合得很好。在恢复区，TNT的计算结果较实验值偏小，SST的计算结果与实验值吻合得较好。图9描述了回流区表面摩擦系数的数值计算结果与实验数据的对比。实验测量得到的回流区长度为6.26 H，SST模型计算出的回流区长度为6.12 H，TNT模型计算出的回流区长度为6.29 H。通过四个不同位置的速度型的对比（图10）进一步验证了上述的结论：在附着区（x／H＝－4.0），两种模型获得的速度型几乎一致；在回流区（x／H＝2.5），TNT模型获得的速度型略优于SST；在恢复区（x／H＝8.0，x／H＝32.0），则反之。

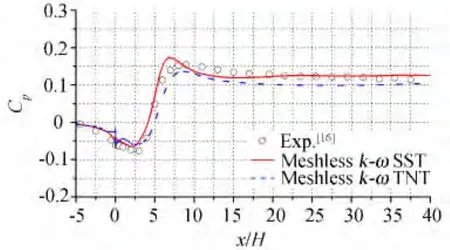
图8 下表面压力系数比较Fig.8 Comparison of pressure coefficient along the bottom wall

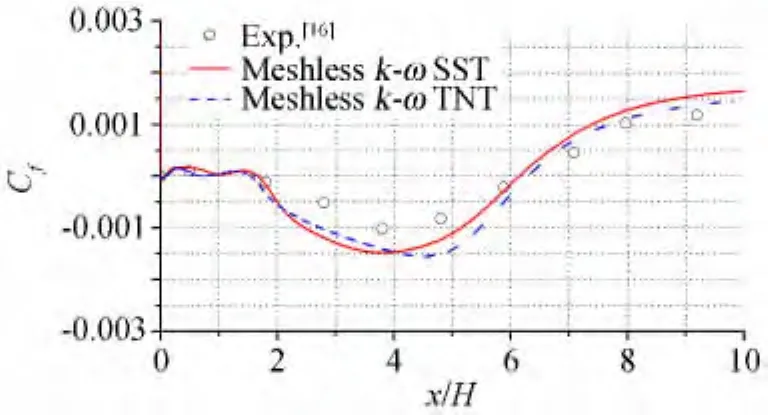
图9 回流区摩擦系数比较Fig.9 Comparison of the friction coefficient in the recirculation region

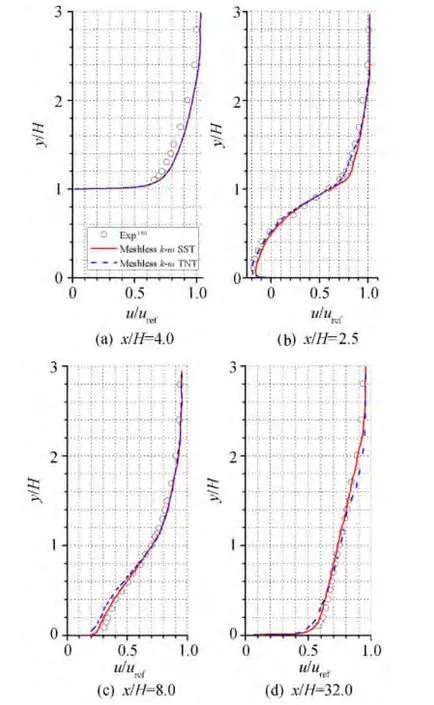
图10 平均流速度剖面Fig.10 Streamwise mean velocity u－profiles

5 结 论

本文采用无网格点云重构技术，克服传统最小二乘法拟合空间导数的困难，成功耦合k－ωSST和k－ω TNT湍流模型，实现了最小二乘无网格法框架下的湍流流动的数值模拟。通过对弱逆压梯度分离、激波诱导分离和大分离流动条件下的数值模拟，比较分析了两种模型在无网格框架下的湍流预测能力。结论如下：

（1）对因弱逆压梯度产生的分离流动，两种湍流模型的预测能力相当。而TNT模型因为表达形式简单，因而较SST模型更具效率性。

（2）对激波诱导分离的流动，SST模型捕捉激波的能力更强。

（3）对于大分离的流动，在附着区和恢复区，SST的计算结果更接近于实验值。在回流区，TNT的计算结果与实验值吻合得更好。

综上，本文拓宽了移动最小二乘无网格法在湍流研究方向的应用，并通过对三种不同程度的分离流进行了初步的模拟与分析，为模拟不同情况下的湍流选用合适的湍流模型提供了进一步的参考。

［1］BATINA J.A gridless Euler／Navier－Stokes solution algorithm for complex two－dimensional application［R］.NASA TM 107631，1992.

［2］MUNIKRISHNA N，BALAKRISHNAN N.Turbulent flow computations on a hybrid Cartesian point distribution using meshless solver LSFD－U［J］.Computers ＆ Fluids，2011，40：118－138.

［3］WANG G，YE Z Y，JIANG C Q，et al.Gridless method for Navier－Stokes equations with high Reynolds number［J］.Chinese Journal of Applied Mechanics，2007，24（3）：348－352.（in Chinese）王刚，叶正寅，蒋超奇，等.高雷诺数下求解NS方程的无网格算法［J］.应用力学学报，2007，24（3）：348－352.

［4］WILCOX D C.Turbulence modeling in CFD［M］.Third Edition，DCW Industries，Inc.，La Canada，CA，2006.

［5］阎超.计算流体力学方法及应用［M］.北京航空航天大学出版社，2006.

［6］MENTER F R.Two－equation eddy－viscosity turbulence models for engineering applications［J］.AIAA Journal，1949，32（8）：269－289.

［7］KOK JC.Resolving the dependence on free－stream values for the k－ωturbulence model［J］.AIAA Journal，2000，38（7）：1292－1295.

［8］CAI X W，TAN J J，MA X J.A 2Dmeshless solver based on AUSM＋and MUSCL scheme［J］.Applied Mechanics and Materials，2012，（105－107）：2140－2143.

［9］SRIDAR D.An upwind finite difference scheme for meshless solvers［J］.Journal of Computational Physics，2003，（189）：1－29.

［10］LIOU M S.A sequel to AUSM，PartⅡ：AUSM＋－up for all speeds［J］.Journal of Computational Physics，2006，214（1）：137－170.

［11］HARRIS CD.Two－dimensional aerodynamic characteristics of the NACA0012airfoil in the Langley 8－foot transonic pressure tunnel［R］.NASA TM 81927，1981.

［12］COOK P H，DONALD M A，FIRMIN M C P.Aerofoil RAE2822pressure distribution，boundary layer and wake measurement［R］.AGARD AR 138，1979.

［13］DELANAYE M，et al.Automatic hybrid－cartesian grid generation for high－Reynolds number flows around complex geometries［R］.AIAA 1999－777，1999.

［14］MORYOSSEF Y，LEVY Y.Unconditionally positive implicit procedure for two－equation turbulence models：application to kωturbulence models［J］.Journal of Computational Physics，2006，220（1）：88－108.

［15］LIEN F S，KALITZIN G.Computations of transonic flow with thev2－fturbulence model［J］.International Journal for Heat and Fluid Flow，2001，22（1）：53－61.

［16］DRIVER D M，SEEGMILLER H L.Features of a reattaching turbulent shear layer in divergent channel flow［J］.AIAA Journal，1985，23（1）：163－171.