一种方向优化最小均方算法

李霄剑 王 永 陈绍青 付志浩



一种方向优化最小均方算法

李霄剑 王 永*陈绍青 付志浩

(中国科学与技术大学自动化系 合肥 230027)

最小均方(Least Mean Square, LMS)算法的更新方向是对最速下降方向的估计，其收敛速度也受到最速下降法的约束。为了摆脱该约束，该文在对LMS算法分析的基础上，提出一种针对LMS算法的分块方向优化方法。该方法通过分析误差信号来选择更新向量，使得算法的更新方向尽可能接近Newton方向。基于此方法，给出一种方向优化LMS(Direction Optimization LMS, DOLMS)算法，并推广到变步长DOLMS算法。理论分析与仿真结果表明，该方法与传统分块LMS算法相比，有更快的收敛速度和更小的计算复杂度。

自适应滤波；最小均方算法；方向优化；最小均方球；方向优化最小均方算法

1 引言

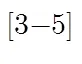
为了优化算法的收敛路径，人们提出了以Newton方向为算法估计方向的LMS-Newton算法[15,16]。对于基本FIR(Finite Impulse Response)滤波器而言，自适应算法的梯度函数为二阶函数，此时Newton方向就是一步最优方向(由当前滤波器参数直接指向最优滤波器参数的向量方向)。LMS- Newton算法具有较快的收敛速度，但同时因算法更新时含有矩阵求逆运算，具有算法计算量大、结构复杂等缺点。

本文分析了LMS收敛原理，提出了新的LMS分块计算方法。新方法选择数据块中最接近Newton方向的更新向量进行更新，无论是收敛速度还是计算量都远优于BLMS的分块方法。基于此方法提出了一种方向优化LMS(Direction Optimization LMS, DOLMS)算法及其相应的变步长算法。DOLMS算法不受最速下降法自身收敛速度的限制，能够更快地收敛到最优点。该算法更新向量的计算公式形式与NLMS完全相同，因此适用于NLMS的变步长优化方法对该算法同样适用。DOLMS算法只是选择其中一个更新向量进行算法更新，省去了求取平均值的过程，因此算法复杂度较BLMS算法而言有了极大的简化。通过仿真分析了DOLMS算法的特性，而后与其它算法进行了比较，仿真结果说明该算法对变步长LMS算法能起到同样的优化作用。

2 LMS算法及其收敛特性分析

2.1 LMS算法及分块LMS算法简介

LMS算法是一种随机梯度算法。它以系统均方误差为代价函数，利用随机估计值代替最速下降法中的梯度向量，在统计意义上以最速下降方向收敛到Wiener解。算法结构如图1所示。

图1 LMS算法结构图

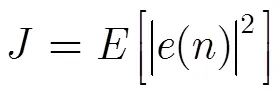
LMS算法权值更新向量为

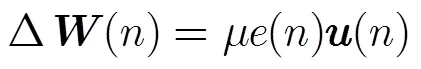
LMS更新公式为

为了优化算法步长，NLMS算法被提出，更新向量为

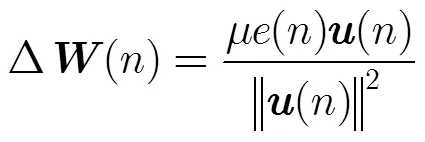
为了更加准确地对最速下降方向进行估计，BLMS算法被提出，更新向量为

其中，为分块长度。

BLMS算法的基本思想是通过增加样本数使得对最速下降方向的估计更加准确，因此增加分块长度只能增加估计的准确性，其收敛速度受最速下降法约束不会有明显加快。

2.2 LMS单步更新方向与更新向量的关系

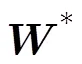
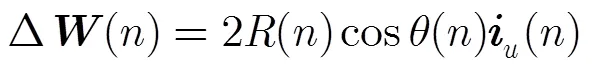
证明 LMS自适应滤波器的系统估计误差可写为

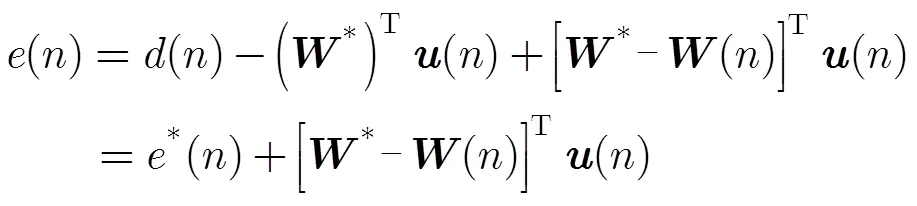
将式(7)代入式(2)可得

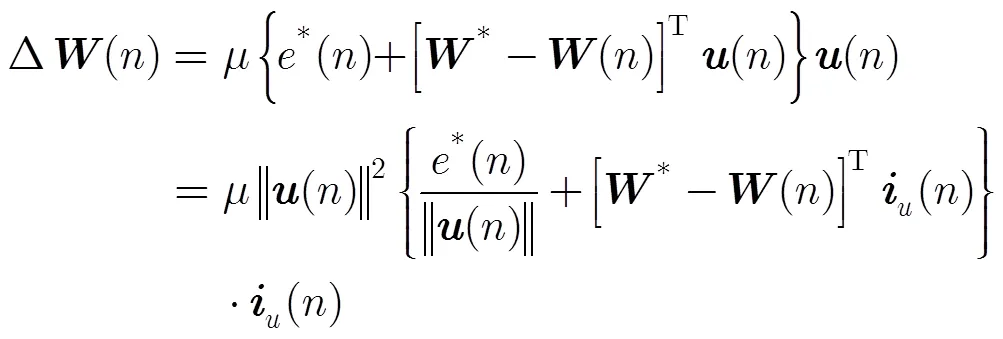
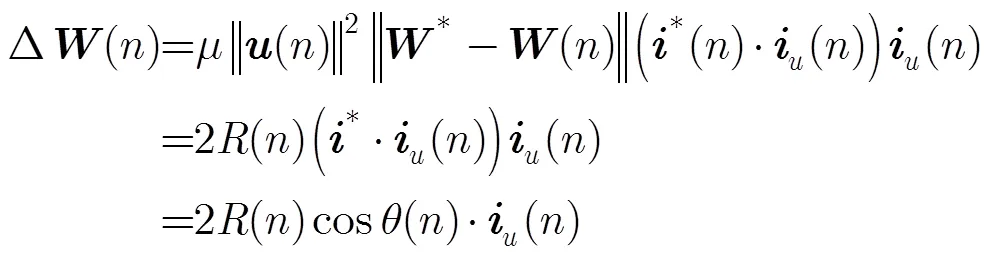
证毕

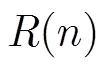
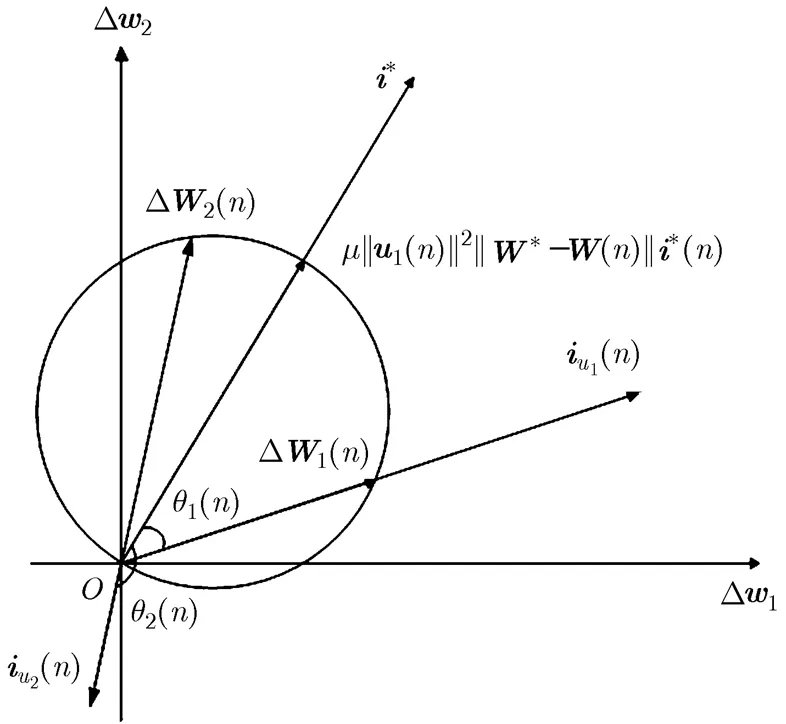
图2 2维LMS球示意图

2.3 分块归一化LMS算法的方向优化

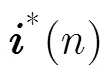
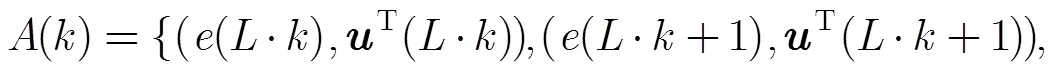
将每一组数据代入式(4)，可以计算得出与之对应的归一化更新向量为

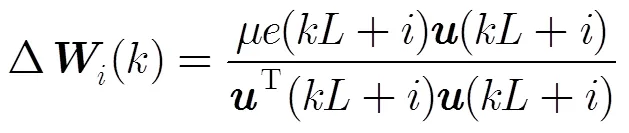
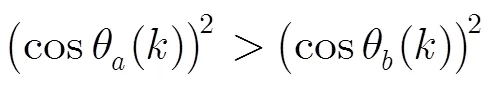
其中，等式左边为系统的归一化误差，式(13)还可写成

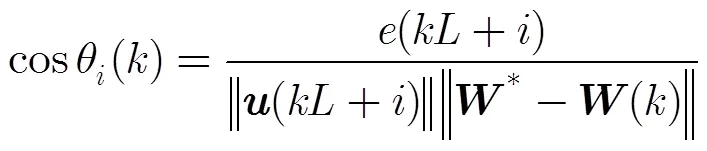
显然，定理2具有递推性，因此很容易得到如下推论：

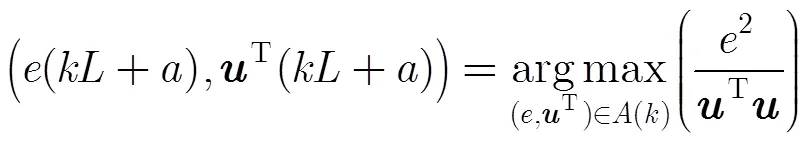
3 方向优化LMS(DOLMS)算法设计

上述分析为比较LMS算法的更新方向提供了依据，也提供了一种新的LMS分块计算的方法。与BLMS不同，新方法是通过选取块中最优的更新向量进行更新，因此摆脱了最速下降法收敛速度的约束，具有更快的收敛速度。

3.1 算法结构

DOLMS算法结构与分块LMS算法类似，其结构如图3所示。

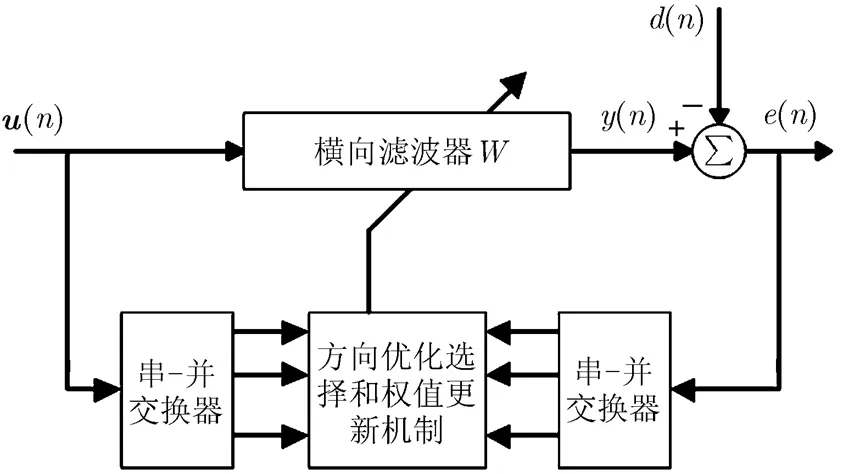
图3 DOLMS算法结构图

根据定理2推论选取更新所需的误差和输入向量：

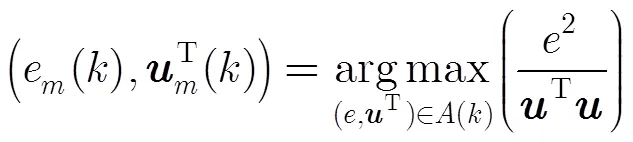
则更新向量为

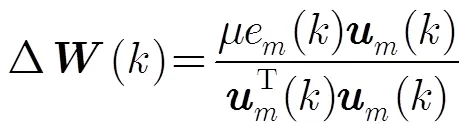
算法步长因子的取值范围与归一化LMS算法相同。

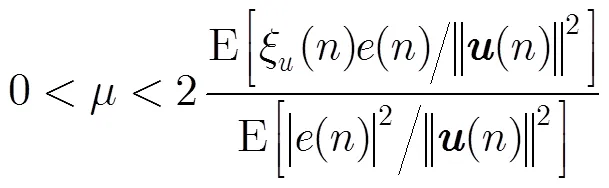
最优步长参数[1,4]为

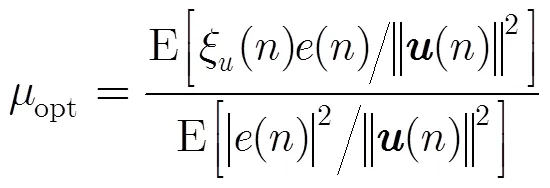
为了保证系统稳态误差，算法还可以采用文献[8]所提出的变步长方法，形成变步长DOLMS算法。变步长为

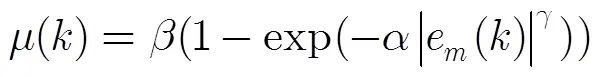
3.2 算法流程

DOLMS的算法流程如下：

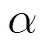
步骤4 计数器加1，判断是否等于：如不等，则跳转至步骤3；反之，继续。

3.3 算法特性理论分析

下面对于DOLMS的特点及其原因进行分析。

(2)块长度与收敛速度的关系 DOLMS虽然分块进行计算，但与BLMS算法相比，其分块的目的并不相同。对于一般分块LMS算法，分块是为了更加准确地估计最速下降方向，增加块长度只能使最速下降方向估计更为准确，其收敛速度受更新方向约束不会加快。然而DOLMS算法进行分块是为了寻找更加接近一步最优方向的更新向量。对于输入为周期信号[17]而言，当块长度等于信号周期，此时DOLMS算法的收敛速度达到最大，增加块长度对算法收敛速度不会有影响。而对于非周期信号而言，随着块长度的增加，其最终选取的更新方向会更为接近一步最优方向，收敛速度也会越快，此时算法存在通过一步更新达到最优值的可能性。

(3)稳态误差 由于该算法取归一化误差平方值最大项进行更新，故当系统输出误差信号存在测量噪声时，此种更新方法会放大噪声对系统更新的影响。特别是在最优点附近，此时输出误差信号的信噪比低，归一化误差的大小更多取决于测量误差而非更新方向，因此DOLMS算法的稳态误差会略大于相同变步长的NLMS算法。

(4)算法复杂度 此处为了展现DOLMS算法复杂度，将其与分块归一化LMS算法、BLMS算法进行比较。

首先考察DOLMS算法复杂度。算法步骤3需要在每个采样周期计算归一化误差平方，故计算归一化误差的复杂度为+2。比较归一化误差平方时，不需要进行乘法运算，复杂度为0。算法步骤5在每一块只需进行一次更新向量的运算，如式(17)，其中向量模长平方已经在归一化误差计算中求得；故更新向量计算复杂度为+2。一个分块周期内算法总体复杂度为：(+2)++2=(+1)(+2)。

需要注意的是， DOLMS算法计算量主要用于计算输入向量模长平方。该计算可以通过记录每次输入值平方进行简化计算，这样每次计算输入向量模长平方只需计算最新的输入值平方，再与之前记录数据求和即可。因此步骤3的计算复杂度可以简化为3。DOLMS算法的整体复杂度就能得到了极大的简化，在一个分块周期内的计算复杂度为3++2。

DOLMS与其它算法的复杂度比较如表1所示。

表1算法复杂度比较

算法名称DOLMSDOLMS(简)分块归一化LMSBLMS 复杂度(L+1)3L+M+2L(2M+1)+M+1(L+1)M+1

从表1可以看出，DOLMS算法的复杂度低于分块归一化LMS算法，略高于BLMS算法。而简化后的DOLMS算法复杂度则远小于另外两种算法。

4 算法比较与仿真

为了验证DOLMS算法的有效性，下面对算法进行仿真，并与归一化块LMS算法[18]，BLMS算法[8]进行比较。仿真将采用以下两种系统模型。

4.1 算法特性分析

DOLMS算法随着块长度的增加，所选取的更新方向会更为接近一步最优方向，收敛速度会随着块长度的增加而变快。分别以=5,=50,=250作为块长度，利用DOLMS对模型1进行仿真试验，统一选取步长因子为=1。重复试验25次，取块平均误差均值的对数作为纵坐标，以更新次数作为横坐标，如图4所示。由图4可以看出，块长度越长其更新速度越快，但同时稳态误差也会随之变大。

同时与大多数LMS算法相同，在块长度不变的情况下，步长因子越小，收敛速度越慢但稳态误差会变小。选取=10作为块长度，分别以=1.0,= 0.5,=0.1作为步长因子，利用方向优化LMS对模型1进行仿真试验，其结果如图5所示。由图5可以看出，随着步长因子的增加，算法的稳态误差随之增大，而收敛速度也随之提高。

4.2 算法仿真比较

统一选取算法步长为10，分别利用方向优化LMS，分块归一化LMS, BLMS对模型1进行仿真试验。其中方向优化LMS，分块归一化LMS的步长为1.00; BLMS算法步长因子取0.09时，算法收敛不平稳会出现大量尖峰，因此选取0.08作为BLMS算法最优步长进行比较。所得结果如图6所示。由图6可以看出DOLMS的收敛速度快于分块NLMS算法和BLMS算法，但其稳态误差有明显增大。

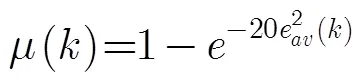
通过上述比较可知，DOLMS算法的收敛速度明显快于分块归一化LMS算法和BLMS算法，其稳态误差经过变步长优化后与同样经过变步长优化后的分块NLMS和BLMS基本相同。由此可看出，对于当前存在大量的变步长LMS算法，DOLMS算法可直接对其进行再次优化。优化后的变步长DOLMS的收敛速度较之原变步长LMS算法而言，其收敛速度有较大提升同时稳态误差有轻微的增大。

对于输入信号为有色信号的LMS自适应算法而言，以最速下降方向为收敛方向往往会导致自适应滤波器权值在接近最优值时收敛速率会不断减慢；这种特性在输入信号为正弦信号时极为明显。基于这种现象，设计出了模型2，将上述3种变步长LMS算法应用于模型2，进行仿真实验，结果如图8所示。

图4 块长度对DOLMS的影响

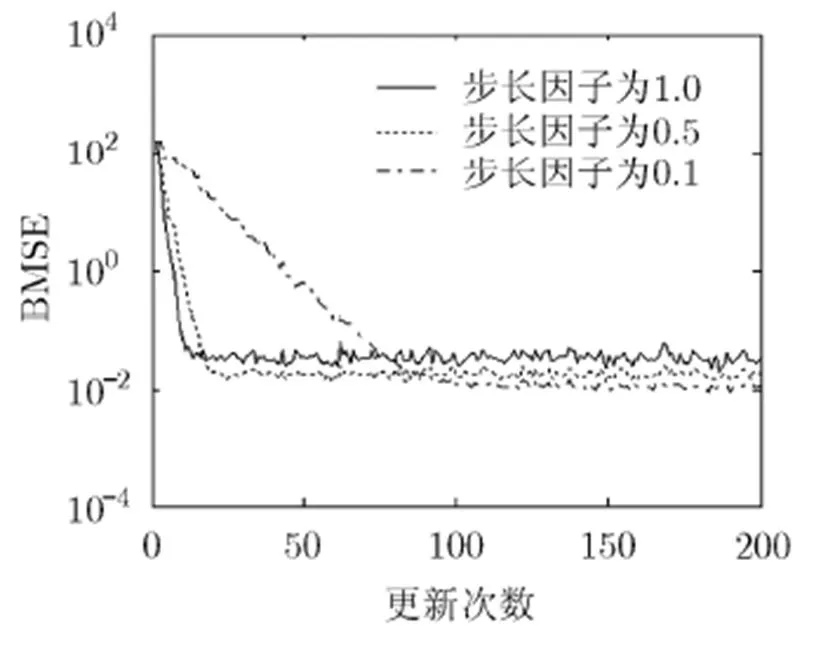
图5 步长因子对DOLMS的影响

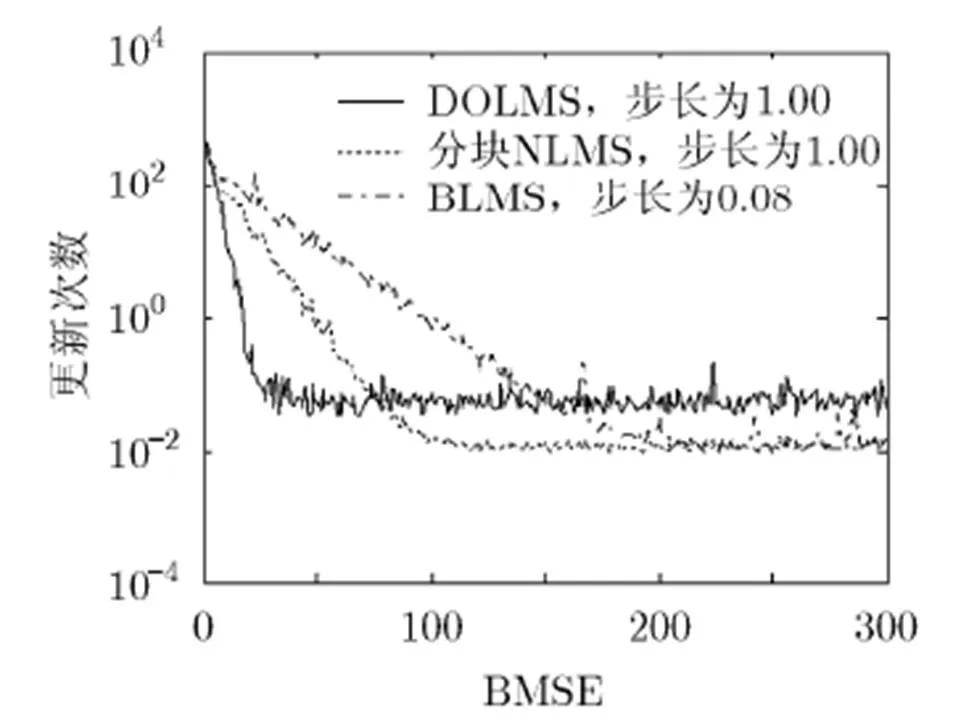
图6 定步长算法比较图

图7 变步长算法比较图

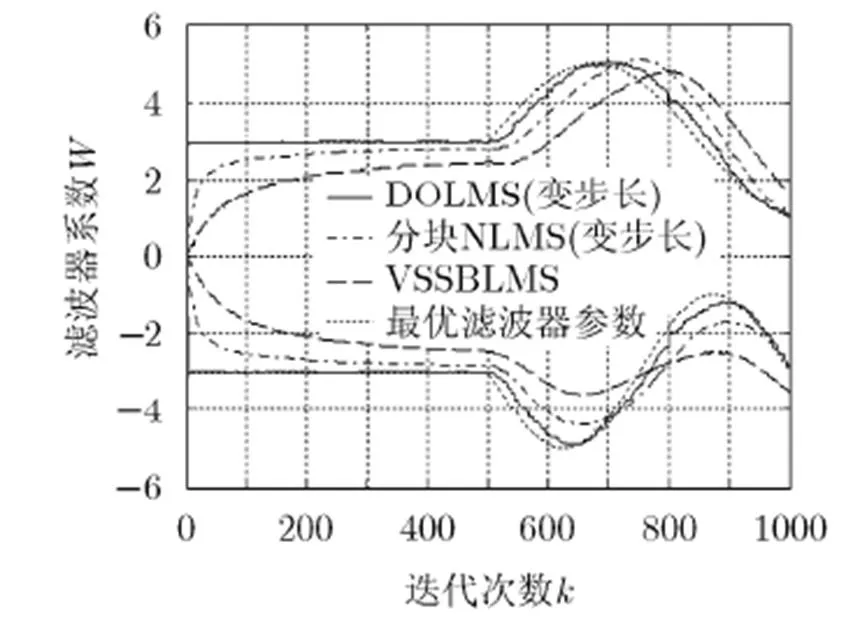
图8 滤波器系数学习曲线

5 结束语

当LMS算法及其改进算法以有色信号作为输入时，其收敛方向为对最速下降方向的估计这一特性，不仅限制了算法步长的选择，同时也限制了算法的收敛速度。本文提出了一种针对分块LMS算法的方向优化方法，并给出了该方法的理论依据。该方法通过分析误差信号选择最接近一步最优方向的更新向量进行算法更新，摆脱了最速下降法的约束。以此方法为基础提出了DOLMS算法，将DOLMS算法与分块NLMS, BLMS算法进行了比较。比较结果表明，DOLMS算法有更快的收敛速度和更小的计算复杂度。且DOLMS算法可以与LMS算法的变步长方法同时使用，在保证收敛速度的基础上优化稳态误差。同时，算法块长度越长收敛速度越快的特点适用于自适应滤波器系数不方便频繁变动的情况，使得每次更新更加有效。

[1] Hayin S. Adaptive Filter Theory[M]. 北京: 电子工业出版社, 2003: 70-267.

[2] Butterweck H J. Steady-state analysis of the long LMS adaptive filter[J]., 2011, 91(4): 690-701.

[3] Duttweiler D L. Proportionate normalized least-mean- squares adaptation in echo cancelers[J]., 2000, 8(5): 508-518.

[4] 曾召华, 刘贵忠, 赵建平. LMS和归一化LMS算法收敛门限与步长的确定[J]. 电子与信息学报, 2003, 25(11): 1469-1474.

Zeng Zhao-hua, Liu Gui-zhong, and Zhao Jian-ping. Determining of convergent threshold and step-size for LMS and normalized LMS algorithm[J]., 2003, 25(11): 1469-1474.

[5] Borisagar K R, Sedani B S, and Kulkarni G R. Simulation and performance analysis of LMS and NLMS adaptive filters in non-stationary noisy environment[C]. International Conference on Computational Intelligence and Communication Systems, Gwalior, 2011:682-686.

[6] Feuer A. Performance analysis of the block least mean square algorithm[J]., 1985, CAS-32(9): 960-963.

[7] 吕春英, 敖伟, 张洪顺. 一种新的变步长LMS算法[J]. 通信技术, 2011, 44(3): 11-14.

Lü Chun-ying, Ao Wei, and Zhang Hong-shun. A new variable step-size LMS algorithm[J]., 2011, 44(3): 11-14.

[8] 肖海英, 何方白. 一种时域变步长BLMS自适应算法[J]. 西南科技大学学报, 2006, 21(2): 30-35.

Xiao Hai-ying and He Fang-bai. A variable step size BLMS adaptive algorithm in time domain[J]., 2006, 21(2): 30-35.

[9] 曲庆, 金坚, 谷源涛. 用于稀疏系统辨识的改进0-LMS算法[J]. 电子与信息学报, 2011, 33(3): 604-609.

Qu Qing, Jin Jian, and Gu Yuan-tao. An improved0-LMS algorithm for sparse system identification[J]., 2011, 33(3): 604-609.

[10] Bismor D. LMS algorithm step size adjustment for fast convergence[J]., 2012, 37(1): 31-40.

[11] Mayyas K. A variable step-size selective partial update LMS algorithm[J]., 2013, 23(1): 75-85.

[12] Cai Wei-ju. A new variable step size LMS adaptive filtering algorithm and its analysis[J]., 2013, 605(2013): 2193-2196.

[13] Ao Wei, Xiang Wan-qin, Zhang You-peng,. A new variable step size LMS adaptive filtering algorithm[C]. International Conference on Computer Science and Electronics Engineering ICCSEE, Hangzhou, 2012, 2: 265-268.

[14] Mayyas K and Momani F. An LMS adaptive algorithm with a new step-size control equation[J]., 2011, 348(4):589-605.

[15] Diniz P S R, de Campos M L R, and Antoniou A. Analysis of LMS-Newton adaptive filtering algorithms with variable convergence factor[J]., 1995, 43(3): 617-627.

[16] Lian Rui-mei. An improved LMS-Newton algorithm and its analysis[C]. International Conference on Mechanical and Electronics Engineering,Hefei, 2011: 458-462.

[17] Parra I E, Hernandez W, and Fernandez E. On the convergence of LMS filters under periodic signals[J].:, 2013, 23(3):808-816.

[18] 魏璀璨, 王永, 陈绍青, 等. 磁悬浮隔振器分块归一化LMS算法控制研究[J]. 振动与冲击, 2012, 31(18): 100-103.

Wei Cui-can, Wang Yong, Chen Shao-qing,. Control of an electromagnetic suspension vibration isolator based on block normalized LMS algorithm[J]., 2012, 31(18): 100-103.

李霄剑： 男，1990年生，硕士生，研究方向为自适应滤波、振动主动控制.

王 永： 男，1962年生，教授，博士生导师，研究方向为振动主动控制、飞行器制导与控制等.

陈绍青： 男，1985年生，博士，研究方向为自适应滤波、振动主动控制等.

A Direction Optimization Least Mean Square Algorithm

Li Xiao-jian Wang Yong Chen Shao-qing Fu Zhi-hao

(,,230027,)

The update vector of Least Mean Square (LMS) algorithm is an estimation of the gradient vector, thus its convergence rate is limited by the method of steepest descent. Based on the discussion of basic LMS, a direction optimization method of LMS algorithm is proposed in order to get rid of this speed constraint. In the proposed method, the closest update vector to the Newton direction is chosen based on the analysis of the error signal. Based on the method, a Direction Optimization LMS (DOLMS) algorithm is proposed,and it is extended to the variable step-size DOLMS algorithm.The theoretical analysis and the simulation results show that the proposed method has higher speed of convergence and less computational complexity than traditional block LMS algorithm.

Adaptive filter; Least Mean Square (LMS) algorithm; Direction optimization; Least Mean Square (LMS) ball; Direction Optimization Least Mean Square (DOLMS) algorithm

TN911.72

A

1009-5896(2014)06-1348-07

10.3724/SP.J.1146.2013.01038

王永 yongwang@ustc.edu.cn

2013-07-16收到，2014-01-17改回

国家863计划项目(2011AA7034056C)资助课题