Two-phase air-water flows: Scale effects in physical modeling*
PFISTER Michael
Ecole Polytechnique Fédérale de Lausanne (EPFL), Laboratory of Hydraulic Constructions (LCH), Station 18, CH-1015 Lausanne, Switzerland, E-mail: michael.pfister@epfl.ch
CHANSON Hubert
The University of Queensland, School of Civil Engineering, Brisbane QLD 4072, Australia
Two-phase air-water flows: Scale effects in physical modeling*
PFISTER Michael
Ecole Polytechnique Fédérale de Lausanne (EPFL), Laboratory of Hydraulic Constructions (LCH), Station 18, CH-1015 Lausanne, Switzerland, E-mail: michael.pfister@epfl.ch
CHANSON Hubert
The University of Queensland, School of Civil Engineering, Brisbane QLD 4072, Australia
(Received February 25, 2014, Revised April 8, 2014)
Physical modeling represents probably the oldest design tool in hydraulic engineering together with analytical approaches. In free surface flows, the similitude based upon a Froude similarity allows for a correct representation of the dominant forces, namely gravity and inertia. As a result fluid flow properties such as the capillary forces and the viscous forces might be incorrectly reproduced, affecting the air entrainment and transport capacity of a high-speed model flow. Small physical models operating under a Froude similitude systematically underestimate the air entrainment rate and air-water interfacial properties. To limit scale effects, minimal values of Reynolds or Weber number have to be respected. The present article summarizes the physical background of such limitations and their combination in terms of the Morton number. Based upon a literature review, the existing limits are presented and discussed, resulting in a series of more conservative recommendations in terms of air concentration scaling. For other air-water flow parameters, the selection of the criteria to assess scale effects is critical because some parameters (e.g., bubble sizes, turbulent scales) can be affected by scale effects, even in relatively large laboratory models.
air entrainment, hydraulic structures, physical modeling, scale effects, two-phase flow, Morton number
Introduction
In 1941, the tunnel spillway on the Arizona side of the Boulder Dam (USA) operated during four months with a relatively small discharge, when a routine inspection indicated that a 35 m long tunnel section was completely destroyed as a consequence of cavitation damage. The repairs included a re-lining combined with the installation of – then not yet common–aeration devices, and the US Bureau of Reclamation undertook a number of “air injection” device model studies in a 60:1 scale model[1]. This study certainly represented a pioneer work in chute aeration studies, although the results seemed rather disappointing at the time. Bradley[1]concluded: “The results of this investigation were negative in character. The plan for aeration of the Boulder Dam spillway by devices constructed on the tunnel invert…does not appear encouraging”. The statement reflected that only very small, insufficient air contents were measured in the physical model, designed based upon a Froude similitude. Bradley[1]acknowledged, “The viscosity of the water and air are same in both model and prototype, and that entrainment of air from the surface will be much more pronounced in the prototype”.
Air-water two-phase flows have been observed in several hydraulic structures, such as hydraulic jumps, intakes, drop-shafts, spillways, jets and plunge pools (Fig.1(a)). The flow phenomena in these structures are challenging, and yet relevant to hydraulic design. Physical model testing is often applied to investigate the related flow characteristics. In order to keep the physical models within economic dimensions and to minimize the discharges to supply, the Froude similitude and scale factors larger than 30:1 are often applied. These small models characteristically underestimate the air entrainment and transport in the fluid, because the effects of surface tension and viscosity are relatively over-represented in the model, given that water is used as fluid in both model and prototype. This is illustrated in Fig.1, showing a prototype operation (Fig.1(a)), two scale models at 10:1 and 25:1 geometric scales (Figs.1(b), 1(c)).

Fig.1 Comparison of air-water flows between prototype and laboratory model operations of stepped spillways, (a) Paradise dam stepped spillway (Australia) on 5 March 2013 (Photograph H. Chanson), Q≈2500 m3/s , hc/h=2.9, Re=7× 106, h= 0.62 m, θ=57o, (b) Laboratory experiments (Courtesy of Mr P. Royet, IFSTTAR) Q =0.40 m3/s , hc/h=3.2, Re=2.6× 105, h=0.06 m, θ=53o, and (c) Laboratory experiments (Courtesy of Mr P. Royet, IFSTTAR) Re<4×104, h=0.024 m, θ=63.4o, 59oand 53o(from left to right)
The literature describes mainly two approaches to combine the Froude similitude with a reasonable approximation of the rate of air entrainment, namely (a) limit the model scale to maximally 10:1[2,3], or (b) respect minimum values of the Weber or Reynolds numbers[4]. Both approaches allow more realistic predictions of air entrainment and transport based upon the scaled model results. These limits are derived from model families or comparisons with prototype measurements, if available[5].
Early studies of the bubble rise velocity in stagnant fluids highlighted the relevant dimensionless numbers, namely the Reynolds and Weber numbers. The results suggested some limiting value of them, above which the effect of fluid constants on the bubble motion is small. In these contributions, the introduction of the Morton number[6], as a link between the aforementioned numbers, allows for an expression of these limiting values as function of the Froude number. This concept is applied to free-surface flows in hydraulic structures on the basis of recent scaling limitations, and the notion of scale effects is discussed in a broader context.
1. Bubble rise velocity in stagnant fluid
The motion of a rising bubble in a stagnant fluid is dominated by the physical constants of the fluid and of the gas, namely μ is the dynamic viscosity, ρ is the density and σ is the surface tension. The first two variables must be theoretically considered for both gas and fluid phases. For pressures which are far from the critical point, the forces within a gas bubble might be neglected as they are small compared to those within the liquid. Note that the critical point describes the condition at which the phase boundary between fluid and gas terminates. For water, the latter is at around 374oC and 22 MPa. These conditions are unlikely in hydraulic engineering, and the gas (herein air) properties are of minor significance.
The motion of gas bubbles in a fluid is governed by buoyancy, resulting from the density difference between gas and fluid. If the gas density is negligible in comparison to that of the fluid, as for air and water, the buoyancy is a function of the pressure gradient∂P/∂z, hence the gravitational acceleration g, where z is the vertical elevation. Buoyancy depends further upon the bubble volume which is typically linked to an equivalent sphere diameter D. When a bubble moves relative to the surrounding fluid, the latter generates a resistance linked to the bubble (subscript b) rise velocity Vb.
Schmidt[7]conducted a dimensional analysis of the bubble motion in fluids. He concluded that the related processes can be described based on the following dimensionless numbers:
The bubble Reynolds number

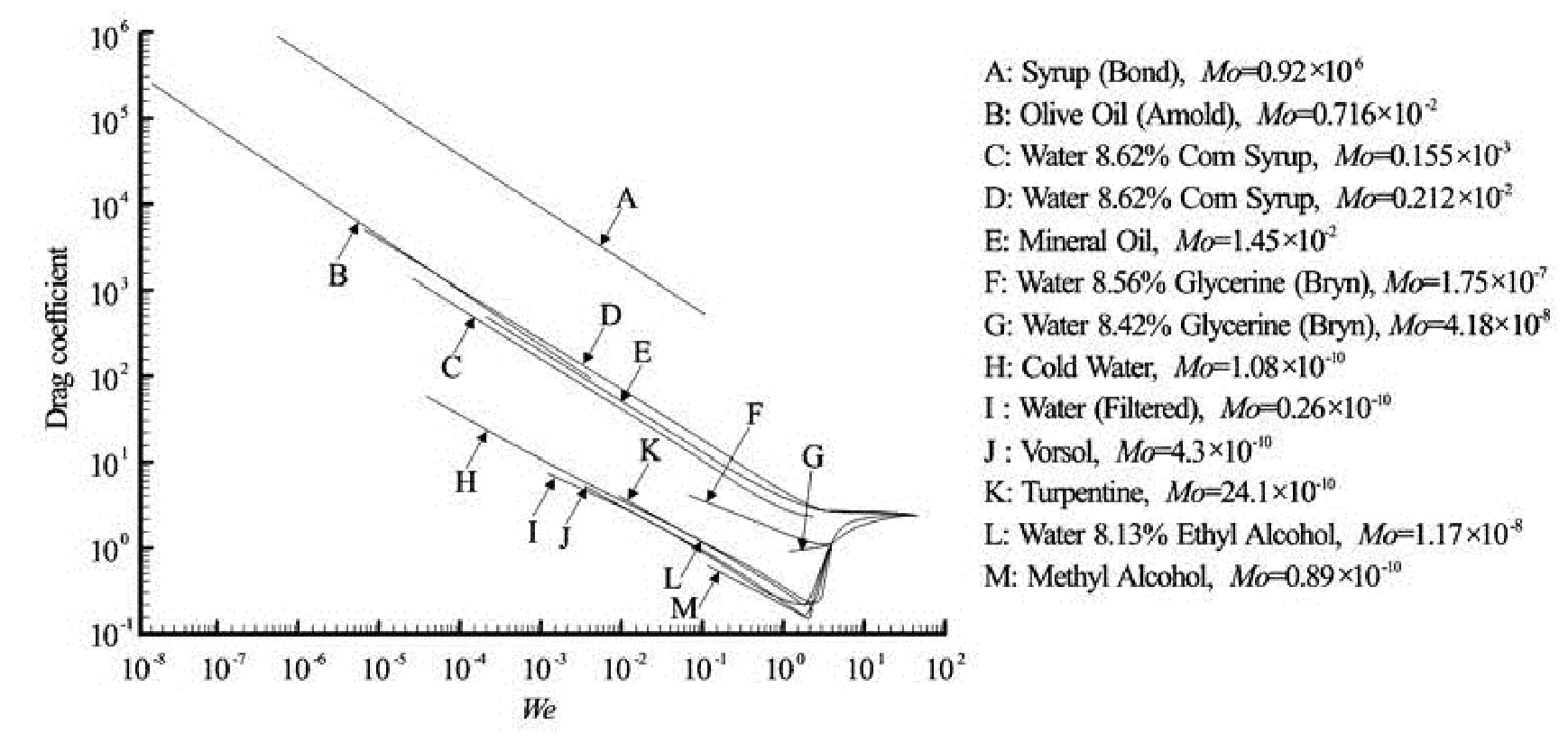
Fig.2 Drag coefficient as a function of the bubble Weber number Webfor a single bubble rising at terminal velocity in various stagnant fluids (Habermann and Morton 1954)
The bubble Froude number

where ν=/μ σ is the kinematic viscosity. The bubble rise velocity Vbwas included in all dimensionless numbers, and it could not be derived simply from dimensionless charts based upon Reb, Frband Web. A rearrangement was thus proposed to give only one explicit term containing Vb, namely that of the bubble Reynolds number Reb. Schmidt suggested
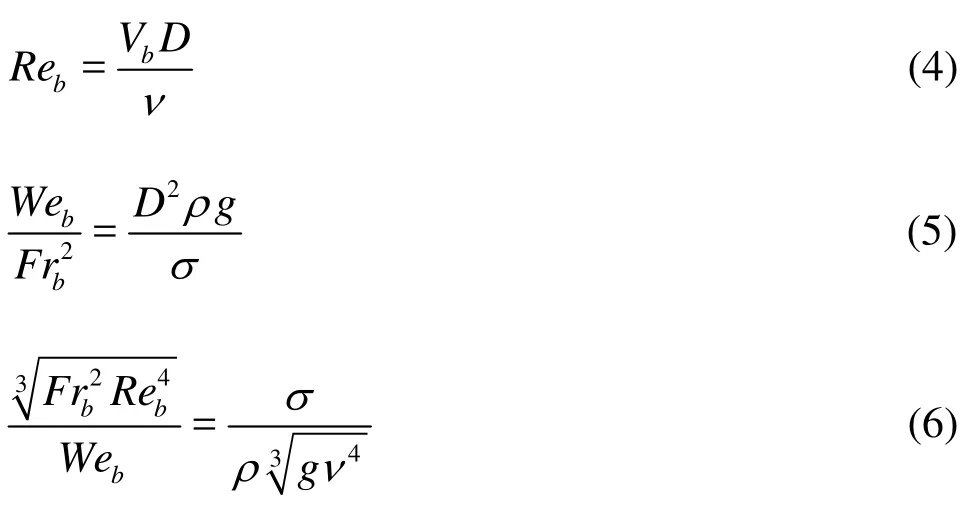
Equation (4) describes a priori the bubble characteristics including its diameter D and rise velocity Vb. Equation (5) includes the bubble diameter, fluid constants and gravity acceleration, while Eq.(6) contains exclusively the fluid constants and gravity acceleration. Consequently the bubble rise velocity in a stagnant, infinite fluid volume was expressed by Schmidt[7]as
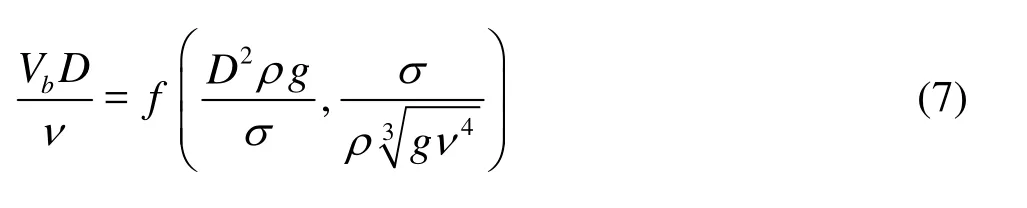
He concluded that physical experiments had to be conducted to support the above hypotheses, in particular with different fluids.
Habermann and Morton[8]performed some experiments related to the drag coefficient of freely rising air bubbles in stagnant fluids under various fluid properties: water at 6oC, 19oC, 21oC and 49oC, glim solution, mineral oil, varsol, turpentine, methyl alcohol, olive oil, syrup, different corn syrup-water mixtures, glycerin-water mixtures, and an ethyl alcohol-water mixture. Equation (6) was adapted by introducing the dimensionless parameter Mo=gμ4/(ρσ3), now called the Morton number[6]

The tests of Habermann and Morton[8]covered 0.2× 10-2≤Mo ≤0.3× 10-11.
With increasing bubble size, a change in rising bubble shape was observed, from spherical to ellipsoidal, and finally to spherical cap, for all liquids[8,9]. The bubble volumes at which the transition occurred were functions of the fluid properties, thus of the dimensionless number Mo. The reasoning may be applied to similar bubbles in different fluids, as well as for a single fluid including bubbles under different scale factors. The latter is a common situation in physical modeling of high-velocity free-surface flows in hydraulic structures. There, the two-phase gas-liquid flows are characterized by constant properties since air andwater are used in both prototype and model, whereas other characteristic values linked to geometry and force ratios may vary. Note however that Habermann and Morton[8]concluded that the air bubble motion at the terminal velocity cannot be described solely by the dimensionless numbers presented in Eqs.(4) to (6), because the drag coefficient was also a function of the gas phase motion within the bubbles.
An example for the effect of the Morton number Mo on the rise bubble drag coefficient is shown in Fig.2. Although no clear trend is recognizable, “large” values of Mo(10-2) tended to relatively large drag coefficients, whereas “small” values of Mo(10-11) indicate smaller drag coefficients. Interestingly, for Web>40, all drag coefficient curves tended to collapse, independent of Mo. A similar trend could be seen in terms of the bubble Reynolds number Reb, where the data collapsed for Reb>3×103. The latter would imply that the terminal bubble rise velocity of air bubbles is similar when the equivalent bubble diameter is larger than some 0.01 m to 0.02 m. In practice, the air bubble rise velocity in water tends to be constant for bubble diameters between 0.001 m and 0.02 m, with increasing rise velocity with augmenting bubble size for D>0.02 m[9].
2. Conceptual analogy to air-water mixture-flow
In physical modeling of hydraulic structures, the behavior of a single air bubble in stagnant water is rarely of interest. Typically, the studies focus on the characteristics of air-water mixture flows as a continuum medium, for example, in stepped spillways, hydraulic jumps, free water jets, steep chutes, and dropshafts. The knowledge of the air bubble entrainment and transport is essential to describe the flow properties, including the adequate free-board height, jet disintegration, friction losses, and air-water mass transfer rate[2,10,11].
Most physical models are kept within economical dimensions, implying a Froude similitude with a geometric scale ratio of typically 30:1 to 60:1[12,13]. The dynamic similitude used to derive model-scaling laws considers the ratios of forces acting on the fluid(s)[6]. The ratio of inertia to gravity forces results in the Froude number; the ratio of inertia to viscous forces gives the Reynolds number, the ratio of inertia to surface tension forces yields the Weber number. A true dynamic similarity of aerated flows require achieving identical Froude number, Reynolds number and Weber number in both prototype and model. This is physically impossible when the same fluids (air, water) are used in both prototype and model[6]. As a consequence, small scale models based upon the Froude similitude may underestimate the air transport in the fluid, because the relative effects of surface tension and viscosity are over-represented[11,14]. Since a true dynamic similitude exists only at full-scale, the underestimation of scale model air entrainment and transport must be minimized in modeling practice by limitations in terms of We or Re. These limits are derived from systematic model families and comparisons with prototype data.

Fig.3 Bottom air concentration Cbcurves versus normalization functions f, downstream of (a) deflector, (b) drop aerators, with trend line for unaffected tests (–) and symbols for tests affected by scale effects, (–) Pfister and Hager (2010b) with data We0.5>140
Such limits represent a link between the above description related to the bubble rise velocity (Section 1) and observations from model families (Section 3). By following the results for single bubbles in a stagnant fluid[7,8], a similar concept is proposed herein to adequately model an air-water mixture-flow continuum under a reduced geometric scale factor. The relevant dimensional numbers are:
The Reynolds number

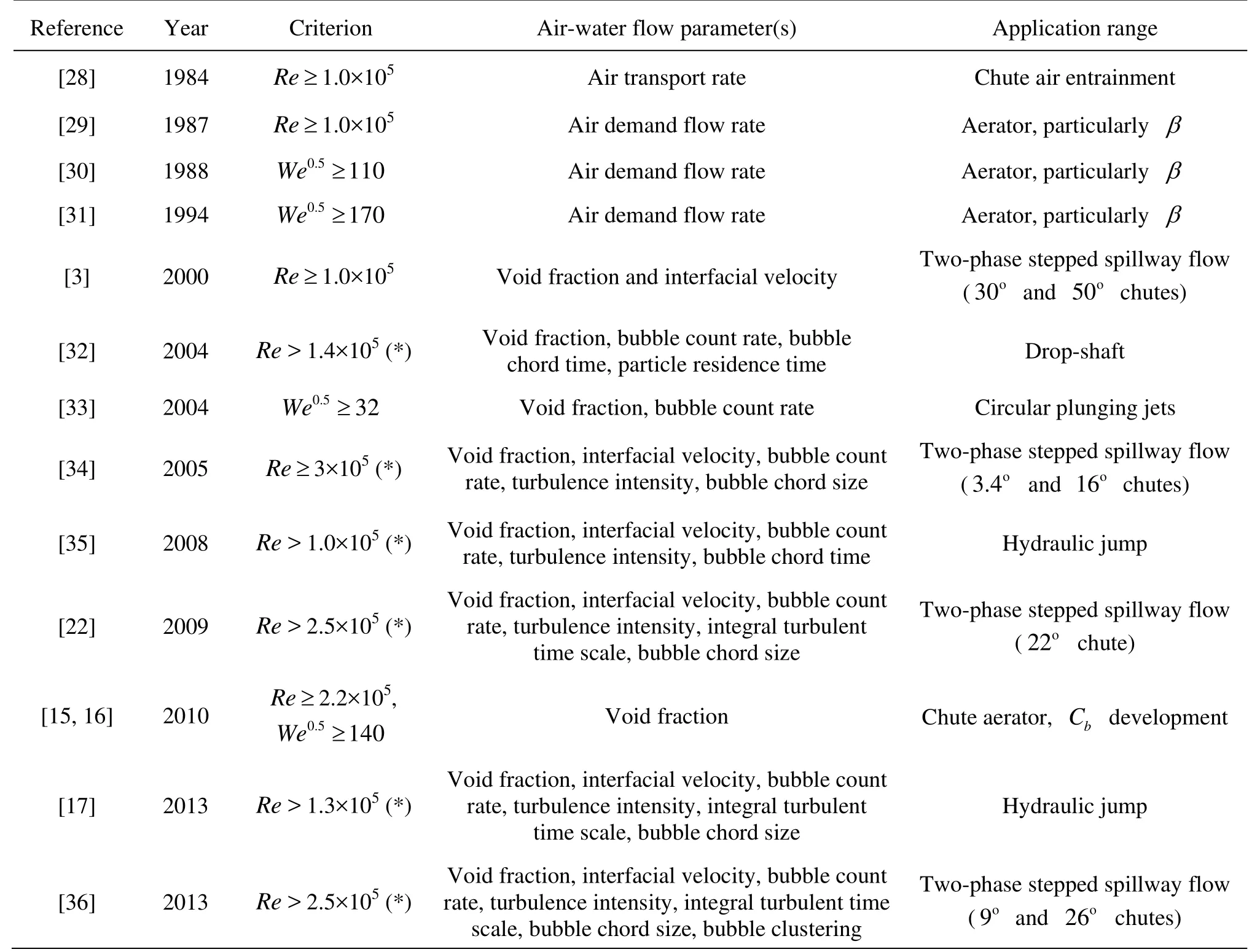
Table 1 Limiting scale factors to prevent significant scale effects in two-phase air-water flows under Froude similitude, with a focus on air concentrations (also denoted as void fraction) for undistorted air-water scale models
The Weber number


3. Limiting factors
A number of model families and comprehensive data sets were published to test scale effects in the modeling of air-water two-phase flows. These studies were based upon the Froude and Morton similitudes with undistorted models in geometrically similar models under controlled flow conditions to assess the associated-scale effects. Table 1 summarizes a number of relevant studies, leading to some suggested limiting criteria of about We0.5>110 to 170 and Re>1×105to 3×105when the relevant scaling parameter is the air concentration. For example, Pfister and Hager[15,16]identified a gross underestimate in terms of local bottom air concentration by up to one magnitude as We0.5<140. This is illustrated in Fig.3, where the abscissa corresponds to the streamwise normalizations fDand fSgiven by these authors, and the trend lines correspond to the best fit of all data from tests with We0.5≥140.
Despite the relatively limited scope of experimental investigations listed in Table 1, their results demonstrated unequivocally the limitations for the physical modeling of two-phase air-water flows. The findings of these systematic experimental studies highlighted that (1) the notion of scale effects must be defined in terms of some specific set of two-phase airwater characteristics, and (2) some aerated flow properties are more affected by scale effects than others, even in large-size facilities[5,14]. The selection of the criteria to assess scale effects is critical: e.g., void fraction, turbulence intensity, or bubble size. Any mention of scale effects must be associated with a list oftested parameters[14,17], and this is well-known in mono-phase flows[18]. The experimental data showed that some parameters, such as bubble sizes and turbulent scales, are likely to be most affected by scale effects[5,14,19]. It is noteworthy that no distorted physical modeling of air-water flows was considered yet, though the scale distortion may enable to achieve some similarity in terms of bubble rise velocity on chute spillways and inclined plunging jets.
Self-similarity is another powerful tool in turbulent air-water flow investigations involving a wide spectrum of spatial and temporal scales. Self-similarity is closely linked to dynamic and kinematic similarities, and the existence of self-similar relationships may have major implications on the measurement strategy in experimental and physical modeling studies[20,21]. Although it is impossible to achieve a true dynamic similarity in air-water flows because of too many relevant dimensionless parameters, a number of laboratory data showed several self-similar relationships that remain invariant under changes of scale. The results may provide a picture general enough to be used, as a first approximation, to characterize the air-water flow properties in similar hydraulic structures irrespective of the physical scale[22].
In addition to dynamic similarity and self-similarity, a further modeling approach may be based upon some theoretical developments leading to theoretically-based equations. An illustration is the analytical solution of the advection diffusion equation for air bubbles[2,11,23,24]. The existence of theoretical relationships may have some implications regarding the laboratory study approach and measurement methods. The existence of an analytical solution may allow a drastic reduction of the amount of measurements.
4. Discussion
Previous studies used mostly two criteria to assess scale effects, i.e., the limiting values in terms of We0.5and Re (Table 1). When the same fluids (air and water) are used in prototype and model, the two numbers depend on each other, besides Fr and the Morton number Mo (Eq.(8)). The use of the Froude similitude with air and water as fluids in both model and the prototype leads to a similitude in terms of the Morton number: Mo is the constant and Fr is the constant. For a given Froude number Fr, the product MoFr2=We3/Re4has to be identical in the model and prototype flows. A transformation of Eq.(8) gives the direct relationship between the Reynolds number and Weber number


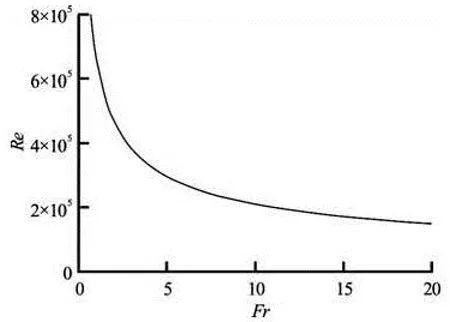
Fig.4 Relationship between Re and Fr for We0.5=140 (Eq.(12))
Table 1 suggests that the proposed limiting relationships in terms of scale effects for air-water flows have become more restrictive over time. The trend might be linked to the development in measurement techniques, allowing for more precise and punctual (instead of cross-sectional) two-phase air-water flow measurements. Ultimately, no scale effect is observed at full scale only, using air and water in prototype and model: i.e., in prototype flow conditions. But prototype observations are rare. The Aviemore Dam spillway investigations in New Zealand remain a key reference[25,26]. A few prototype observations were conducted, mostly qualitative like at the Dachaoshan Dam spillway[27]. But even the Aviemore Dam spillway data sets might be challenging. The flow conditions corresponded to Re≈2×106, which is one to two orders of magnitude lower than the design flow conditions of very large spillway systems. A number of recent air-water studies on dynamic similarity would suggest that the extrapolation of Aviemore Dam results could be subjected to some scale effects at larger Reynolds number. Figures 1 and 5 provide some comparative illustrations of prototype and laboratory airwater two-phase flows. Figure 1 presents some airwater skimming flow above a stepped spillway. The close-up photographs suggest that the turbulence next to the inception point of free-surface aeration differs significantly between prototype and models for a com-parable Froude number. Figure 5 shows a hydraulic jump stilling basin in operation. In the prototype (Fig.5(a)), the hydraulic power dissipated in the hydraulic jump as 6 MW per unit width, compared to 230 W/m in the laboratory model (Fig.5(b)) for an identical Froude number. Again the surface turbulence appears substantially different despite an identical Froude number.

Fig.5 Comparison of air-water flow features between prototype and laboratory model operations of hydraulic jumps, (a) Hydraulic jump stilling basin downstream of Paradise Dam spillway (Australia) on 30 December 2010 (Courtesy of B. Chanson): Q≈6 300 m3/s, Fr=8, Re=2×107, and (b) Laboratory experiment: Q=0.030 m3/s, Fr=8, Re=6×104
5. Conclusions
The physical modeling of air-water two-phase flows in hydraulic engineering would require the Froude number (Fr), Weber number (We) and Reynolds number (Re) to be identical in prototype and laboratory. This is physically impossible unless working at full-scale. A re-arrangement of the dimensionless numbers results in the introduction of the Morton number (Mo). The survey of a number of detailed investigations served as the basis to the described scale effects in modeling high-speed two-phase flows. The results have highlighted the significance of the non-dimensional numbers Fr, We and Re, their combination yielding Mo, and some limiting values of Re or We to reduce scale effects. Combining these considerations together with published limits to minimize scale effects in terms of air concentration, the outcome indicates that values of Re>2×105to 3× 105should be respected to avoid relevant scale effects in terms of air concentrations within 5≤Fr≤15. If one limitation is considered, then the other is implicitly respected. For Fr<5, these limits have to be selected more conservatively. The notion of scale effects is closely linked with the definition of specific set of two-phase air-water characteristics.
The results of recent experimental investigations emphasized that the selection of the criteria to assess scale effects is critical. These results show that some parameters, such as bubble sizes and turbulent scales, are likely to be affected by scale effects, even in relatively large-size laboratory models (e.g., 2:1 to 3:1). No scale effect is only observed at full scale using the same fluids in prototype and model. As final words, the present study emphasizes (again) the needs for full-scale prototype data of two-phase air-water flows, typically observed in prototype hydraulic structures.
Acknowledgement
The work was supported by the Australian Research Council (Grant No. DP120100481).
[1] BRADLEY J. N. Study of air injection into the flow in the boulder dam spillway tunnels[R]. Hydraulic Labora- tory Report 186, USBR, Denver CO., 1945.
[2] CHANSON H.Air bubble entrainment in free-surface turbulent shear flows[M]. London, UK: Academic Press, 1997.
[3] BOES R. M. (MINOR H. E., HAGER W. H. eds.).Scale effects in modelling two-phase stepped spillway flow (Hydraulics of stepped spillways)[M]. Rotterdam, The Netherlands: A. A. Balkema, 2000, 53- 60.
[4] PFISTER M., CHANSON H. Discussion to scale effects in physical hydraulic engineering models[J].Jour-nal of Hydraulic Research,2012, 50(2): 244-246.
[5] CHANSON H. Hydraulics of aerated flows: Qui Pro Quo?[J].Journal of Hydraulic Research,2013, 51(3): 223-243.
[6] PFISTER M., HAGER W. H. History and significance of the Morton number in hydraulic engineering[J].Journal of Hydraulic Engineering,2014, 140(5): 02514001.
[7] SCHMIDT E. Ähnlichkeitstheorie der Bewegung von Flüssigkeitsgasgemsichen (similarity theory of motion in fluid-gas mixtures)[R]. Forschungsheft 365, 1-3, VDI- Verlag, Berlin, 1934(in German).
[8] HABERMAN W. L., MORTON R. K. An experimental study on bubbles moving in liquids[J].Transactions of the American Society of Civil Engineers,1956, 121(1): 227-250.
[9] COMOLET R. Sur le mouvement d’une bulle de gaz dans un liquide (gas bubble motion in a liquid medium)[J].La Houille Blanche,1979, (1): 31-42(in French).
[10] RAO N. S. L., KOBUS H. E. and BARCZEWSKI B. H.Characteristics of self-aerated free-surface flows[M]. Berlin, Germany: E. Schmidt Verlag, 1975.
[11] WOOD I. R.Air entrainment in free-surface flows. IAHR hydraulic structures design manual 4[M]. Rotterdam, The Netherlands: A. A. Balkema, 1991.
[12] NOVAK P., CABELKA J.Models in hydraulic engineering. physical principles and design applicatio-ns[M]. London, UK: Pitman Publication, 1981.
[13] CHANSON H. (CHANSON H. eds.)Physical modelling of hydraulics (Hydraulics of open channel flow: An introduction)[M]. 1st edition, London, UK: Edward Arnold, 1999, 261-283.
[14] CHANSON H. Turbulent air-water flows in hydraulic structures: Dynamic similarity and scale effects[J].En-vironmental Fluid Mechanics,2009, 9(2): 125-142.
[15] PFISTER M., HAGER W. H. Chute aerators I: Air transport characteristics[J].Journal of Hydraulic Enginee-ring, ASCE,2010, 136(6): 352-359.
[16] PFISTER M., HAGER W. H. Chute aerators II: Hydraulic design[J].Journal of Hydraulic Engineering,ASCE,2010, 136(6): 360-367.
[17] CHANSON H., CHACHEREAU Y. Scale effects affecting two-phase flow properties in hydraulic jump with small inflow Froude number[J].Experimental The-rmal and Fluid Science,2013, 45: 234-242.
[18] SCHULTZ M. P., FLACK K. A. Reynolds-number scaling of turbulent channel flow[J].Physics of Fluids,2013, 25(2): 025104.
[19] CHANSON H.Environmental hydraulics of open channel flows[M]. Oxford, UK: Elsevier Butterworth- Heinemann, 2004, 483.
[20] BARENBLATT G. I.Scaling, self-similarity, and intermediate asymptotics[M]. Cambridge, UK: Cambridge University Press, 1996, 386.
[21] FOSS J., PANTON R. and YARIN A. (TROPEA C., YARIN A. and FOSS J. eds.).Nondimensional representation of the boundary-value problem (Experimental fluid mechanics)[M]. Berlin, Germany: Springer, 2007, 33-83.
[22] FELDER S., CHANSON H. Turbulence, dynamic similarity and scale effects in high-velocity free-surface flows above a stepped chute[J].Experiments in Fluids,2009, 47(1): 1-18.
[23] WOOD I. R. Air entrainment in high speed flows[C].Proceedings International Symposium Scale Effects in Modelling Hydraulic Structures, IAHR.Esslingen, Germany, 1984.
[24] CHANSON H. (GUALTIERI C., MIHAILOVIC D. T. eds.).Advective diffusion of air bubbles in turbulent water flows (Fluid mechanics of environmental interfaces)[M]. Leiden, The Netherlands: Taylor and Francis, 2008, 163-196.
[25] KELLER R. J. Field measurement of self-aerated high speed open channel flow[D]. Doctoral Thesis, Christ- church, New Zealand: University of Canterbury, 1972.
[26] CAIN P. Measurements within self-aerated flow on a large spillway[D]. Doctoral Thesis, Christchurch, New Zealand: University of Canterbury, 1978.
[27] LIN K., HAN L. Stepped spillway for dachaoshan RCC dam[C].Proceedings 29th IAHR Biennial Congress,Special Seminar.Beijing, China, 2001, 88-93.
[28] KOBUS H. (KOBUS H. ed.).Local air entrainment and detrainment (Symp. scale effects in modelling hydraulic structures)[M]. Esslingen: Technische Akademie, 1984, 1-10.
[29] KOSCHITZKY H.-P. Dimensionierungskonzept für Sohlbelüfter in Schussrinnen zur Vermeidung von Kavitationsschäden (Design concept for chute aerators to avoid cavitation damage)[R]. Mitteilung 65. Institut für Wasserbau, TU: Stuttgart, 1987(in German).
[30] RUTSCHMANN P. (VISCHER D. ed.).Belüftungseinbauten in Schussrinnen (Chute aerators) (Mitteilung 97. laboratory of hydraulics, hydrology and glaciolo-gy)[M]. ETH: Zurich, 1988(in German).
[31] SKRIPALLE J. Zwangsbelüftung von Hochgeschwindigkeitsströmungen an zurückspringenden Stufen im Wasserbau (forced aeration of high-speed flows at chute aerators)[R]. Mitteilung 124. Technische Universität, Berlin, 1994(in German).
[32] CHANSON H. Understanding air-water mass transfer in rectangular dropshafts[J].Journal of EnvironmentalEngineering and Science,2004, 3(5): 319-330.
[33] CHANSON H., AOKI S. and HOQUE A. Physical modelling and similitude of air bubble entrainment at vertical circular plunging jets[J].Chemical EngineeringScience,2004, 59(4): 747-754.
[34] CHANSON H., GONZALEZ C. A. Physical modelling and scale effects of air-water flows on stepped spillways[J].Journal of Zhejiang University Science,2005, 6A(3): 243-250.
[35] MURZYN F., CHANSON H. Experimental assessment of scale effects affecting two-phase flow properties in hydraulic jumps[J].Experiments in Fluids,2008, 45(3): 513-521.
[36] FELDER S. Air-water flow properties on stepped spillways for embankment dams: Aeration, energy dissipation and turbulence on uniform, non-uniform and pooled stepped chutes[D]. D octoral Thesis, Brisbane, Australia: The University ofQueensland, 2013.
10.1016/S1001-6058(14)60032-9
* Biography: PFISTER Michael (1976-), Male, Ph. D., Research and Teaching Associate
- 水动力学研究与进展 B辑的其它文章
- Effect of compressive stress on the dispersion relation of the flexural–gravity waves in a two-layer fluid with a uniform current*
- Coupled hydroelastic vibrations of an elliptical cylindrical tank with an elastic bottom*
- Experimental investigations of transient pressure variations in a high head model Francis turbine during start-up and shutdown*
- Improved conservative level set method for free surface flow simulation*
- Capillary effect on the sloshing of a fluid in a rectangular tank submitted to sinusoidal vertical dynamical excitation*
- Comprehensive analysis on the sediment siltation in the upper reach of the deepwater navigation channel in the Yangtze Estuary*

