一类含有2n个非零元的极小谱任意符号模式

李亚静，邵燕灵

(中北大学理学院，山西太原 030051)

一类含有2n个非零元的极小谱任意符号模式

李亚静，邵燕灵

(中北大学理学院，山西太原 030051)

设A为n阶符号模式，如果对任意n次首1实系数多项式r(x)，在符号模式A的定性矩阵类Q(A)中都有一个实矩阵B，且f(x)=r(x)为B的特征多项式，则称A是谱任意的.如果A的真子模式都不是谱任意的并且A是谱任意的，则称A为极小谱任意的.本文运用幂零-雅可比方法证明了一类新的含有2n个非零元的n阶符号模式为极小谱任意模式.

符号模式；蕴含幂零；谱任意；极小谱任意；幂零-雅可比方法

1 预备知识

符号模式矩阵的研究是组合数学研究领域中一个重要的分支.它被广泛地应用在计算机科学、经济学、物理、化学、社会学等很多学科中.文献[1]介绍了符号模式矩阵这一研究领域目前的部分基本定义及定理.文献[2]给出了谱任意符号模式的定义,并提出了幂零-雅可比方法来证明谱任意.之后的文献[3-8]分别给出了一些n阶的极小谱任意符号模式.下面先介绍一些相关概念.

定义1[1]符号模式矩阵是元素取自集合{1,-1,0}的矩阵.若A=(aij)是给定的实矩阵，则A的符号模式矩阵是由aij的符号所确定的矩阵，记为sgn(A).符号模式矩阵A=(aij)的定性矩阵类为Q(A)={B=(bij)|sgn(bij)=aij,i,j=1,2,…，n}

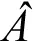
定义3[1]对于符号模式矩阵A，A蕴含幂零指的是存在正整数k和一个实矩阵B∈Q(A)，使得Bk=0，Bk-1≠0，其中幂零矩阵为B，幂零矩阵B的指数为k.

定义4 设A为n阶符号模式，如果任意的实矩阵B∈Q(A)是(非)奇异的，则称A是符号(非)奇异的.

定义5[2]设A为n阶符号模式，f(λ)为任意的n次首1实系数多项式，若对于f(λ)都存在实矩阵B∈Q(A)，使得B的特征多项式为f(λ)，则符号模式矩阵A为谱任意的.

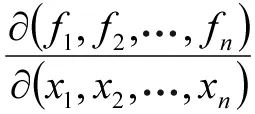
本文讨论一类n阶符号模式A=(aij)n×n(n≥5):

.

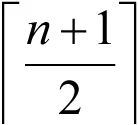
2 主要结果

定理1 当n≥5时，符号模式A及其所有的母模式都是谱任意的.

证明 任取实矩阵B∈Q(A),设B有如下形式：

其中a1<0,sgn(ai)=(-1)i-1(i=2,3,…,n-2),sgn(an-1)=(-1)n-r,sgn(an)=(-1)n.

设fB(λ)=det(λI-B)=λn+α1λn-1+…+αn-1λ+αn.则当r≥4时，

将行列式的第i行的λ倍加到第i-1行(i=n,n-1,…,2)得

将行列式第i行的-ai-1倍加到第1行(i=3,4,…,n)得

将行列式依次按第i列展开(i=2,3,…,n-2),得

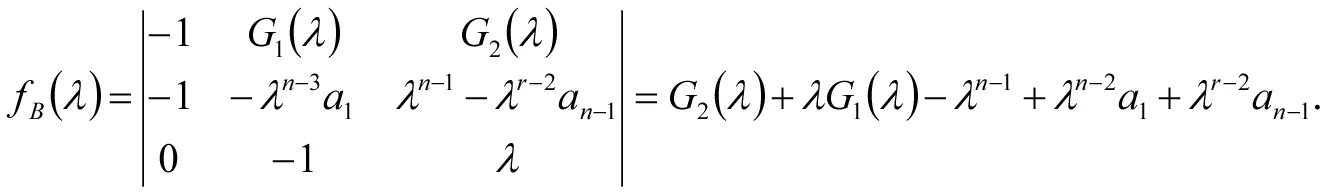
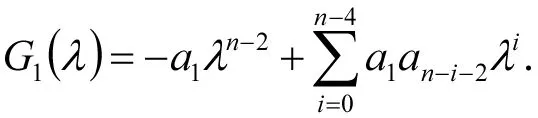
即

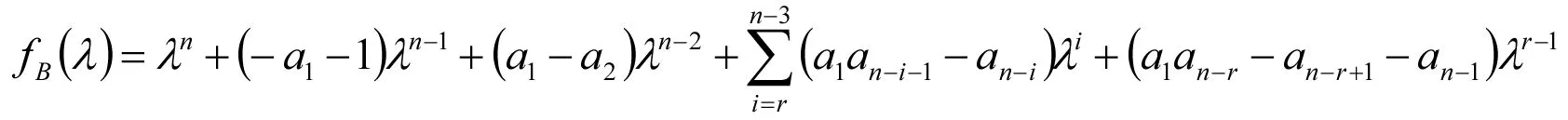
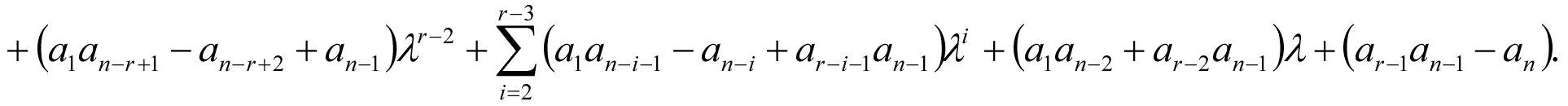
当r=2,3时，类似地可以计算出B的特征多项式.

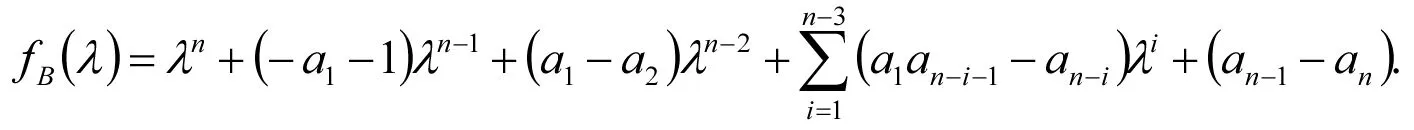
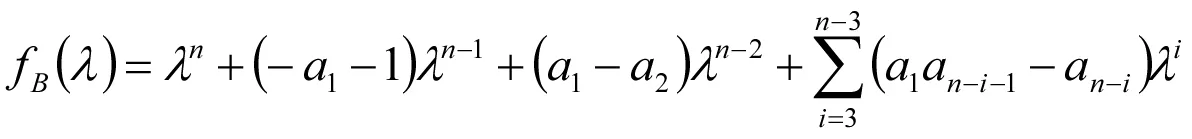
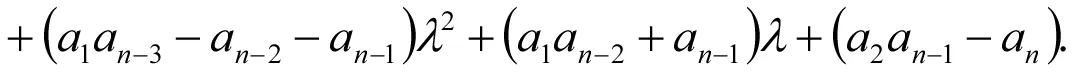
因此

α1=-a1-1，

α2=a1-a2，

αn-i=a1an-i-2-an-1(i=n-3，n-4，…，r+1，r)，

αn-r+1=α1αn-r-an-r+1-an-1，

αn-r+2=a1an-r+1-an-r+2+an-1，

αn-j=a1an-j-1-an-j+ar-j-1an-1(j=r-3，r-4，…，2)，

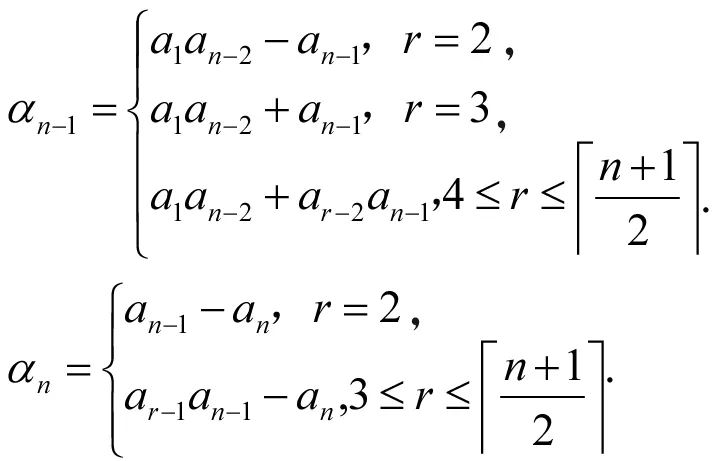
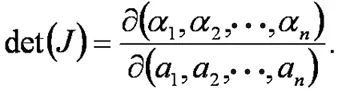
当r=2时，

(1)

当r=3时，

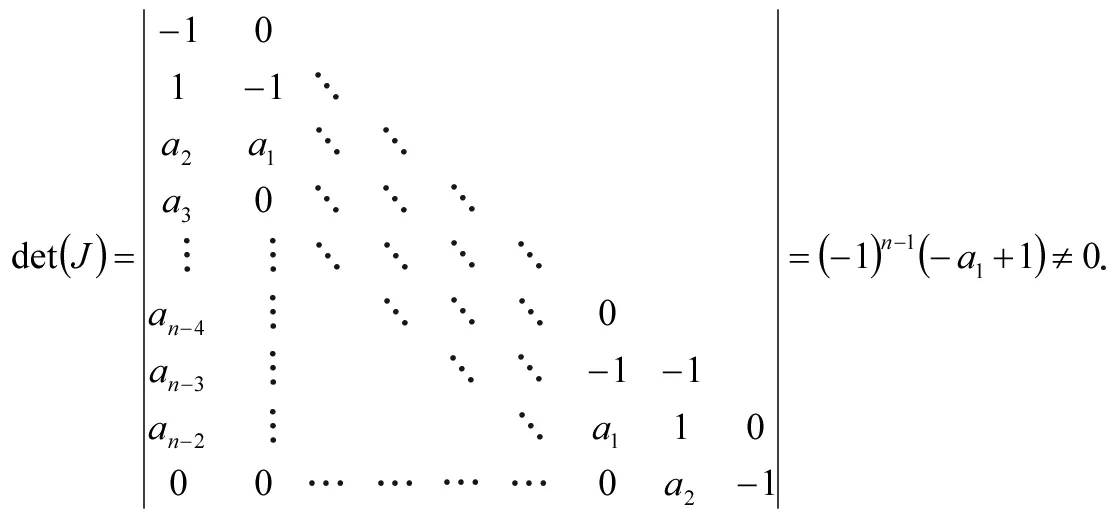
(2)

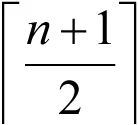
其中第n-1列的-1在第n-r+1行,第n-r+1行的另一个-1在第n-r+1列.

将行列式先按第n列展开，再依次按第1,2,…,n-r-1,n-r行展开，得

将行列式第i行的a1倍加到第i+1行(i=2,3,…,r-2)，得

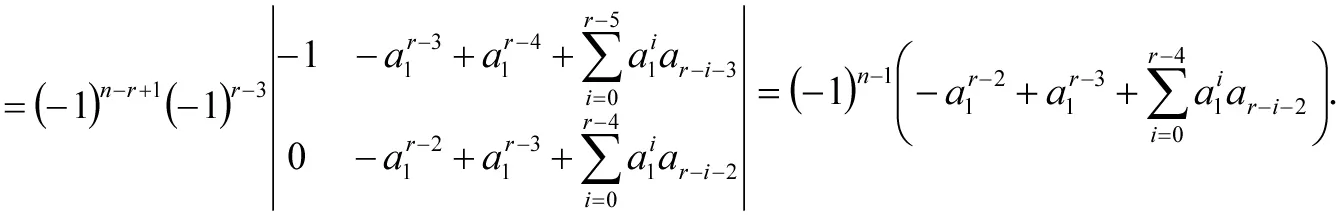
因为a1<1,sgn(ai)=(-1)i-1(i=2,3,…,n-2),

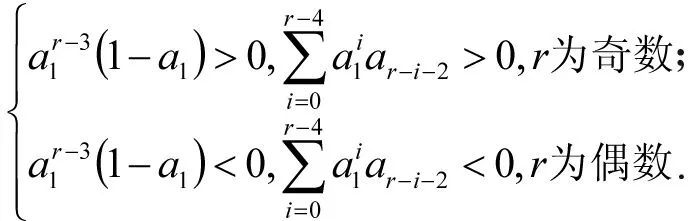
从而得到

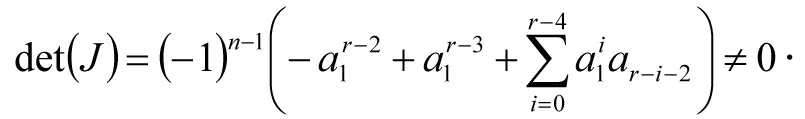
(3)

当ai=-1(i=1及2≤i≤n-r,i为偶数)，

aj=1(3≤j≤n-r,j为奇数)，

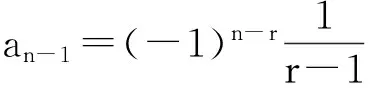
定理2 当n≥5时,符号模式A是极小谱任意的.

证明 设M=(mij)n×n是A的一个真子模式，且M是谱任意的，则(1)m11≠0,mn-1,n-1≠0,否则M的迹为负或为正,与M是谱任意模式矛盾；(2)mi,i-1≠0(i=2,3,…，r-1,r+1,…,n-2,n),否则M是符号奇异的,与M是谱任意模式矛盾；(3)mi,i-1≠0(i=r,n-1)，否则M是符号非奇异的,与M是谱任意模式矛盾；(4)m1,i≠0(i=2,3,…，n-2,n),mr,n≠0，否则ai=0(i=2,3,…,n)，与M是谱任意模式矛盾.

综合上面讨论可知A是极小谱任意的.

[1]Leslie Hogben.Handbook of linear algebra[M].Bocaraton:CRC Press,2007.

[2]Drew J H,Johnson C R, Olesky D D,et al.Spectrally arbitrary patterns[J].Linear Algebra and Its Applications, 2000,308(1):121-137.

[3]Britz T, McDonald J J, Olesky D D, et al.Minimal spectrally arbitrary sign pattern[J].SIAM Journal on Matrix Analysis and Applications,2004,26(1):257-271.

[4]Cavers M S, Kim I J, Shader B L,et al.On determining minimal Spectrally arbitrary patterns[J].Elec. J. Linear Algebra,2005,13:240-248.

[5]Cavers M S,Vander Meulen K N.Spectrally and inertially arbitrary sign patterns[J].Linear Algebra and Its Applications,2005,394:53-72.

[6]GAO Yu-bin, SHAO Yan-ling. A spectrally arbitrary patterns[J].Advances in Mathematics,2006,35(5):551-555.

[7]R.Pereira.Nilpotent matrices and spectrally arbitrary sign-patterns[J].Electorn.J.Linear Algebra,2007,16:232-236.

[8]Bergsma H,Kevin N,Vander M,et al.Potentially nilpotent patterns and the Nilpotent-Jacobian method [J].Linear Algebra and Its Applications,2012(436):4433-4445.

A Class of Minimal Spectrally Arbitrary Sign Patterns with 2n Nonzero Entries

LI Ya-jing, SHAO Yan-ling

(School of Science, North University of China, Taiyuan Shanxi 030051, China)

Ais set up ofnsign pattern.Ais spectrally arbitrary if for every real polynomialr(x) of degreenthere exists a matrixB∈Q(A) that hasf(x)=r(x) as its characteristic polynomial. IfAis spectrally arbitrary , and no proper subpattern ofAis spectrally arbitrary , thenAis a minimal spectrally arbitrary sign pattern. In this paper, a new class of minimal spectrally arbitrary sign patternes of ordernwith 2nnonzreo entries is given by using the Nilpotent-Jacobian method.

Sign pattern; Potentially nilpotent; Spectrally arbitrary sign pattern; Minimal spectrally arbitrary sign pattern; Nilpotent-Jacobian method

2014-02-03

山西省回国留学人员科研资助项目(12-070)。

李亚静(1990- )，女，山西运城人，中北大学理学院硕士研究生，从事组合数学研究。

邵燕灵(1963- )，女，山西平定人，博士生导师，博士，从事组合数学研究。

O157

A

2095-7602(2014)04-0007-06