On J-clean Rings

HU Xiaomei， CHEN Huanyin

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

On J-clean Rings

HU Xiaomei， CHEN Huanyin

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

J-clean ring; extension of rings; Morita context; Jacobson radical

1 Introduction

Following the paper [1], Nicholson called a ringRis clean if every elementr∈Rcan be written in the form ofr=e+uforeis an idempotent anduis a unit. A nil clean ring was introduced by Diesl[2]and defined an elementrin a ringRto be nil clean ifr=e+wfore∈Id(R) andw∈N(R). Later, following Diesl[3], a ringRis strongly nil clean provided that for anyr∈Rthere exists an idempotente∈Rsuch thatr-e∈N(R) andre=er. On the other hand, J-clean rings are studied by Chen[4]. A ringRis called a J-clean ring if every elementr∈Rcan be written in the form ofr=e+jwhereeis an idempotent andjbelongs to Jacobson radical. If we add an additional condition thatej=jeon the above definition it is called a strongly J-clean ring. Now, we continue the study of J-clean rings. We will discuss various properties of the J-clean rings and these rings are equivalent to each other with some other conditions.

Throughoutthispaper, Id(R)denotesthesetofallidempotentsofR, J(R)denotestheJacobsonradicalofRandU(R)denotestheunitofR.

2 Equivalent Characterizations

Definition 1 A ringRis called a J-clean ring if every elementa∈Rcan be written in the form ofa=e+jwheree∈Id(R) andj∈J(R).

Proposition 1 Every homomorphic image of J-clean ring is J-clean.

Proof This is obvious.

Theorem 1 LetRbe a ring. ThenRis J-clean if and only if

1)Ris clean.

2)R/J(R) is Boolean.

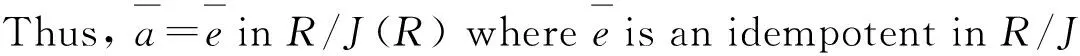
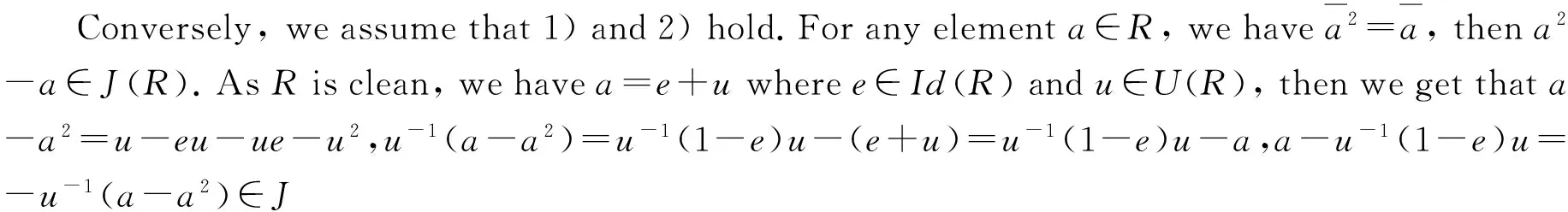
Every J-clean ring is clean ring, but the converse is not true as the following shows.

Example 1 Z3is a field, so Z3is clean. 0 and 1 are the only idempotents in Z3, and that 0 is the only elements in the Jacobson radical of Z3. We easily know that 2 can not be in the form ofe+jwheree∈Id(Z3) andj∈J(Z3), as a result, it is not J-clean but it is clean.

We note that the transpose of every invertible matrix over J-clean rings is also invertible. IfRis J-clean, thenR/J(R) is Boolean, hence, it is commutative, and we have done.

Theorem 2 LetRbe a ring. Then the following are equivalent:

1)Ris J-clean.

2)R[[x]] is J-clean.

Proof 1)⟹2). Suppose thatRis J-clean, for anya∈R, we havea=e+j. Thenf(x)=a0+a1x+a2x2+…=e+j+(a1x+a2x2+…)=e+(j+a1x+a2x2+…)=e+α(x). It is easy to knowα(x)∈J(R[[x]]), hence,R[[x]] is J-clean.

Corollary 1 LetRbe a ring.R[[x1,…,xn]] is J-clean if and only ifRis J-clean.

Proof By introduction and Theorem 2.

Proposition 2 LetRbe a J-clean ring. Then 2∈J(R).

Proof Clearly, there exist an idempotente∈Id(R) and aw∈J(R) such that 2=e+w. Hence, 1-e=w-1∈U(R), 1-e=1. Soe=0. As a result, 2=w∈J(R).

Proposition 3 LetRbe a ring. Then the following conditions are equivalent:

1)Ris Boolean.

2)Ris J-clean andJ(R)=0.

Proof 1)⟹2). Clearly,Ris J-clean. For anyx∈J(R),x=x2. Sox=0. This implies thatJ(R)=0.

2)⟹1). It is obvious.

Theorem 3 LetRMRbe an (R,R)-bimodule ring. Then the trivial extensionR∝Mis J-clean if and only ifRis J-clean.

Now we characterize when Znis J-clean. We recall that,Id(Zpk)={0,1} andJ(Zpk)=pZpk, for any primep∈N.

Lemma 1 Z2k,k∈N, is J-clean.

Proof Clearly,Id(Z2k)={0,1} andJ(Z2k)=2Z2k={0,2,4,…,2(2k-1-1)}. Hence, for anya∈Z2k, there existe∈Id(Zpk) andw∈J(Zpk) such thata=e+w. Sok∈N is J-clean.

Theorem 4 Zpk,k∈N, is J-clean wherepis prime ifp=2.

Proof (⟸). It follows from Lemma 1.

(⟹). Suppose Zpkis J-clean, then Zpk/J(Zpk) is Boolean by Theorem 1. As we know Zpk/J(Zpk)≅Zp, so Zpis Boolean. And Zpis a field, we get Zp≅Z2. Hence,p=2.

Corollary 2 Zpis J-clean ifp=2.

Theorem 5 LetRbe a local ring. Then the following are equivalent:

1)Ris J-clean.

2)R/J(R)≅Z2.

2)⟹1).SupposeR/J(R)≅Z2,thenforanya∈R, a=0+wora=1+wwherew∈J(R),soRisJ-clean.

Theorem 6 LetRbe a ring. ThenRis J-clean if and only if

1)Ris clean.

2)U(R)=1+J(R).

Proof SupposeRis J-clean,Ris clean by Theorem 1. Letu∈U(R), thenu=e+jwheree∈Id(R) andj∈J(R). Thene=u-j=u-(1+j)+1∈U(R). Hence,e=1. Sou=1+j, as desired.

Conversely, we assume that 1) and 2) hold. For any elementa+1∈R, we havea+1=e+uwheree∈Id(R) andu∈U(R). SinceU(R)=1+J(R),a+1=e+u=e+1+jwherej∈J(R). Soa=e+j. Therefore,Ris J-clean.

Lemma 2 LetRbe a J-clean ring. Then every nilpotent element belongs to the Jacobson radical.

Proof Assume thatRis a J-clean ring and seta∈N(R). Then there exists an idempotentse∈Id(R) andj∈J(R) such thata=e+j. Sincean=0, 1-a=1-e-j∈U(R), so 1-e∈U(R),e=0. HenceN(R)∈J(R).

Lemma 3 LetRbe a J-clean ring. Thenex-xe∈J(R) for anye∈Id(R) and anyx∈R.

Proof As (ex(1-e))2=0, we haveex(1-e)∈J(R) by Lemma 2 that isex-exe∈J(R), similarly, we havexe-exe∈J(R), hence we getex-xe∈J(R).

A ring is called right(left) quasi-duo ring if every maximal right(left) ideal is a two sided ideal.

Theorem 7 Every J-clean ringRis a right (left) quasi-duo ring.

Proof For any elementmin maximal right idealM, we havem=e+jwheree∈Id(R) andj∈J(R) since it is J-clean. Ifm=e+j, thenrm=re+rj,re=er+wfor anyr∈Rby Lemma 3 wherew∈J(R), sorm=er+rj+w. We knoww∈J(R), thuswbelongs to maximal right idealM,rj∈J(R),rjbelongs to maximal right idealM. Also whenm=e+j,e=m-j, bothmandjbelong to maximal right ideal which impliesebelongs to maximal right idealM,erbelongs to maximal right idealM,rm=er+rj+wbelongs to maximal right idealM. As a result, every maximal right ideal is also left ideal, it is two sided ideal.

Corollary 3 LetRbe a J-clean ring. ThenTn(R) is a right (left) quasi-duo ring.

ProofRis right (left) quasi-duo ring if and only ifTn(R) is right (left) quasi-duo ring by [5, Proposition 2.1], so we get the result by Theorem 7.

A ringRis called semiprimitive if its Jacobson radical is zero. An elementaof a ringRis nil-clean ifa=e+nwheree2=e∈Randnis a nilpotent. A ring is said to be nil clean ring if each of its elements is nil clean.

Corollary 4 LetRbe a semiprimitive ring. Then the following are equivalent:

1)Ris J-clean.

2)Ris left (or right) quasi-duo andRis nil clean.

3)Ris Boolean.

Proof 1)⟹2). Every J-clean ringRis right (left) quasi-duo ring by Theorem 7. As it is semiprimitive and it is Boolean, and so it is nil clean.

2)⟹3). AsRis nil clean, for left or right quasi-duo ring all nilpotent elements are inJ(R) by [5, Lemma 2.3], thusJ(R)=0 impliesN(R)=0, so it is Boolean.

3)⟹1). It is obvious.

LetDbe a ring,Cbe a subring ofDand 1D∈C, write:

S=R[D,C]={(d1,…,dn,c,c,…)|di∈D,c∈C,n≥1},

S′=R{D,C}={(d1,…,dn,cn+1,cn+2,…)|di∈D,cj∈C,n≥1}.

Here, the addition and multiplication are defined componentwise, bothS=R[D,C] andS=R{D,C} are rings with identities.

Lemma 4 1)J(S)=R[J(D),J(D)∩J(C)]. 2)J(S′)=R{J(D),J(D)∩J(C)}.

Proof See [6, Proposition 2.1.14].

Theorem 8 LetS=R[D,C]. Then the following conditions are equivalent:

1)S=R[D,C] is J-clean.

2)Dis J-clean and for anyc∈C, there exists an idempotente∈Csuch thatc-e∈J(D)∩J(C).

3)S′=R{D,C} is J-clean.

3)⟺2). It is similar to 1)⟺2).

Corollary 5 IfS=R[D,C] is J-clean, thenDandCare also J-clean.

3 Morita Contexts

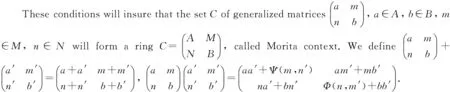
The next result can be found in [7].

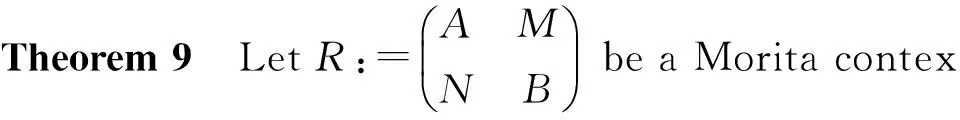
Proof IfRis J-clean ring, thenR/J(R) is Boolean andRis clean by Theorem 1. SoA/J(A) andB/J(B) are Boolean by Lemma 6,AandBare clean by [9,Theorem 3.3]. HenceA,Bare J-clean rings by Theorem 1. SinceR/J(R) is Boolean, one infersMN⊆J(A) andNM⊆J(B) by Lemma 6.

Conversely, supposeA,Bare J-clean, thenA/J(A),B/J(B) are Booleam andA,Bare clean rings. SoRis clean ring by [9,Theorem 3.3]. AndMN⊆J(A) andNM⊆J(B), by Lemma 6, we can knowR/J(R) is boolean. Therefore,Ris J-clean ring by Theorem 1.

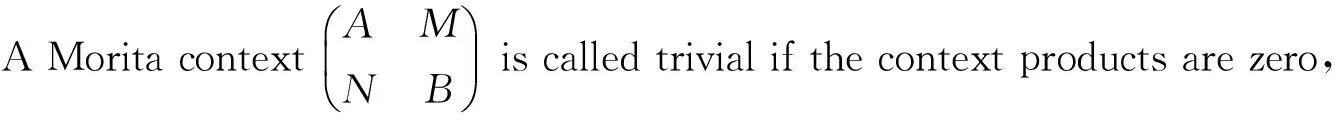
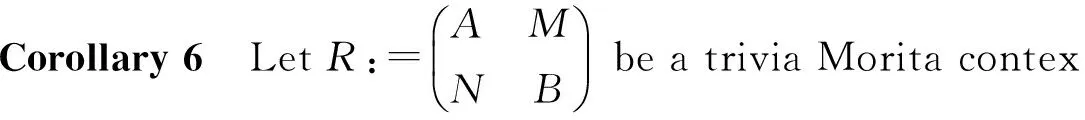
Lemma 7[10]A ringSis a generalized matrix ring overRif and only ifS=Ks(R) for somes∈C(R).

Corollary 7 LetRbe a ring withs∈C(R). ThenS=Ks(R) is J-clean if and only ifRis J-clean ands∈J(R).

Proof By Lemma 7, hereMN=NM=sR. SoMN⊆J(A)⟺s∈J(R) andNM⊆J(B)⟺s∈J(R). Therefore it is obvious by Theorem 9.

Corollary 7 clearly implies thatS=Ks2(R) is J-clean ifRis J-clean ands∈J(R). As explained below,S=Ks2=M2(R;s), a formal matrix ring defined bys.

Theorem 10 LetRbe a ring withs∈C(R). ThenMn(R;s) is J-clean if and only ifRis J-clean ands∈J(R).

(1)

and

yx=s2yn1x1n+s2yn2x2n+…+s2yn,n-1xn-1,n∈R.

(2)

IfMn(R;s) is J-clean, then, by Theorem 9,Ris J-clean andNM∈J(R). Thus, by (2),s2R=NM⊆J(R). AsR/J(R) is boolean, sos∈J(R).

Conversely, suppose thatRis J-clean ands∈J(R). By (1),MN⊆sA⊆J(R) andNM=s2R⊆J(R). Hence,Mn(R;s) is J-clean by Theorem 9.

Corollary 8 LetRbe a ring. Then the following are equivalent:

1)Ris J-clean.

3)Mn(R[[x]];x) is J-clean.

3)Mn(R[[x]]/(xm);x) is J-clean.

Proof 1)⟹2). Setf(x)=a0+a1x+a2x2+…, and 1-xf(x)=1-(a0x+a1x2+a2x3+…), sox∈J(R[[x]]). IfRis J-clean, thenR[[x]] is J-clean by Theorem 2. We can easily knowx∈C(R[[x]]), henceMn(R[[x]];x) is J-clean by Theorem 10.

2)⟹3). It is obvious.

3)⟹1). SupposeMn(R[[x]]/(xm);x) is J-clean, thenR[[x]]/(xm) is J-clean, soRis J-clean by Theorem 2.

[1] NICHOLSON W K. Lifting idempotents and exchange rings[J]. Trans Amer Math Soc,1977,229(5):269-278.

[2] DIESL A J. Classes of strongly clean rings[D]. Berkeley: University of California,2006.

[3] DIESL A J. Nil clean rings[J]. J Algebra,2013,383(6):197-211.

[4] CHEN H Y. On strongly J-clean rings[J]. Comm Algebra,2010,38(10):3790-3804.

[5] YU H P. On quasi-duo rings[J]. Glasgow Math J,1995,37(1):21-31.

[6] CHENG G P. The structure of ringR[D,C] and its characterizations[D]. Nanjing:Nanjing University,2006.

[7] SANDS A D. Radicals and Morita contexts[J]. J Algebra,1973,24(2):335-345.

[8] KOSAN T, WANG Z, ZHOU Y Q. Nil-clean and strongly nil-clean rings[J]. Pure Appl Algebra,2016,220(2):633-646.

[9] TANG G H, LI C N, ZHOU Y Q. Study of Morita contexts[J]. Comm Algebra,2014,42(4):1668-1681.

[10] KRYLOV P A. Isomorphism of generalized matrix rings[J]. Algebra Logic,2008,47(4):258-262.

[11] TANG G H, ZHOU Y Q. A class of formal matrix rings[J]. Linear Alg Appl,2013,438(12):4672-4688.

关于 J-clean环

胡小美, 陈焕艮

(杭州师范大学理学院, 浙江 杭州 310036)

10.3969/j.issn.1674-232X.2017.03.012

O153.3 MSC2010: 16D90;16N80;16S70 Article character: A

1674-232X(2017)03-0290-07