对偶统一模与有补统一模

徐芹芹，张慧

统一模的概念是Yager在［1］中推广和统一三角模和三角余模时提出来的，Weber S在［2］中提出了强否定算子的概念，［3］在研究三角模（三角余模）以及强否定算子的基础上对对偶三角模（三角余模）与有补三角模（三角余模）有一些研究.本文在统一模的基础上给出了对偶统一模与有补统一模的定义，并介绍了一种由已知的对偶（有补）统一模生成新的对偶（有补）统一模的方法.

1 预备知识

定义1.1 统一模U是指一个映射U：［0，1］2→ ［0，1］，它满足下列性质：

（1）交换性：U（a，b）＝U（b，a）；

（2）单调性：若a≥c，b≥d，则

U（a，b）≥U（c，d）

（3）结合性：U（U（a，b），c）＝U（a，U（b，c））；

（4）存在单位元：e∈ ［0，1］，对任意a∈ ［0，1］，U（e，a）＝a.

定义1.2 否定算子n是指映射：［0，1］→［0，1］，它单调减少且满足n（0）＝1和n（1）＝0，否定算子n称为强否定算子，如果n（n（x））＝x（∀x∈ ［0，1］）.

2 对偶统一模与有补统一模的定义

引理 若U是［0，1］上的统一模，单位元为e，令（a，b）＝n（U（n（a），n（b））），其中n为［0，1］上的强否定算子，则也是［0，1］上的统一模，且的单位元为n（e）.

证明 （1）交换性：（a，b）＝n（U（n（a），n（b）））＝n（U（n（b），n（a）））＝U（b，a）

（2）单调性：若a≥c，b≥d，则n（a）≤n（c），n（b）≤n（d），即（a，b）＝n（U（n（a），n（b）））≥n（U（n（c），n（d）））＝（c，d）

（3）结合性：（（a，b），c）＝n（U（n（n（U（n（a），n（b）））），n（c））） ＝n（U（U（n（a），n（b）），n（c））） ＝n（U（n（a），U（n（b），n（c）））＝n（U（n（a），n（n（U（n（b），n（c）））））＝（a，（b，c））

（4）存在单位元：（a，n（e））＝n（U（n（a），n（n（e））））＝n（U（n（a），e））＝n（n（a））＝a.

定义2.1 设U，都是［0，1］上的统一模，n为［0，1］上的强否定算子，且 ∀a，b∈ ［0，1］，有（a，b）＝n（U（n（a），n（b）））（等价于U（a，b）＝n（（n（a），n（b）））），则称和U关于n是对偶的.

定义2.2 设U是［0，1］上的统一模，单位元为e，若存在强否定算子n，使得对∀a∈（0，1），有U（a，n（a））＝n（e），则称U为有补统一 模.

3 一种构造新的对偶（有补）统一模的方法

定理 设g：［0，1］→ ［0，1］是严格单调增的连续函数，且g（0）＝0，g（1）＝1，用G表示g的反函数.又设U1，U2是［0，1］上的统一模，其单位元分别为e1，e2.n为［0，1］上的强否定算子，若∀a，b∈ ［0，1］，令

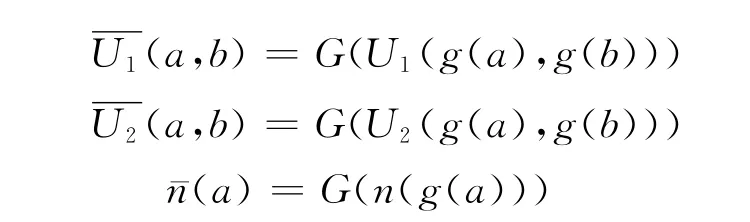
则也是［0，1］上的统一模，且其单位元分别为G（e1），G（e2）.为［0，1］上的强否定算子，且若U1，U2关于n是对偶的（有补的），则关于也是对偶的（有补的）.

同理可证也是统一模，且其单位元为G（e2）

其次证明是［0，1］上的强否定算子

最后证明关于是对偶的（有补的），∀a，b∈ ［0，1］，

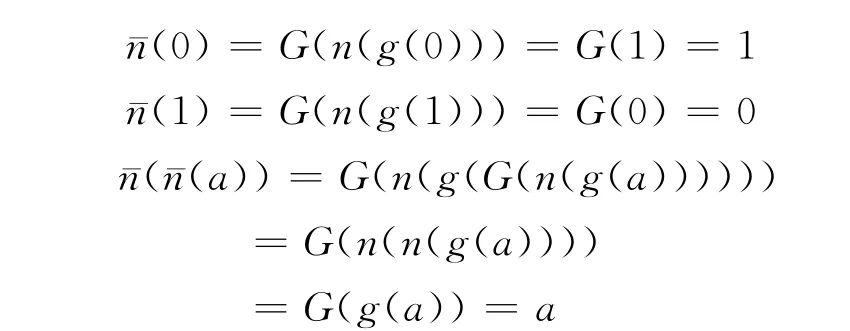
［1］Yager R R，Rybalov A.Uninorm aggregation operators，Fuzzy Sets and Systems，1996（80）：111－120.

［2］Weber S.A general concept of fuzzy connectives，negations and implications based on t-norms and t-conorms，Fuzzy Sets and Systems，1983（11）：15－134.

［3］胡宝清.模糊理论基础（第2版）［M］.武汉：武汉大学出版社，2004：22－26.