具有迁移效应和收获率的Hassell-Varley-Holling捕食者-食饵系统的周期解
刘子珍,刘秀湘
(华南师范大学数学科学学院,广州510631)
Hassell和 Varley[1]于1969年首次发现充裕的捕食者数量对捕食量有反作用的实验证据,并提出如下Hassell-Varley型的功能性反应(营养函数)

其中N和P分别是食饵和捕食者的种群数量,α是搜索效率,σ是衡量捕食者之间干扰的常数,被称为Hassell-Varley 常数.此后 Arditi和Akcakaya[2]、Schenk等[3]和 Sutherland[4]分别提出了下述 2 个营养函数

其中h>0表示捕食时间.这2个营养函数具有一般性.如果σ=0则分别为著名的Holling(II)和(III)功能性反应,故φ2和φ3分别被称为Hassell-Varley-Holling(II)和(III)功能性反应.如果σ=1,则φ2和φ3分别称为比率相关的功能性反应,相应的数学模型具有丰富的动力学行为并得到了广泛的研究[5-7].Cosner等[8]对 Hassell-Varley 常数给出一个分类:对具有相对固定数目个体而形成紧密团体的陆生捕食者可取σ=1/2;对具有相对固定数目个体而形成紧密团体的水生捕食者可取σ=1/3,对绝大部分捕食者而言,σ[1/2,1).这种类型的功能性反应很快引起了学者的注意[9-12].
种群的栖息地经常被看成几个斑块(patch)以进一步考虑到种群的迁徙[13].本文假设被捕食者在2个斑块之间进行迁徙而捕食者没有迁徙.设xi(t)(i=1,2)表示第i板块食饵种群在t时刻的密度,y(t)表示捕食者种群在第一个斑块t时刻的密度.由于2个斑块之间有食饵者迁移,我们把这个迁移效率记为 Di(t)(i=1,2).Ruan 等[14]指出了密度依赖的非线性死亡率对系统动力学有极为重要的影响.本文假设捕食者具有密度依赖的非线性死亡率,于是得到下述非自治的捕食者-食饵模型:

其中ai、d和β/α均为正值函数且分别代表食饵的内禀增长率、捕食者的死亡率和能量的转化率,ai/bi为食饵的环境容纳量,σ(0,1)表示捕食者的干扰.hi(t)(i=1,2,3)表示收获率.b3(t)为捕食者的密度相关的非线性死亡系数.利用基于度理论的连续定理证明了上述系统在适当条件下至少具有8个周期解.
首先给出常用的符号说明.记R+=[0,∞),.对R+上的有界函数f(t),定义

下面简要介绍度理论一些基本概念的相关引理.
设X,Z为实Banach空间.L:Dom L⊂X→Z为线性映射,N:X→X为连续映射.若dim Ker L=condim Im L<∞且Im L在Z中是闭的,则称L是指标为0的 Fredholm映射.若 L是指标为0的Fredholm映射且存在连续投射P:X→X及Q:Z→Z使得 Im P=Ker L,Ker Q=Im L=Im(I-Q),则L|DomL∩KerP:(I-P)X→Im L是可逆的并定义其逆映射 KP.设Ω是X的有界开集,若QN×[0,1])有界且KP(I-Q)N:×[0,1]→X 是紧的,则称映射N在×[0,1]是L-紧的.因为Im Q与 Ker L同构,故存在同构映射J:Im Q→Ker L.下面的引理见文献[15].
引理1 (连续定理)设L是指标为0的Fredholm映射且N在×[0,1]是 L-紧的.如果满足
(3)deg{JQN,Ω∩Ker L,0}≠0,则算子方程Lx=Nx在Dom上至少有一个解.
经过简单的计算有下面的引理.

有如下结论:
使用引理1来证明系统(1)正周期解的存在性.为此将系统(1)转化成相应的算子方程.作变换u1(t)=ln x1(t),u2(t)=ln x2(t),u3(t)=ln y(t),则系统(1)变为

易见若方程(2)有一ω-周期解 (u*1(t),u*2(t),是系统(1)的正ω-周期解.因此只需证明方程(2)有 ω-周期解即可.
令 X=Z={u=(u1,u2,u3)TC(R,R3):u(t+ω)=u(t)},‖u‖ =maxt[0,ω]|u1(t)|+maxt[0,ω]|u2(t)|+maxt[0,ω]|u3(t)|.于是 X,Z 均为Banach 空间.记ω



令 L:Dom L⊂X→Z,L u=(u'1,u'2,u'3)T,其中Dom L={u=(u1,u2,u3)TC(R,R3)},并令 N:X×[0,1]→Z 为利用这些记号可将方程(2)写成等价的算子方程L u=N u,uX.很明显 Ker L=R3,Im L={zZ:是Z的闭集,且dimKer L=codim Im L=3.故L是指标为0的Fredholm映射.定义2个投射P:X→X和Q:Z→Z分别为

易证P,Q是连续投射且Im P=Ker L,Ker Q=Im L=Im(I-Q),于是广义逆映射KP:Im L→Dom L∩Ker P存在且为


由Lebesgue控制收敛定理知QN和KP(I-Q)N是连续的.利用 Arzela-Ascoli定理,不难证明对任意有界开集Ω⊂X是紧的,而且QN)有界,所以对任意有界开集Ω⊂X,N在×[0,1]是 L-紧的.
为了方便定理证明过程表达,我们引进下列16个正数:

其中

本文的主要结果如下:
定理1 如果下列条件成立:

则系统(1)至少存在8个ω-正周期解.
证明 首先由引理2、条件(H1)和条件(H4)可得:

同时容易证明

根据引理1,只需寻找8个合适的有界开集Ωi(i=1,2,…,8)即可.相应于算子方程 Lx=λN(x,λ),λ(0,1)有

假设(u1(t),u2(t),u3(t))T是方程(3)对于某个(0,1)的一个 ω -周期解,则存在 ξi,ηiω](i=1,2,3),使得(t),i=1,2,3,且 u'i(ξi)=0,u'i(ηi)=0,i=1,2,3.根据方程(3)可得

分以下2种情形进行分析.
情形(i):u2(η2)≤u1(η1).此时由式(4)得

故得到 u2(η2)和 u1(η1)的上界

情形(ii):u2(η2)≥u1(η1).此时由式(5)有

也得 u2(η2)和 u1(η1)的上界

于是由式(10)、(11)可得

由式(6)知

于是得到

由式(4)、(13)有

因此
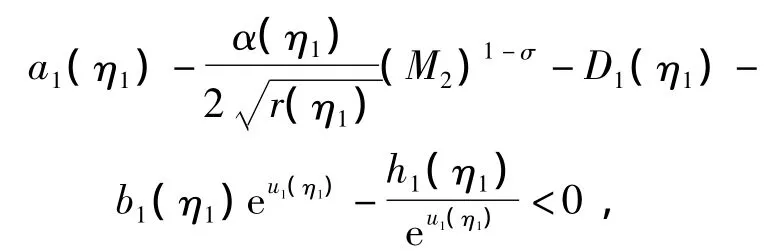
进一步有

即

类似地由式(7)有

考虑到式(4)可知

结合式(12)得

于是有

利用式(7)、(12)有

根据式(14)、(16)并结合条件(H1)和条件(H4)得到u1(η1)的估计:

再根据引理2得到u1(η1)的范围

由式(15)、(17)可知

则

利用式(5)得到

所以

即

根据式(8)不难看出

由式(5),有

从而

结合式(12)有

类似的,由式(8)、(12)不难得到

由式(20)、(22),结合(H2)和(H4)得到 u2(η2)的估计式

再根据引理2得到u2(η2)的所在区间为

由式(21)、(23)可得

从而

由式(6)可知

进一步则为

同理由式(9)可得

根据式(13)、(18)可得

利用式(6)有
即

进一步有

因此

另根据式(9)得到

由式(26)、(28)可得

即有u3(η3)的估计区间

同理由式(27)、(29)可得


从而知u3(ξ3)的估计区间

令

显然 Ωi(i=1,2,…,8)是 X 上的开集,Ωi∩Ωj= Ø(i,j=1,2,…,8,i≠j).从而 Ωi(i=1,2,…,8)满足引理1的条件(1).现往证引理1的条件(2)也成立,即要证若u∂Ωi∩Ker L= ∂Ωi∩R3时有 QN(u,0)≠0(i=1,2,…,8).用反证法,假设 QN(u,0)=0,则有:

即

易知代数方程组(32)有8个不同的解:


其中

由引理2,易验证:

由式(33)~(35)有

由于Ker L=Im Q,取 J=I.假设 u是式(32)在 Ωi(i=1,2,…,8)中的解,则

于是相应的Brouwer度为


从而证得Ωi(i=1,2,…,8)满足引理1的条件(3),至此证明了Ωi(i=1,2,…,8)满足引理1的所有条件,因此方程(2)至少有8个ω-周期解,即系统(1)至少有8个ω-正周期解.定理得证.
[1]Hassell M P,Varley G C.New inductive population model for insect parasites and its bearing on biological control[J].Nature,1969,223:1133-1137.
[2]Arditi R,Akcakaya H R.Underestimation of mutual interference of predators[J].Oeclogia,1990,83(3):358-361.
[3]Schenk D,Bersier L,Bacher S.An experimental test of the nature of predation:Neither prey-nor ratio-dependent[J].Journal of Animal Ecology,2005,74:86-91.
[4]Sutherland W J.Aggregation and the‘idea free distribution’[J].Journal of Animal Ecology,1983,52:821-828.
[5]Liu X,Huang L.Permanence and periodic solutions for a diffusive ratio-dependent predor-prey system[J].Applied Mathematical Modelling,2009,33:683-691.
[6]Pang P Y H,Wang M.Qualitative analysis of a ratio-dependent predator-prey with diffusion[J].Proceedings of the Royal Society of Edinburgh:Section A,2003,133:919-942.
[7]Xiao D,Ruan S.Global dynamics of a ratio-dependent predator-prey system[J].Journal of Mathematical Biology,2001,43:268-290.
[8]Cosner C,Deangelis D L,Ault JS,et al.Effect of spatial grouping on the functional response of predators[J].Theoretical Population Biology,1999,56:65-75.
[9]Hsu SB,Hwang TW,Kuang Y.Global dynamics of a predator-prey model with Hassell-Varley type functional response[J].Discrete and Continuous Dynamical systems:Series B,2008,10:857-871.
[10]刘秀湘,翁佩萱.具新功能性反应的捕食者—食饵系统的持续生存[J].生物数学学报,2007,22(5):799-804.Liu X,Weng PX.The permanence of predator-prey system with new functional response[J].Journal of Bioma thematics,2007,22(5):799-804.
[11]Liu X,Lou Y.Global dynamics for a predator-prey model[J].Journal of Mathematical Analysis and Applications,2010,371:323-340.
[12]钟敏玲,刘秀湘.具有Hassell-Varlay-Holling反应非自治捕食者-食饵系统的动力学分析[J].数学物理学报,2011,31A(5):1295-1310.Zhong M L,Liu X X.Dynamical analysis of a predator prey system with Hassell-Varlay-Holling functional response[J].Acta Mathematica Scientia,2011,31A(5):1295-1310.
[13]Fang H,Xiao Y.Existence ofmultiple periodic solutions for delay Lotka-Volterra competition patch systems with harvesting[J].Applied Mathematical Modelling,2009,33:1086-1096.
[14]Ruan SG,Ardito A,Ricciardi P,et al.Coexistence in competition models with density-dependent mortality[J].Comptes Rendus Biologies,2007,330(12):845-854.
[15]Gaines R E,Mawhin J L.Coindience degree and nonlinear differential equations[M]. Berlin:Springer,1977.
- 华南师范大学学报(自然科学版)的其它文章
- 我校《量子几何相位及其相关问题研究》项目获国家自然科学二等奖

