以全空间为-n-攀援集的系统
符和满, 谭 枫
(1.肇庆学院数学与统计学院,肇庆 526061; 2.华南师范大学数学科学学院,广州 510631)
设(X,f)是1个动力系统 (简称系统), 即X是一个含至少2个点的完备度量空间,f:X→X是1个连续映射. 设d表示度量空间X的度量.

令

2007年,Xiong等[2]对任意给定的Furstenberg族,定义了族-混沌, 使得原来备受关注的Li-Yorke混沌和分布混沌都成为某种特定族混沌, 即Li-Yorke混沌就是-混沌; 分布混沌就是混沌, 其中是所有正整数无限集构成的Furstenberg族,是所有上密度为1的正整数集构成的Furstenberg族. 在此基础上,Tan和Xiong[3]对给定的2个Furstenberg族和定义了(,)-混沌.
1997年,Mai[4]指出,存在(0,1)n(n≥2)上的自同胚以整个空间为Li-Yorke攀援集. Huang和Ye[5]证明了:存在“许多”非平凡的动力系统(X,f)以全空间X为Li-Yorke攀援集,其中X可以为可数个点构成的紧致度量空间、康托空间和任意维的连续统.Wang等[6]证明了不存在紧致的动力系统以全空间为分布攀援集, 并举出了只含可数多个点的非紧致的可逆系统,以全空间为分布攀援集.

1 预备知识
设F⊂+. 称F是一个thick集, 如果对任意的m+,存在amF,使得am,am+1,…,am+mF. 即F中包含了任意长的连续自然数片断. 全体thick集构成的集合是一个Furstenberg族,记为t.
最近, 熊金城等在文献[7]中引入如下一类新的Furstenberg族. 对每一个(0,1],定义
=F:
其中Fc=+-F. 并且定义.易见, 对每一个[0,1],均是Furstenberg族;且对任意的0≤1≤2≤1,有⊂.此外,⊂t.

对于U,V⊂X,记


称为集合U和V的碰撞时间集. 特别地, 当U是某独点集{x}时,简单地记Nf({x},V)为Nf(x,V), 称为点x在集合V中的回复时间集.


2 主要结果



定义1 设(X,f)为动力系统,[0,1],以及整数n≥2.设x1,x2,…,xnX两两互异,δ>0.记称是f的一个-δ-n-串, 如果以及对任意.


命题1 设(X,f)是一个动力系统, 实数δ>0,[0,1]以及整数n≥2. 则Xn-Δn(X)是一个-δ-n-串当且仅当在乘积系统(Xn,f(n))中,是Δn(X)的-趋附点, 又是Δn(X)的-δ-逃匿点.
定义2 设(X,f)为动力系统,C⊂X非空,[0,1]以及整数n≥2.
(i)给定δ>0. 称C是f的一个-δ-n-攀援集, 如果对于C中任意n个互异的点x1,x2,…,xn,(x1,x2,…,xn)都是f的一个-δ-n-串.
(ii)称C是f的一个-n-攀援集, 如果对于C中任意n个互异的点x1,x2,…,xn, 存在δ>0,使得(x1,x2,…,xn)是f的一个-δ-n-串.
注1 设(X,f)为动力系统, 整数n≥2.
定理1 设(X,f)是动力系统, 其中X紧致. 设族⊂t以及整数n≥2. 如果Δn(X)有-逃匿点,则f有distaln-串,即存在串(x1,…,xn)Xn-Δn(X)和δ>0,使得对任意的k≥0,有
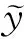


这是因为

由于每个(f(n))-l(Xn-[Δn(X)]δ)是紧致集, 从而

取


□
推论1 对任意的[0,1]和任意整数n≥2, 不存在紧致的动力系统,使得全空间就是-n-攀援集.
证明反证法. 倘若存在某紧致的动力系统(X,f),使得X就是-n-攀援集. 根据命题1可知,Δn(X)有-逃匿点. 注意到, 对任意的[0,1],⊂t. 故由定理1,f有一个distaln-串. 这与全空间是-n-攀援集矛盾.

令XS={xm:m≥0}, 其上的度量d取上所诱导的欧氏度量. 定义一个映射fS:XS→XS使得对每一个m≥0,fS(xm)=xm+1.则fS:XS→XS是连续映射.

则对于任意的整数n≥2,XS是一个-1-n-攀援集.
则对于任意的整数n≥2,XS是一个0-1-n-攀援集.


故对任意的ε>0,当k充分大时,若r2k-p 即对任意的ε>0, 另一方面, 由XS的定义, 可知当k充分大时,若r2k+1-p 即 综合上述,可得对于任意整数n≥2,XS是一个-1-n-攀援集. □ 例1 对任意的(0,1], 取序列S={sm}m+如下:s1=2,sm+1=m⎣其中r0=0,rm=s1+…+sm,m+且⎣a」代表不超过实数a的最大整数.则S满足定理3的(1).此时就该系统(XS,fS)来说,对于任意的整数n≥2,XS是一个-1-n-攀援集. 参考文献: [1] Schweieer B, Smítal J. Measure of chaos and a spectral decomposition of dynamical system on the interval[J]. Transactions of the American Mathematical Society, 1994, 334: 737-754. [2] Xiong J, Lv J, Tan F.Furstenberg family and chaos[J]. Science in China:Series A, 2007, 50(9): 1325-1333. [3] Tan F, Xiong J. Chaos via Furstenberg family couple[J]. Topology and Its Applications, 2009, 156(3): 525-532. [4] Mai J H. Continuous maps with the whole space being a scrambled set[J]. Chinese Science Bulletin, 1997, 42: 1494-1497. [5] Huang W, Ye X D. Homeoporphisms with the whole compacta being scrambled sets[J]. Ergodic Theory and Dynamical Systems, 2001, 21: 77-91. [6] Wang H, Liao G F, Fan Q J. A note on the map with the whole space being a scrambled set[J]. Nonlinear Analysis: Theory, Methods & Applications, 2009, 70(6): 2400-2402. [7] Xiong J C, Fu H M, Wang H Y. A class of Furstenberg families and their applications to chaotic dynamics[J]. Science China:Mathematics,2013,doi: 10.1007/s11425-013-4720-z.




