液压模块挂车刚柔耦合动态响应特性及摆臂疲劳分析

武俊达， 董大伟， 闫 兵， 王媛文， 孙玉华

(西南交通大学 机械工程学院,成都 610031)

液压模块挂车是一种特大、特重货物陆路运输工具，该车主要由4部分组成：结构、机构、液压系统与电气控制系统。其中车架属于大型空间结构，由多模块拼接而成，挂车被牵引行驶过程中受到来自路面不平度的振动激励时，车架弹性体的模态特征与刚柔耦合现象直接影响整体系统动态响应。液压系统与悬架结构结合成为液压悬挂系统，其用于支撑车架与货物载重、实现同油缸组的车轴载荷相等、调节车架高度以保持车架平面装载水平等功能。实际运行中，悬架摆臂已多次发生断裂故障，对挂车运行安全性与运输效率有很大的影响。

目前，关于悬架结构强度及疲劳方面的研究主要侧重于有限元静态分析方法[1-2]，忽略动态交变载荷的影响。为了实现车轴承受载荷相等，可采用平衡杆系模拟液压悬挂系统[3]，而所述的平衡杆系不能全面地反映液压系统的作用状态对悬架结构动载荷的影响。由于挂车具有多体系统动力学复杂的特点，已有学者把该车简化为一纵六轴线式，建立了多刚体系统动力学模型并进行液压悬挂系统动载荷分析[4]。因此，运用有限元分析与刚柔多体动力学仿真的相结合方法，应用于液压模块挂车动态响应及其摆臂疲劳强度研究具有工程意义与学术价值。

基于有限元分析法与多体动力学理论，运用ANSYS与ADAMS之间接口技术，建立15轴线式液压模块挂车刚柔耦合多体动力学模型，其中把车架看为柔性体，结合挂车振动试验验证模型的准确性。对挂车在不同路面等级与车速，考虑凹凸路面冲击下的运行工况，进行仿真计算并分析挂车动态响应特性。以多体动力学仿真计算结果为有限元分析的载荷，计算获得摆臂结构应力时间历程。选择合理的疲劳分析方法，进行摆臂疲劳寿命计算，包括：应力谱的循环计数、损伤累积及寿命预测。

1 基础理论

1.1 有限元模态分析的缩减自由度Guyan法

含n自由度结构有限元模型的动力平衡方程为:

(1)

式中，M、C与K为质量阻尼与刚度矩阵;u是节点位移矢量;f是随时间变化的载荷矢量。

缩减自由度Guyan法[5]的理论是将u分为主自由度um与从自由度us对应的位移向量，n=m+s。当没有载荷施加于从自由度上，且阻尼可忽略时，得到：

(2)

考虑静态情况时，式(2)可写为：

(3)

由式(3)，可得到：

{us}=-[Kss]-1[Ksm]{um}

(4)

[[Kmm]-[Kms][Kss]-1[Ksm]]{um}={fm}

(5)

(6)

式中，T为静态转换矩阵；I为m×m阶单位矩阵。缩减到主自由度上的刚度矩阵为：

(7)

用相同方法，将转换矩阵T扩展到式(2)中，得到缩减到主自由度上的质量矩矩阵与载荷矢量：

(8)

方程(2)可变为：

(9)

其自由度数缩减为主自由度数，比式(2)减少s个自由度。

1.2 柔性体动力学的模态综合Craig-Bampton法

ADAMS中采用模态综合技术Craig-Bampton法[6]求解柔性体运动方程。该方法将自由度系统分成边界自由度与内部自由度，对应两种模态：约束模态和固定边界正常模态。柔性体变形矢量U可用两种模态的物理位移及其对应模态坐标来表示，如公式(2)表示：

(10)

式中，UB、UI为边界与内部自由度的变形矢量；0为零矩阵；ΦIC,ΦIN为约束模态与正常模态中内部自由度的物理位移；qC、qN为约束模态和正常模态的模态坐标矢量；Φ成为模态转换矩阵。

总体刚度和质量矩阵转换可通过模态转换矩阵获得的：

(11)

(12)

动力平衡方程由模态坐标矢量通过模态转换矩阵表示如下：

(13)

(14)

在此基础上，求解柔性体模型在广义坐标的位移、速度与加速度向量和通过Lagrange方程式建立动力学微分方程[7]。考虑系统冲击时可采用传递矩阵法的刚柔耦合多体系统的冲击响应分析方法[8]，将冲量模型和碰撞接触模型与多体系统传递矩阵法结合，对系统进行动态响应分析。

1.3 液压系统的油液运动状态方程描述

目前，工程流体分析最广泛应用Lagrange方法描述流体的运动状态，其根据质量守恒定律、能量转化与守恒定律等及其油液的物理属性，建立油液力学微分方程组[9]。在此基础上，ADAMS/Hydraulic模块中采用Merrit方法的Navier-Stockes油液运动方程、液体连续方程、能量累积方程等来描述油液的运动状态方程(Equation of state for liquid)[10]

ADAMS中，基于Lagrange方程式，含液压系统的多体系统广义坐标由两个部分组成：第一部分是决定物体位形(位置和方向)和油缸的伸缩量；第二部分是决定油液状态的油液压力。系统的广义力除了外力和惯性力，还存在在油液体积变迁时对外做功。因此含多油缸联通的多体系统动力学微分方程包括：多体系统动力学方程[7]和油液的动力学方程。

2 液压模块挂车刚柔多体动力学模型的建立

2.1 车架有限元模型的建立

运用ANSYS建立车架有限元模型时，考虑鞍座支架对车架动态特性的影响，把鞍座支架看为车架的一部分。采用板壳单元Shell63与实体单元Solid45划分网格，结合刚性多节点约束方法来处理二者间的连接处。多体动力学模型中，柔性车架与其他刚体连接通过外部节点，该节点采用多点约束与集中质量单元模拟。材料属性设为普通合金结构钢16Mn。

由上述的缩减自由度Guyan法，对车架有限元模型进行模态求解并生成ADAMS所需要的模态中性文件。该方法的准确度将取决于车架有限元模型主自由度的合理选取，根据结构特点与外部节点数量，选取288阶车架主自由度模态、20阶固有频率模态。

2.2 柔性车架的处理

多体动力学模型的计算精度将取决于选取柔性体模态阶数。根据车架振动试验分析结果，车架模态频率主要集中在范围50Hz以内。因此，除了前6阶为刚体模态，对柔性车架选取20阶模态。与全自由度模态Block-Lanczos法的计算结果对比如表1所示，可看出：选取ANSYS中有限元模型的主自由度与ADAMS中柔性体的模态阶数能够反映车架动态特征，满足模型的计算精度。

模型采用鞍座支架的装载方式，为了实现柔性车架的鞍座支架与刚体货物间的连接，将大刚度的弹簧力元放置在二者间[11]。

2.3 液压回路系统的建立

液压悬挂包括悬臂Xi-j、摆臂Si-j、油缸Ci-j等主要部件，如图1所示，i=1, 2,…, 15为挂车的轴线，j=1, 2, 3表示每轴线横向有3个液压悬挂组。

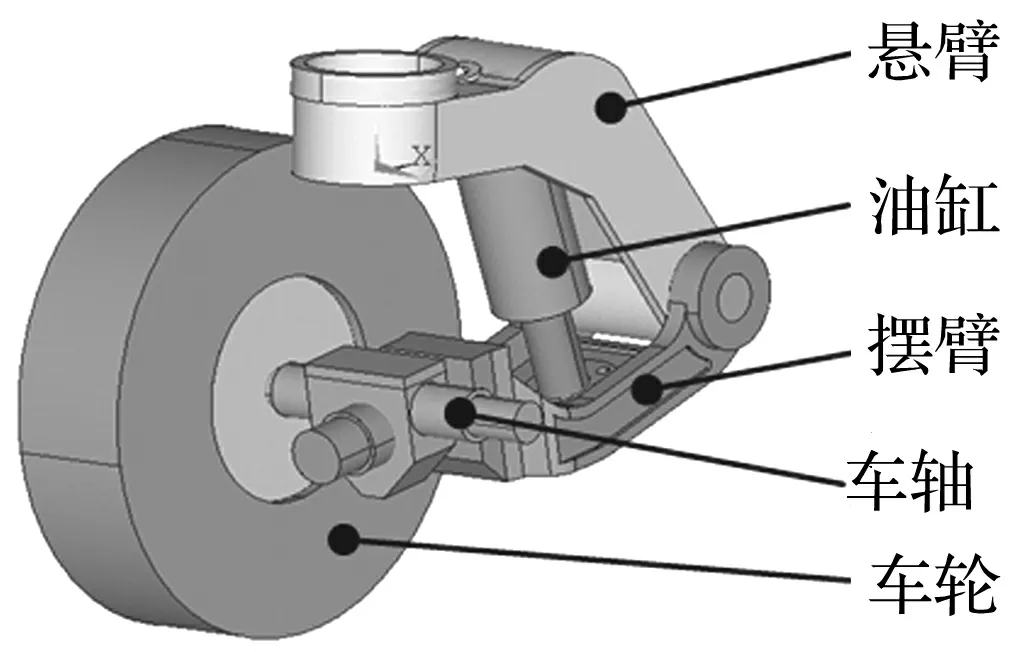
图1 液压悬挂组的主要部件

采用ADAMS/Hydraulic模块建立多油缸联通的液压回路系统时，假设；油缸体、活塞杆与油管是刚性体；忽略液压回路系统中的安全阀、溢流阀、换向阀等液压元件和热能效应。油缸间连接通过油管，油缸与油管的工作内涵特性取决于选取油管类型和几何参数。设计三点支撑方式的液压回路系统如下：前6个轴线的18个油缸互相连通成为一组，后9个轴线的27个油缸纵横交错连通而分成左右两组。选取油缸类型为Cylinder1f，其内径D=0.16 m；油管类型为Pipe_level1，其内径d=0.007 m；油液的体积弹性模量Eh=1 800 MPa、密度ρ=900 kg/m3[10]。

表1 缩减法与完全自由度法的固有频率对比

2.4 轮胎等效刚度计算

采用线性等效刚度KT的弹簧力元模拟轮胎，由车轮承受载荷Fw与轮胎变形量δ确定。用Komandi[12]提出经验公式计算轮胎变形量，每组轮轴有四个8.25R15型轮胎，计算得到KT=6.5×102kN/m，选取轮胎阻尼系数CT=1.5 kN·s/m。

2.5 路面不平度的时域激励加载

多体动力学模型采用激振台加载形式，以路面不平度为激励信号。大量试验测试结果表明：路面不平度的数据特性是平稳的，是具有零均值与各态历经的Gauss随机过程，可用功率谱密度来描述路面的统计特性。基于GB7031-1986《车辆振动输入——路面平度表示》标准[13]以及路面不平度的Fourier逆变换数值模拟方法[14,15]，考虑车速的影响，选取路面等级为B级、C级与D级；车速分别为2.22m/s、3.33 m/s、4.44 m/s与5.55 m/s；时间频率范围为0.5Hz≤f≤30 Hz；时间间隔为0.01 s，采样数据点数为212，仿真时长为40.96 s。运用MATLAP编制程序，计算获得路面不平度数据，ADAMS中用样条插值函数AKIPSPL编辑数据成为激振台的位移加载曲线。

图2 正弦形凹凸路面的几何

表2 正弦形凹凸路面的参数

为了描述凹凸不平度的复杂道路，采用正弦形曲线来实现。正弦形几何参数由正弦形幅值h、轴距L=1.6 m和正弦线凸起部分与前后车轮外公切线来确定，如图2所示。在此基础上，设计正弦形几何参数如表2所示。多体动力学模型中，纵向中间车轮(j=2)由C级路面不平度曲线分别加上正弦形长度2T的S1与S2为激励信号；纵向左右两行车轮(j=1, 3)由C级路面不平度为激励信号。

液压模块挂车刚柔多体动力学模型如图3所示：

图3 挂车刚柔多体动力学模型

3 挂车道路振动试验与仿真计算结果的对比

通过对挂车进行道路振动试验，获得车架与摆臂的动态垂向加速度频谱曲线，结合仿真计算结果来验证刚柔耦合多体系统动力学模型的准确性。

3.1 挂车振动试验分析

试验挂车装货物载重为282吨如图4所示，采用六个传感器单向加速度测量式：测点1到测点5位置分别在车架平面装载如图5所示；测点6位置在摆臂S5-2的轴头处。挂在水泥混凝土路面上运行，稳定车速为2.22 m/s。提取振动测试信号及其变换得到测试点的频谱曲线，如图6所示。

图4 15轴线式液压模块挂车

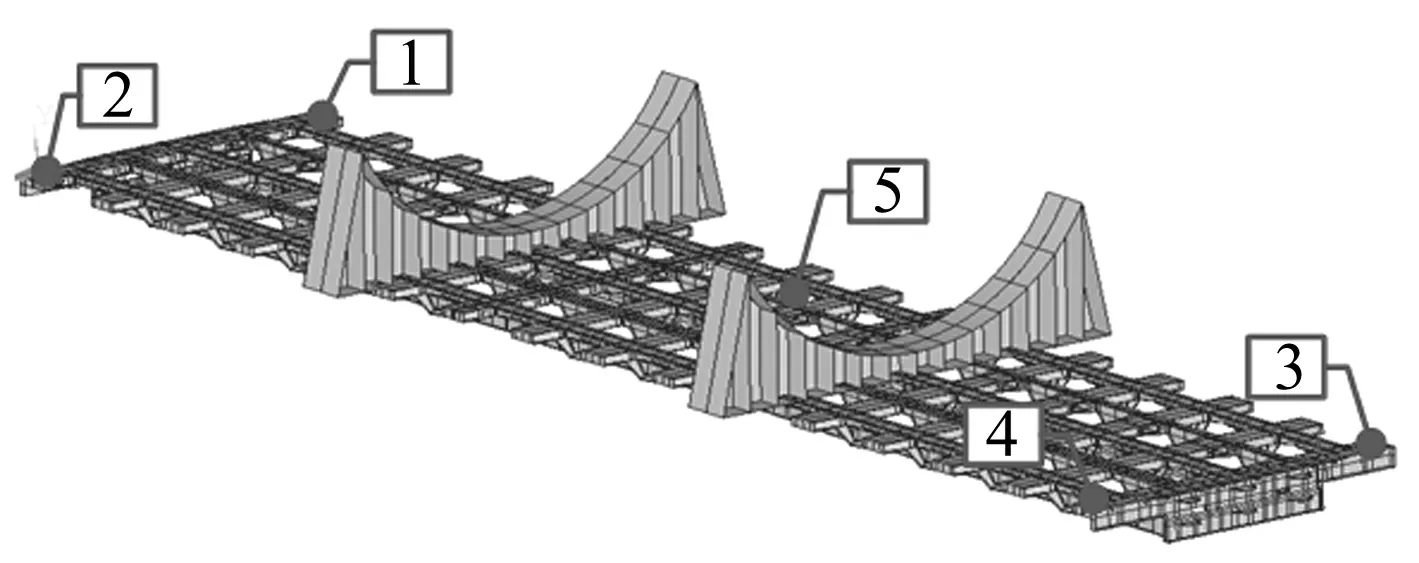
图5 车架各测点位置

3.2 振动试验与仿真计算结果的对比分析

挂车在B级路面、车速为2.22 m/s下的运行，仿真计算得到相应于各测点垂向加速度频谱曲线如图7所示。

从图6可看出，各测点都存在2.4 Hz的共振频率，表明该频率是实际整车振动频率，相应仿真计算结果出现在2.6 Hz的共振频率(加速度振幅为0.02 m/s2左右，如图7所示)。在ADAMS中运用线性模态分析功能对整车模型进行分析计算，得出在2.6 Hz是整车垂向平动模态振型。

各测点除了在2.4 Hz的共振频率，还存在比较明显的共振峰频率如测点1、2、3与4分别在9.9 Hz、10.45 Hz、10.45 Hz与9.6 Hz；测点5在17.4 Hz；悬架摆臂的测点6在25.2Hz。这些共振峰是挂车各组成部分的固有频率，与仿真计算结果对比偏差较小。

分析结果表明：仿真计算得到相应于振动试验测试点的频率谱变化规律相同，模态频率值基本一致，所建立的模型具有一定的准确性。

图6 试验测点的加速度频谱

图7 仿真计算的加速度频谱

4 挂车多体动力学仿真及其动态响应分析

4.1 挂车在不同路面等级与车速下的运行

挂车满载为500 t，装载方式通过三个鞍座支架，在不同路面等级与车速下的运行工况进行仿真计算，结果表明：摆臂S8-2质心垂向加速度均方根(RMS)值与地面承受车轮W8-2最大动载荷值随路面不平度与车速增加而增大，如图8与图9所示。

车轮Wi-j动载荷RMS值如图10所示，可看出：同属于一个油缸组的动载荷RMS值相对偏差较小。

柔性车架与悬臂Xi-j连接点的垂向加速度RMS值如图11所示。由于车架其他部位不受鞍座支架刚度的影响，其垂弯刚度小于车架与鞍座支架接触处。车轮受来自路面不平度激励时，振动能量转换为油液流动动能，其瞬时转化为油缸内的油液弹性势能。油缸通过对外做功，将其弹性势能转换为车架结构的弹性势能并使车架变形，车架与悬臂连接处的刚度较小部位会产生垂向变形量较大。因此，车架两边与前后车头部位的加速度向量大于纵向对称面与接近支架部分(第3、4、8、12与第13轴线)。

图8 摆臂S8-2质心加速度RMS值

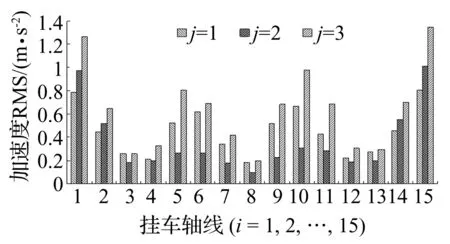
图11 车架与悬臂连接点的加速度RMS值

图12 摆臂质心加速度值

图13 车架与悬臂X8-2连接点的加速度

4.2 挂车在正弦形凹凸路面冲击下的运行

挂车在正弦形凹凸路面S2类、车速为2.22 m/s下的运行，摆臂S8-2质心垂向加速度如图12所示，轮胎与凹凸冲击时加速度值很明显剧烈增加。

由于液压悬挂系统能调整车架高度以保持车架水平，因此当任意车轮Wi-2受到正弦形凹凸路面冲击时，柔性车架的加速度也呈正弦形变化，如图13所示柔性车架与悬臂X8-2连接点的垂向加速度变化过程。

5 摆臂结构疲劳寿命预测

挂车运行中，摆臂已多次发生断裂故障，其断裂断面位置如图14所示。将作用于摆臂的动载荷，包括惯性载荷信息，转换成适用于有限元分析的数据格式，ANSYS中采用准静态叠加法[16]在离散的时间点上进行分析计算。根据摆臂结构的应力时间历程结果，选择合理的疲劳分析方法，对摆臂进行疲劳寿命预测。

图14 摆臂断裂故障的断面位置

5.1 摆臂结构有限元分析

选择对应车轮有相对较大动载荷的摆臂S8-2为疲劳分析的对象。采用实体单元Solid45进行摆臂划分网格，材料属性为铸铁QT450-10。提取作用于摆臂S8-2的载荷时间历程为1 000步数，进行有限元准静态叠加分析计算，获得摆臂有限元等效应力(Von-mises)分布如图15所示。

图15 摆臂有限元等效应力分布图

图16 摆臂最大等效应力值

图17 应力范围与平均值分布

摆臂应力集中部位出现在两边侧翼与底板的交接处，最大等效应力值σmax随路面不平度与车速增加而增大，其均大于材料屈服极限σS=331 MPa[17]，如图16所示。这表明危险部位应力水平已进入塑性状态。在D级路面、车速为5.55 km/h下的运行工况，，运用雨流计数法对危险点的应力时间历程进行应力统计分析，获得应力范围与平均值分布如图17所示。

5.2 疲劳寿命估算方法

根据有限元分析结果，危险点应力水平已进入塑性状态，其应力与应变不再是线性关系，塑性应变成为影响其疲劳寿命的主要因素。基于局部应力应变法，考虑平均应力的影响，采用Manson-Coffin-Baquin的Morrow平均应力修正公式[18]：

(15)

5.3 Miner线性累积损伤理

运用Miner线性累积损伤理论[19]，求解结构疲劳损伤及其疲劳寿命。首先求得在第i应力水平的应力幅范围Δσi与循环次数ni造成损伤Di，寿命为Ni，总累积损伤D等于1时结构发生疲劳破坏。Miner理论可用式(16)来描述

(16)

5.4 摆臂疲劳寿命预测

图18 摆臂疲劳寿命分布图

挂车在不同路面等级与车速下的运行，危险点的疲劳寿命如图19所示。若挂车使用系数为0.5，最小循环次数Nfmin=4.75×107，即寿命为30.1年，大于挂车使用年限为15年(包括，报废年限为10年和可延缓报废为5年)。这表明挂车在B级、C级与D级普通路面下的运行，摆臂不会出现疲劳断裂。

图19 挂车在普通路面下的运行，摆臂危险点的疲劳寿命

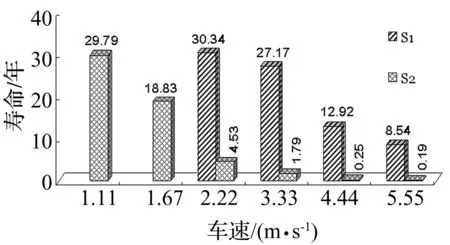
图20 挂车在凹凸路面下的运行工况，摆臂危险点的疲劳寿命

挂车在正弦形凹凸路面下的运行，摆臂危险点的疲劳寿命随正弦线幅值h与车速增加而明显减短，如图20所示。计算结果符合物流公司的运行记录：摆臂断裂故障常发生在凹凸不平的复杂路段。在凹凸路面S2类，若车速减小为1.67 m/s与1.11 m/s，危险点疲劳寿命可延长分别为18.83年与29.79年。

根据仿真计算结果，各运行工况可分为：适用的运行工况，即摆臂危险点的疲劳寿命大于挂车使用年限的；其余是不宜使用的运行工况，其疲劳寿命小于挂车使用年限。

6 结 论

(1) 基于有限元分析与刚柔多体动力学理论的相结合方法，建立了液压模块挂车刚柔耦合多体动力学模型。通过振动试验与仿真计算结果的对比分析表明：所建立的模型具有一定的准确性。挂车的部件垂向加速度与部件之间动载荷随路面不平度与车速增加而增大。模型中的液压回路系统能够有效地实现液压悬挂系统的基本功能。

(2) 根据结构有限元分析与疲劳寿命预测的计算结果得出：摆臂疲劳危险部位出现在已发生断裂的断面位置。挂车在B级～D级普通路面下的运行，危险点的疲劳寿命均大于挂车使用年限。而在正弦形凹凸路面冲击下，正弦形幅值与车速增加是引起摆臂危险点的疲劳寿命急剧减短。计算结果符合物流公司的运行记录：摆臂断裂故障常发生在凹凸不平的复杂路段。

(3) 根据仿真计算结果，可提出适用的运行工况以提高挂车的运行安全性与运输效率。研究方法与成果可为类似车辆的结构设计、优化及工程应用提供了参考依据。后续工作为对摆臂进行结构优化研究，改善危险部位的应力水平，并提高结构抗疲劳强度。

参 考 文 献

[1]张卫东, 莫旭辉, 彭劲松. 液压平板车悬架系统的有限元分析与结构优化[J]. 机械工程师, 2007, 10: 34-36.

ZHANG Wei-dong, MO Xu-hui, PENG Jin-song. Simulation and structural optimization about suspension of hydraulic conveyance vehicle[J]. Mechanical Engineer,2007,10:34-36.

[2]涂启养, 董大伟, 闫兵, 等. 某液压模块式组合挂车悬架结构件的强度及疲劳损伤分析[J]. 汽车科技, 2011, 3: 54-56.

TU Qi-yang, DONG Da-wei, YAN Bing, et al. Strength and fatigue analysis on the hydraulic modular assembled trailers suspension structure[J]. Auto Mobile Science & Technology, 2011, 03: 54-56.

[3]张宇探，马力，李冰. 液压模块组合挂车整体结构有限元计算分析[J]. 专用汽车, 2010, 1: 53-55.

ZHANG Yu-tan, MA Li, LI Bing. Calculation and analysis by FEM for whole structure of hydraulic module assembled trailer[J]. Special Purpose Vehicle, 2010, 1: 53-55.

[4]陈黝生. 组合挂车液压悬挂动载荷分析[D]. 上海: 同济大学工学, 2007.

[5]Guyan R J. Reduction of stiffness and mass matrices[J]. AIAA Journal, 1965, 3(2): 380.

[6]Craig R J, Bampton M. Coupling of substructures for dynamic analyses[J]. AIAA Journal, 1968, 6(7): 1313-1319.

[7]马星国, 尤小梅, 闻邦椿. 基于虚拟样机技术的曲轴多体动力学仿真[J]. 振动与冲击, 2008, 27(9): 155-157.

MA Xing-guo, YOU Xiao-mei, WEN Bang-chun. Multi-body dynamics simulation for a crankshaft system based on vitual prototype technology[J]. Journal of Vibration and Shock, 2008, 27(9): 155-157.

[8]隋立起, 郑钰琪, 王三民. 刚柔耦合多体系统的冲击响应分析方法及应用研究[J]. 振动与冲击, 2012, 31(15): 26-29.

SUI Li-qi, ZHENG Yu-qi, WANG San-min. Method of analysing impact response of multi-rigid-flexible system and its application[J]. Journal of Vibration and Shock, 2012, 31(15): 26-29.

[9]梁智权. 流体力学[M]. 重庆，重庆大学出版社, 2002.

[10]Herbert E. Merritt. Hydraulic Control Systems[M]. John Wiley & Sons Inc, 1967.

[11]谢基龙, 张燕, 谢云叶. 铁路凹底平车凹底架动态响应及其疲劳强度[J]. 机械工程学报, 2010, 46(16): 16-22.

XIE Ji-long, ZHANG Yan, XIE Yun-ye. Dynamic response and fatigue strength of dePublisheded center flat frame[J]. Journal of Mechanical Engineering, 2010, 46(16): 16-22.

[12]庄继德. 计算汽车地面力学[M]. 北京: 机械工业出版社, 2001.

[13]GB/T 7031-1986 车辆振动输入与路面平度表示方法[S]. 北京: 中国标准出版社, 1987.

[14]段虎明, 石峰, 谢飞, 等. 路面不平度研究综述[J]. 振动与冲击, 2009, 28(9): 95-101.

DUAN Hu-ming, SHI Feng, XIE Fei, et al. A survey of road roughness study[J]. Journal of Vibration and Shock, 2009, 28(9): 95-101.

[15]刘献栋, 邓志党, 高峰. 公路路面不平度的数值模拟方法研究[J]. 北京航空航天大学学报, 2003, 29(9), 843-846.

LIU Xian-dong, DENG Zhi-dang, GAO Feng. Research on the method of simulating road roughness numerically[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(9): 843-846.

[16]Bishop N W M, Sherratt F. Finite element based fatigue calculations[M]. National Agency for Finite Element Methods and Standards NAFEMS Ltd Published, 2000.

[17]陆明炯. 实用机械工程材料手册[M]. 沈阳: 辽宁科学技术出版社, 2004.

[18]David D W. Limits on morrow mean stress correction of manson-coffin life prediction models[C]. Proceedings of ASME Turbo Expo 2011, Vancouver, Canada, 2011: 85-92.

[19]李春祥, 李薇薇. 斜拉索风致动力疲劳损伤的研究[J]. 振动与冲击, 2009, 28(11): 61-66.

LI Chun-xiang, LI Wei-wei. Analysis of wind-induced fatigue damage of inclined cables[J]. Journal of Vibration and Shock, 2009, 28(11): 61-66.

[20]Atzori B, Meneghetti G, Ricotta M. A compatible method to summarise the low-and high-cycle fatigue test results of ductile irons and structural steels[J]. Giornata IGF Forni di Sopra (UD), 2012, 153-166.

[21]聂宏, 乔新. 一种新的应变疲劳材质参数估算方法[J]. 南京航空学院学报, 1992, 24(2): 226-231.

NIE Hong, QIAO Xin. A new prediction method of material behavior parameters for strain fatigue[J]. Journal of Nanjing Aeronautical Institute, 1992, 24(2): 226-231.

[22]聂宏, 常龙. 基于局部应力应变法估算高周疲劳寿命[J]. 南京航空航天大学学报, 2000, 32(1): 75-79.

NIE Hong, CHANG Long. High-Cycle fatigue life prediction based on local stress-strain method[J]. Ournal of Nanjing University of Aeronautics &Astronautiics,2000,32(1):75-79.