考虑裂纹效应的弹性板振动分析模型

刘文光, 严 铖

(南昌航空大学 航空制造工程学院，南昌 330063)

在航空航天领域，板的应用十分广泛，例如飞机进气道壁板、机翼下壁板、尾翼根部、发动机罩蒙皮以及发动机叶片等在一定条件下均可简化为板模型来研究。因为振动载荷一直贯穿于飞行器的发射、飞行直至完成使命的全过程，尤其是激励频率与飞行器结构某共振频率重合或相交时，结构可能萌生疲劳裂纹并不断扩展，甚至完全断裂，严重影响飞行器的安全可靠性。据不完全统计，在航空发动机的各类故障中，约有20%的故障是由于叶片含裂纹导致的[1]。由于裂纹的演变，使得含裂纹弹性板的动力学响应出现明显的非线性，给飞行器结构动力学设计带来很大困难。为此，研究探讨含裂纹弹性板的动力学行为与裂纹扩展的耦合效应对保障飞行器的安全可靠性具有重要的意义。

近年来，不少研究人员提出了各种计算弹性板固有频率的方法，如Lynn等[2]、Stahl等[3]等把含裂纹板的频率计算转化成Fredholm方程特征值的求解，而Maruyama等[4]通过试验研究不同裂纹尺度时板的固有频率，Hirano等[5]利用傅里叶变换方法预测弹性板的固有频率，Yuan等[6]运用Rayleigh-Ritz方法计算弹性板的固有频率，等等。为了探讨含裂纹弹性板的动力学特性，Khadem等[7]基于结构裂纹局部柔度理论提出一种含裂纹板的振动分析方法，Israr等[8]研究了含裂纹板的建模方法，并探讨了不同边界条件和加载条件下的振动特性，Wu等[9]研究了受面内周期载荷激励下含裂纹板的振动不稳定及其非线性响应特性，Krawczuk等[10]分析了含裂纹板的波传播及损伤识别问题。

尽管国内外学界和工程界在飞行器结构动力学设计时考虑了裂纹效应的影响，然而现行的设计方法鲜有人考虑结构动力学与疲劳裂纹变化之间的耦合效应，这很可能成为导致飞行器事故屡屡发生的重要原因。为了对飞行器结构进行精确的动力学设计，其根本任务在于能否准确地预测含裂纹板的振动行为与裂纹扩展规律，而解决问题的关键是建立含裂纹弹性板的动力学分析模型。为此，本文基于增加外部载荷和增加结构柔度在引起结构弹性变形方面具有等效性，提出一种耦合裂纹项的弹性板动力学建模方法，并以此为基础探讨含裂纹弹性板的若干动力学特性。

1 弹性板的动力学方程

一直以来，很多力学家都对弹性板的振动方程进行了严格的推导，但是这些推导并未考虑裂纹损伤对板振动特性的影响，导致经典的板振动方程难以应用于含裂纹板的振动与疲劳分析。于是不少研究者分析平板振动及其裂纹扩展特性时，常把裂纹作为自由边界来求解[9]。然而，振动环境下的结构裂纹可能伴随着振动激励发生扩展，尤其是共振状态时裂纹扩展非常迅速。如此条件下，若依然采用以上求解方法就非常困难。针对该问题，笔者认为考虑裂纹影响的最优策略则是把裂纹对弹性板振动的作用耦合到运动方程中。

1.1 建模策略

弹性板在振动载荷的循环激励下，其内部可能萌生裂纹并逐步扩展，而由此引起的结构柔度增加使得板在外部载荷不变的情况下，其弹性变形也会逐渐变大；同理，如果在受力平衡的弹性板的两侧逐渐增大外部载荷，即使不考虑裂纹所引起的结构柔度变化，弹性板的几何变形也会相应地增大。基于弹性变形等效原则，推导弹性板振动分析模型时可近似采用一个虚拟外部载荷来代替裂纹效应对变形的作用。

在理论推导之前，假定板的材料完全弹性、均质、各向同性；板的厚度均匀，远小于其长度和宽度；板的应变分量足够小，满足胡克定律；板的横向正应力分量相对其它方向应力分量很小，在应力应变关系中忽略不计；忽略剪切变形，且截面满足平面假设；忽略转动惯量、剪切力的影响。

(1)

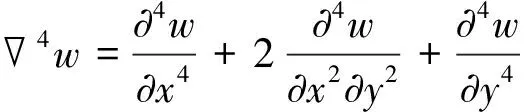
式中：w为横向位移，t为时间，ρ为材料密度，E为杨氏弹性模量，ν为泊松比，h为板厚，D为弯曲刚度，Pz为单位面积加载，nx、ny、nxy分别为单位长度的面力或薄膜力。

1.2 裂纹项表达式

(2)

(3)

式中：N∞、M∞分别是y=0处沿y方向单位长度的拉力和弯矩，αbb、αtt、αtb分别是无量纲弯曲柔度、拉伸柔度和拉弯耦合柔度，a为裂纹半宽。

将裂纹项代入运动方程，以Kirchhoff薄板内力条件[13]近似代替M∞，整理得：

(4)

2 弹性板动力学分析

对多数机械结构而言，线性振动模型已经足够满足需求，但结构内部存在裂纹或受到面内外部载荷时，继续使用线性模型可能不恰当。因为疲劳裂纹的引入，容易导致振动非线性，使结构振动响应变得无法预测。考虑到弹性板振动时，转动惯量和剪切变形对高阶模态的影响比对低阶模态的影响更为明显，所以下面分析只考虑第一阶模态对振动的贡献。假设板振动响应采用级数形式解[13]，通过Galerkin法可把含裂纹弹性板动力学系统简化成如下单自由度模型：

(5)

式中：Amn为任意幅值；Xm和Yn为弹性板的振型函数；ψmn是与时间有关的模态坐标；P0为作用在板上的集中力；坐标(x0,y0)为集中力的作用位置；δ表示Dirac函数。

利用Berger的研究，以板中面应变表达式第二项不变量引起的应变能推导出x和y方向单位长度上的面力nx和N∞的表达式[14]。把nx、N∞代入式(5)并通过Galerkin方法沿整个板面积分可得含平方和立方非线性项的动力学模型。进一步假设板受到外部力P0(t)=pcosΩmnt和线性阻尼作用，得到含平方和立方非线性项的振动模型：

(6)

式中：μ是阻尼系数，ωmn是弹性板固有频率，αmn和βmn是平方和立方非线性项系数，p是外部激励力幅值，Ωmn是外部激励力频率。

通过多尺度法[15]求解方程(6)得到含裂纹弹性板的频响特性，其特性方程如下:

(7)

式中：σmn是调谐参数，它是激励频率和共振频率接近程度的描述，α是响应幅值。

假设裂纹只沿x方向径直扩展，忽略其它方向动应力对裂纹疲劳扩展的影响，可得到裂纹顶端表面位置y方向动应力σy的近似计算式

(8)

3 算 例

考虑图1所示含裂纹铝板，通过上述理论分析可探讨裂纹效应对结构振动特性的影响。假定板的四边简支，尺寸为长l1、宽l2、厚h，l1、l2≫h，在弹性板中央有一宽为2a的裂纹，裂纹方向与x轴平行。分析时，用无损弹性板的振型函数近似代替含裂纹板的振型函数[16]

图1 含裂纹弹性板模型

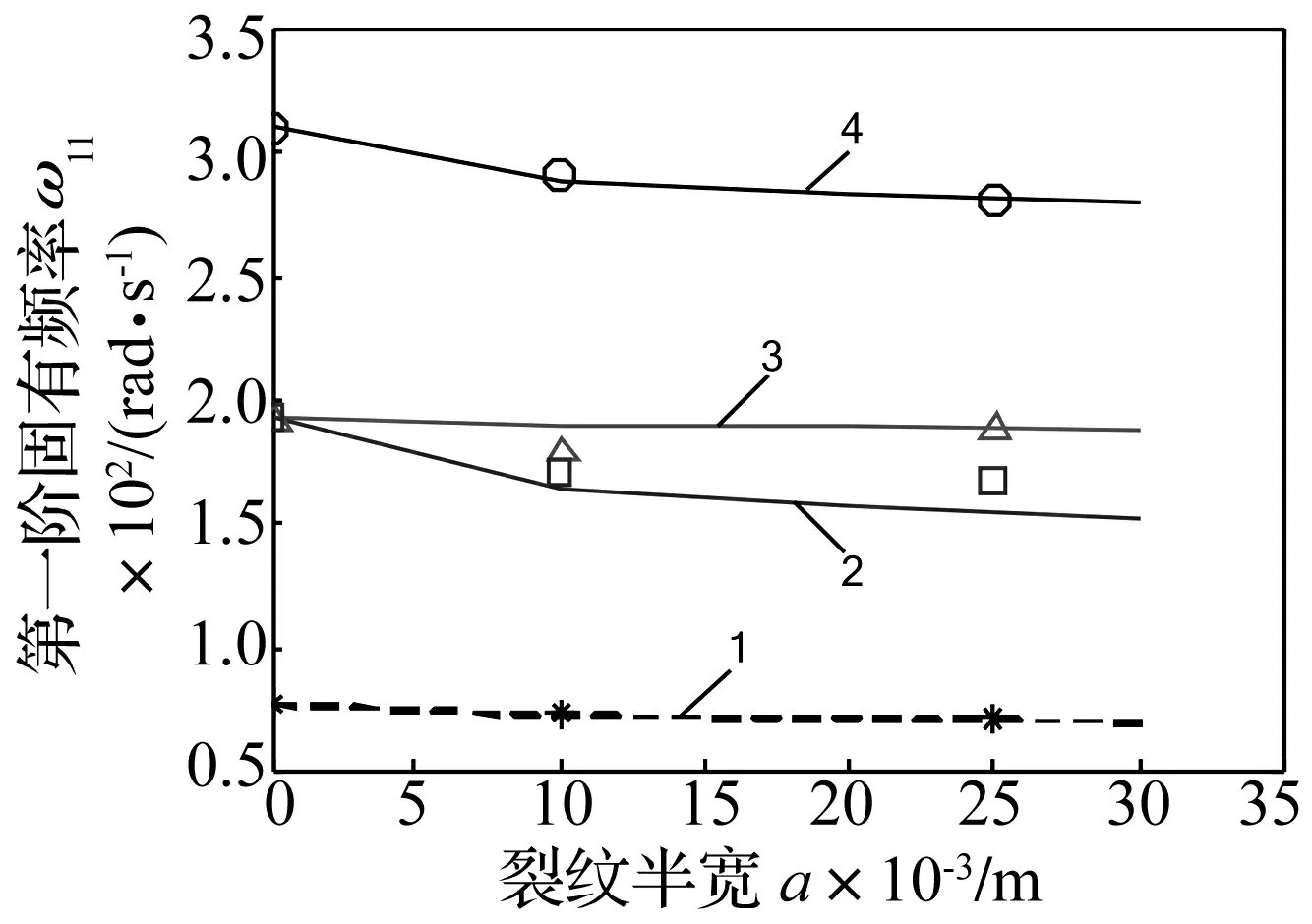
1.l1=1 m、l2=1, 2. l1=0.5、l2=1 m, 3. l1=1 m、l2=0.5 m, 4. l1=0.5 m、l2=0.5 m— 本文计算结果， ○、△、□、*文献[8]的结果

计算时，相对裂纹深度ξ取0.6，对应局部柔度系数αtt=3.553、αbb=1.079、αtb=1.932[17]。铝合金弹性模量E=70.3 GPa、密度ρ=2 660 kg/m3、泊松比v=0.33[11]。通过本文模型得到了裂纹板的第一阶固有频率，并与文献[8]比较，见图2。分析发现两者基本吻合，表明模型具有一定的可行性。

在板坐标(0.375, 0.375)处施加10牛顿的交变载荷，并考虑线性阻尼μ=γωmn的作用，γ是弹性板模态阻尼因子。计算表明，弹性板的振动呈明显的非线性，板尺寸和裂纹尺度对振动非线性有较强的影响，如图3、4所示。在同裂纹情况下，长宽相等时，随着板尺寸的增大振动非线性减弱；板长大于板宽时，非线性特征呈弹簧渐硬特性；反之非线性特征呈弹簧渐软特性。长宽比确定时，随着裂纹尺度的不断增大，振动非线性逐渐增强。当裂纹尺度非常小(如0.000 01 m)，裂纹所引起的非线性特征不是很明显，近似于线性问题。

裂纹顶端表面的动应力幅值是驱动裂纹疲劳扩展的主要因素，它受到激励力位置以及阻尼大小的控制，如图5、6所示。激励力位置距离边界位置越远，动应力幅值越大。随着板受到阻尼值的不断增大，裂纹顶端的动应力幅值急剧下降，阻尼对响应幅值具有明显的抑制。

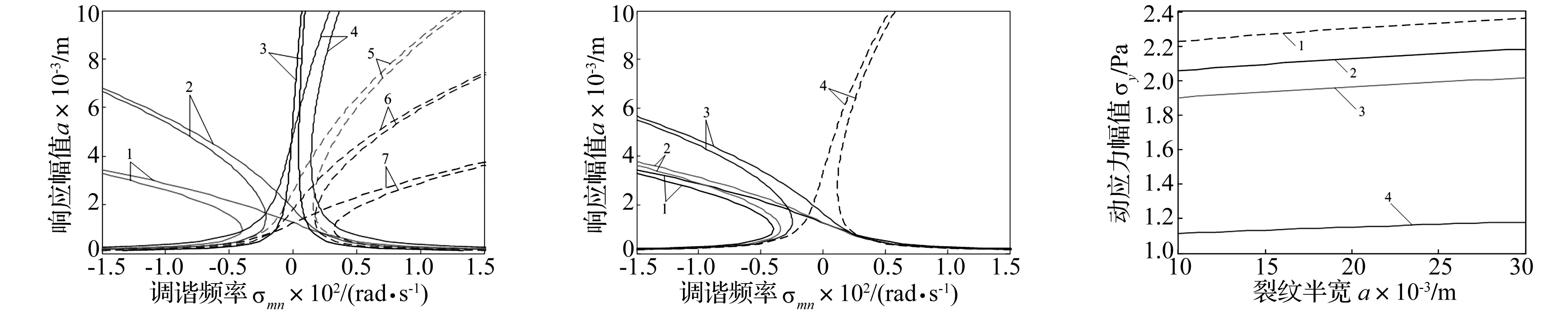
1.l1=1 m、l2=0.5 m, 2. l1=2 m、l2=1 m, 3. l1=2 m、l2=2 m, 4. l1=1 m、l2=1 m 5. l1=0.5 m、l2=0.5 m, 6. l1=1 m、l2=2 m, 7. l1=0.5 m、l2=1 m

1. γ=0.001, 2. γ=0.003, 3. γ=0.005, 4. γ=0.007

4 结 论

(1) 基于变形等效原则，以虚拟的外部载荷近似代替裂纹，通过力学平衡原理推导了含裂纹弹性板的动力学方程，在此基础上，结合Galerkin法和Berger经验把含裂纹弹性板振动系统简化成单自由度非线性振动模型。

(2) 以四边简支含裂纹板为对象，探讨了弹性板尺寸、裂纹尺度、阻尼以及激励力位置对振动非线性特性和动应力幅值的影响。

(3) 结论表明，耦合裂纹项的弹性板动力学模型考虑了振动行为与裂纹扩展的耦合效应，为板结构动力学设计提供了理论工具。

参 考 文 献

[1]陆榕海,廖振魁. 略论发动机涡轮叶片的振动疲劳[J].洪都科技,1997,(1):19-23.

LU Rong-hai, LIAO Zhen-kui. Briefing on vibration fatigue of turbine blade [J]. Hongdu Science and Technology, 1997, (1):19-23.

[2]Lynn P P, Kumbasar N. Free vibration of thin rectangular plates having narrow cracks with supported edge[C]//Proceeding of the 10thMidwestern Mechanics Conference, Colorado State University, Fort Collins, Colorado, in Developments in Mechanics, 1967:911-928.

[3]Stahl B, Keer L M. Vibration and stability of cracked rectangular plates [J]. International Journal of Solid and Structures, 1972, 8(1):69-91.

[4]Maruyama K, Ichinomiya O. Experimental study of free vibration of clamped rectangular plates with straight narrow slits [J]. Japan Society of Mechanical Engineers, 1989, 32(2):187-193.

[5]Hirano Y, Okazaki K. Vibration of cracked rectangular plates [J]. Bull of JSME, 1980, 23(179):732-740.

[6]Yuan J, Dickson S M. The flexural vibration of rectangular plate systems approached by using artificial spring in the Rayleigh-Ritz method [J]. Journal of Sound and Vibration, 1992, 159(1):39-55.

[7]Khadem S E, Rezaee M. Introduction of modified comparison functions for vibration analysis of a rectangular cracked plate [J]. Journal of Sound and Vibration, 2000, 236(2):245-258.

[8]Israr A, Cartmell M P, Manoach E, et al. Analytical modeling and vibration analysis of partially cracked rectangular plates with different boundary conditions and loading[J].Journal of Applied Mechanics, 2009,76(2): 11005-11013.

[9]Wu G Y, Shih Y S. Dynamic instability of rectangular plate with an edge crack [J]. Computers and Structures, 2005, 84(1):1-10.

[10]Krawczuk M, Palacz M, Ostachowicz W. Wave propagation in plate structures for crack detection [J]. Finite Elements in Analysis and Design, 2004, 40 (9):991-1004.

[11]刘文光,贺红林.含裂纹板的振动疲劳裂纹扩展耦合分析[J].中国机械工程,2012,23(19):2301-2305.

LIU Wen-guang, HE Hong-lin. Coupling analysis of vibration fatigue crack growth for a cracked plate[J]. China Mechanical Engineering, 2012, 23(19):2301-2305.

[12]Rice J R, Levy N. The part through surface crack in an elastic plate [J]. Journal of Applied Mechanics, 1972, 3(1):185-194.

[13]曹志远. 板壳振动理论[M]. 北京:中国铁道出版社, 1989.

[14]Berger H M. A new approach to the analysis of large deflection of plates [J]. Journal of Applied Mechanics, 1955, 22(3):465-472.

[15]胡海岩.应用非线性动力学[M].北京:航空工业出版社,2000.

[16]Berthelot J M. Dynamics of composite materials and structures [M]. Institute for Advanced Materials and Mechanics, Springer, New York, 1999.

[17]刘文光,陈国平.含裂纹悬臂梁的振动与疲劳耦合分析[J].振动与冲击, 2011,30(5): 140-144.

LIU Wen-guang, CHEN Guo-ping. Coupling analysis for vibration and fatigue of a cracked beam [J]. Journal of Vibration and Shock, 2011, 30(5): 140-144.