两自由度弯扭耦合涡轮机械叶片动力学分析

王 丹， 陈予恕， 曹庆杰， 熊冶平

(1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.南安普顿大学 工程与环境学院, 南安普顿 SO17 1BJ英国)

叶轮机械所处的工况十分复杂，叶片和流经的流体之间时刻进行能量的传输或转换，因此这类机械的结构特点和工作原理决定了其内部流动的复杂性。柔性叶片较之刚性叶片，更容易受到气动力的作用，产生结构变形，发生共振，因而存在着巨大的安全隐患。为了提高叶片与流体进行能量传输的效率，同时预防叶片发生颤振，对叶片的气动弹性问题进行研究是非常必要的。由于叶片本身结构的设计，实际工程应用中多采用数值模拟如边界元、有限元的方法研究其气动弹性问题。Jadic等[1]利用时间推进方法分别研究了流体-叶片在带有连续涡和不带有连续涡的一致均匀流作用下的耦合运动。其研究表明，颤振的发生不会导致灾难性的失效问题，而是叶片会发生极限环运动，并且其振幅很大程度上依赖于结构的非线性因素。So等[2]利用边界元方法研究了在两列平行涡激作用下，NACA0012翼型的流体激振响应问题。他们的研究结果表明，空气动力学和结构共振发生在相同的共振参数比c/d，而与截面的几何形状和作用到的叶片上的平均气动力载荷无关。Lau等[3]利用时间推进边界元方法详细的研究了两个参数s/c(静子的几何设计参数，静子叶片排叶片间距与叶片弦长之比)和c/d(归一化频率参数，与转子尾流的通过频率有关)对于叶片与漩涡耦合作用的影响。

在实际的工程应用中，对由于流固耦合作用引起的涡轮机械叶片的疲劳寿命预测是非常重要的。Sanders等[4]从理论上分析了转子叶片在转子-静子耦合作用下受到的气动力和气动力矩。在以前的研究中,转子尾流是作用到静子叶片上的一个主要的外激励源[5]。Hodson等[6-7]研究了转子尾迹扰流的主要特点。Cicatell等[8-9]研究了涡轮叶片的尾迹流对静子叶片的作用。Lau等[3]研究了一个由五个叶片组成的线性叶片排在尾流激振作用下的疲劳寿命预测。

本文的主要目的是在亚音速、低马赫数条件下,通过定性分析方法，对受准定常气动力作用的叶片发生临界颤振进行预测和控制。建立了一个二自由度具有立方非线性涡轮机械叶片的截面模型，根据Lagrange原理建立了叶片发生颤振时的运动方程；通过数值模拟研究来流速度对振幅的影响；利用平均法理论研究了叶片颤振时的非线性动力学行为；利用能量法分析了叶片在能量输入和输出情况下的稳定特性。

1 建模

1.1 二自由度叶片截面模型

图1 二自由度叶片顶端截面模型

1.2 弯扭耦合系统的运动方程

由图1利用拉格朗日定理，得到结构振动方程，

(1)

根据Grossman’s 的准定常气动力模型,得到二自由度系统受到的气动力和气动力矩如下:

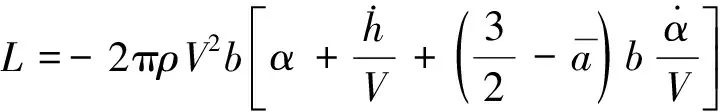
进一步,假设振动为小角度, cosα≈1,sinα≈α

对方程组(1)进行无量纲化,得到如下方程组:

(2a)

(2b)

无量纲参数变换为,

1.3 耦合系统的数值分析

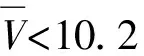
图2 无量纲来流速度对弯曲、扭转振幅的影响(a1为弯曲振动振幅，a2为扭转振动振幅)

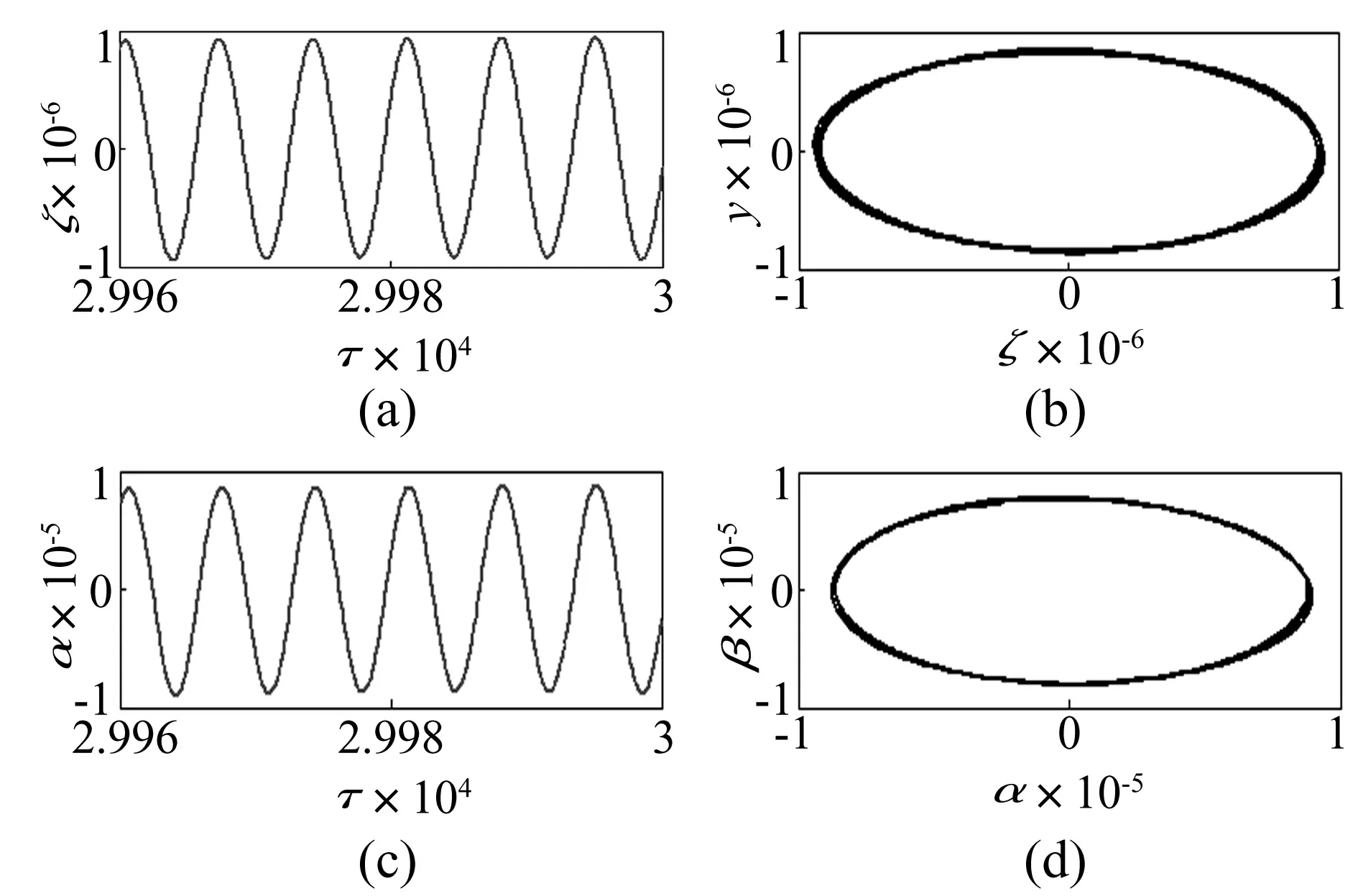
图3 当时的时间历程图和相图：弯曲振动 (a), (b)和扭转振动(c), (d)

图4 当时的时间历程图和相图：弯曲振动(a), (b)和扭转振动(c), (d)

图5 当时的时间历程图和相图：弯曲振动(a), (b)和扭转振动(c), (d)

2 动力学分析

2.1 平均法分析

工程技术中，平均法由于很好的保持了系统的一阶近似稳态解，因此常被用来研究强迫振动系统、自激振动系统等动态特性，尤其在非线性动力学领域被广泛应用。在气动力和气动力矩的作用下，叶片极易发生颤振，因为颤振是一种结构与气流相互耦合作用下的自激振动，所以其解具有稳态临界性质。根据平均法原理,设系统(2)在两个自由度上的稳态振动形式分别为，

ξ=Acos(ωτ+φ1)
α=Bcos(ωτ+φ2)

(3)

其中A,B,φ1,φ2是关于时间τ的慢变参数。根据平均法的思想，得到A,B,φ1,φ2关于时间τ的一阶导数分别为:

(4)

其中φ1=ωτ+φ1,φ2=ωτ+φ2以及

(5)

(6)

(7)

(8)

(9)

(10)

通过(9)式，得到振动频率的表达式为:

(11)

其中，

将得到频率表达式代到等式(10)中，得到振幅A,B与振动频率ω的关系，如图6、图7所示。

根据式(11)，得到振动频率与无量纲来流速度、频率比之间的关系如图8、图9所示。

图6 弯曲振动方向上的振幅A与振动频率ω关系图:参数为=0.75,xα=0.1,α=0.5, μ=640,Rξ=0.5,Rα=0.5,ζξ=0.016,ζα=0.021,=0.365,B=0.2,=11

图9 振动频率ω与频率比之间的关系图，绿线为ω1，红线为

将式(11)代到式(10)中，得到振幅A,B和系统参数的非线性关系图如图10～图15所示。

这些关系图定性的反映了该耦合系统的振动特性，通过上述图中给出的结果，可以对其振动进行预测与控制。

2.2 系统的能量传递分析

能量流方法近年来被广泛用于工程中复杂结构以及振动控制系统的振动分析，性能评估、振动控制以及动力学设计等[10-13]。其中，很多研究都是基于线性理论，而利用能量流方法对于非线性系统的研究有限。该部分根据能量流研究非线性系统的理论与方法[15]，通过研究系统在每个振动周期内的平均能量，可以对系统的稳定性进行预测，从而避免系统因吸收能量发生大幅颤振所对结构造成巨大的破坏。系统(1)在每个振动周期内的平均输入能量为:

图10 弯曲振动方向振幅A与非线性刚度系数Rξ的非线性关系,=0.75,xα=0.1,α=0.5, μ=640,Rα=0.2,=0.365,ζξ=0.016,ζα=0.021,=10.4,A=0.2,B=0.5

(12)

系统由于阻尼作用,在每个周期内消耗的平均能量为:

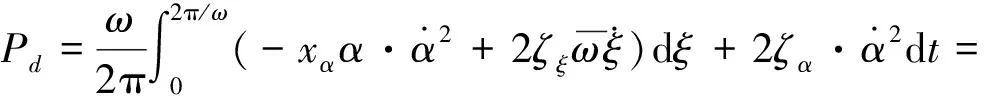
(13)

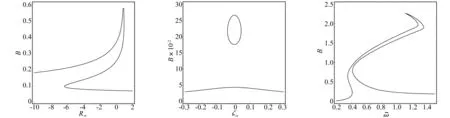
图13 弯曲振动方向振幅B与非线性刚度系数Rα的非线性关系, =0.75,xα=0.1,α=0.5, μ=640,Rξ=0.5,ζξ=0.016,ζα=0.021,=11,=0.365,A=0.2

图16 相位差取θ(π/2,π/4,0)不同值时系统每个周期内平均吸收能量Pin与无量纲来流速关系：系统参数分别为=0.75,μ=640,ω=0.5,A=0.5,B=0.5

系统每个周期内平均耗散的能量与振动频率ω之间的关系如图18所示。

从图18可以看出，当相位差θ分别取0,π/4,π/2时，系统消耗能量Pd都随着振动频率ω的增加而增大。

3 结 论

文章针对涡轮机械叶片所处的复杂的工作环境，建立了二自由度弯扭耦合并且具有立方非线性的叶片截面模型，并对其进行了动力学分析。在叶片颤振过程中，当来流速度超过临界值时，其振动幅值随着来流速度的增加而增大。利用平均法得到了系统振动的幅值及其频率之间的关系以及两个自由度上振幅与系统参数之间的关系。通过能量法分析了系统在一个周期内的稳定性情况，从而为预测实际系统中叶片发生颤振提供了理论依据。

参 考 文 献

[1]Jadic I, So R M C, Mignolet M P. Analysis of fluid-structure interactions using a time-marching technique[J].Journal of Fluids and Structures, 1998,12:631-654.

[2]So R M C, Jadic I, Mignolet M P. Fluid-structure resonance produced by oncoming alternating vortices[J]. Journal of Fluids and Structures, 1999,13:519-548.

[3]Lau Y L, Leung R C K, So R M C. Vortex-induced vibration effect on fatigue life estimate of turbine blades[J]. Journal of Sound and Vibration, 2007,307 :698-719.

[4]Sanders A J, Fleeter S. Vane row indexing for passive vibration control of axial-flow turbomachine rotors[J]. Journal of Propulsion and Power , 1999, 15: 650-657.

[5]Naudascher E, Rockwell D . Flow induced vibrations: an engineering guide[M]. A. A. Balkema, Rotterdam, 1994.3.

[6]Hodson H P, Dawes W N. On the interpretation of measured profile losses in unsteady wake-turbine blade interaction studies[J]. Journal of Turbomachinery, 1996, 120: 276-284.

[7]Hodson H P, Howell R J. Bladerow interactions, transition, and high-lift aerofoils in low-pressure turbines[J]. Annual Review of Fluid Mechanics, 2005,37:71-98.

[8]Cicatelli G, Sieverding C H. The effect of vortex shedding on the unsteady pressure distribution around the trailing edge of a turbine blade[J].Journal of Turbomachinery, 1997, 119 :810-819.

[9]Sieverding C H, Richard H, Desse J M. Turbine blade trailing edge flow characteristics at high subsonic outlet Mach number[J]. Journal of Turbomachinery, 2003,125: 298-309.

[10]Mandal N K, Biswas S. Vibration power flow: a critical review. [J].The shock and vib. Digest,2005,37:3-11.

[11]Xiong Y P, Xing J T , Price W G. Hybrid active and passive control of vibratory power flow in flexible isolation systems[J]. Shock and Vib. 2000,239:275-295.

[12]Xiong Y P, Xing J T P, Price W G. A gerneral linear mathematical model of power flow analysis and control for integrated structure-control systems[J]. Joneral of Sound and Vibration,2003,267:301-334.

[13]Xiong Y P, Xing J T, Price W G. Interactive power flow characteristics of an integratedd equipment-nonlinear isolator-travelling flexible ship excited by sea waves[J]. Journal of Sound and Vibration,2005, 287(1-2):245-276.

[14]Xiong Y P, Cao Q J. Power flow characteristics of coupled linear and nonlinear oscillators with irrational nonlinear stiffness[C]. ENOC,2011, Rome,Italy,24-29.