基于小波变换的时变及典型非线性振动系统识别

黄东梅, 周 实, 任伟新,3

(1.中南大学 土木工程学院，长沙 410075；2. 高速铁路建造技术国家工程实验室，长沙 410075;3.合肥工业大学 土木与水利工程学院，合肥 230009)

非线性振动现象在控制工程、机械工程、土木工程等领域广泛存在，非线性振动系统的识别是现代振动分析领域中研究的热点和难点问题。总的来说，非线性振动系统的识别方法可以分为基于信号处理技术的方法、时间序列分析类方法、子空间类方法等[1-9]。近年来，时频联合分析被广泛应用于线性系统模态参数识别方法中，同时也为弱非线性系统的辨识提供了新途径。由于非线性振动的一个主要特征是系统的固有频率和振幅有关，因此通过测量随时间变化的信号频率成分的变化情况可以实现对系统中非线性参数的识别。小波变换是一种信号的时间-尺度(与信号频率相对应)分析方法，在时域和频域同时具有表征信号局部特性的能力，非常适合进行时变和非线性振动系统的参数识别，因此，国内外对基于小波变换的非线性系统识别方法进行了一系列的研究：Staszewski[5]用Morlet小波变换对一个包含库仑阻尼和三次方刚度的系统进行了辨识。Ta等[6]利用平均法推导了单自由度弱非线性自由振动系统的的瞬时频率、解析幅度和解析幅度导数之间的理论函数关系，信号经Morlet小波变换后通过提取脊可以得到这三者的实际关系曲线，最后通过最小二乘曲线拟合即可估计系统的非线性阻尼和刚度系数，数值仿真表明该方法可以从弱非线性系统的自由振动响应中准确地辨识出库仑阻尼、平方阻尼和三次方刚度。任宜春等[7]用Morlet复小波函数对弱Duffing系统的有阻尼自由振动响应进行了辨识，得到系统的固有频率、阻尼系数和非线性系数。王超等[8]用连续小波变化的方法识别结构的非线性，基于Feldman提出的非线性结构骨架曲线概念，通过提取结构响应信号的小波脊和小波骨架，识别出结构的瞬时频率和瞬时幅值，得到非线性结构的骨架曲线，从而识别结构的非线性。Kitad[9]对具有非线性恢复力系统的剪切型结构的方程进行离散，利用小波的时间局部性将切线刚度用离散小波尺度函数表示，阻尼系数分段线性化，使振动微分方程变为以阻尼系数和小波尺度函数为变量的代数方程组，采用最小二乘法计算得到未知向量，进而确定阻尼系数和切线刚度，进一步识别了结构的滞回曲线，最终通过对一个多自由度系统的试验验证了该方法的有效性。

1 时变及典型非线性振动系统及其解

1.1 时变阻尼自由振动系统

时变阻尼系统的自由振动方程可以写为：

(1)

式中:ξ(t)为随时间变化的阻尼比；ω0为无阻尼固有圆频率。

在进行求解时，假定阻尼比在一个很短的时间内是慢变函数，则在这个短时间内可以看成是一个定常阻尼，此时方程(1)的解为

x(t)=A0e-ξω0tcos(ωdt+θ0)

(2)

式(1)中频率是不随时间变化的常数，瞬时振幅为

A(t)=A0e-ξω0t

(3)

可得

ln(A(t))=ln(A0)-ξω0t

(4)

1.2 达芬非线性振动系统

达芬有阻尼非线性自治方程为：

(5)

用Krylov-Bogoliubov平均法[10]进行求解，可得

(6)

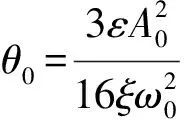
瞬时振幅和瞬时频率为

A(t)=A0e-ξω0t

(7a)

(7b)

达芬有阻尼非线性非自治方程为

(8)

由KBM法[10]，可得解为

(9)

式中的第一项为自由振动项，第二项为倍频项，第三项为简谐激励项。其中

A(t)=A0e-ξω0t

(10a)

(10b)

式中:A0和θ0分别为式(9)第一项的初始振幅和初始相位，同式(6)。

对比达芬有阻尼非线性自由振动响应可知，其简谐激励响应第一项的瞬时振幅、瞬时频率的表达式不变，而简谐激励振动响应为自由振动和简谐振动的叠加。

1.3 范德波尔非线性振动系统

范德波尔非线性自治方程为：

(11)

用Krylov-Bogoliubov平均法[10]进行求解，可得

(12)

式中:A0为初始振幅；相位为常数θ0。当t=0时，若已知初始振幅为A0，则可以由式(12)得θ0=0。

瞬时振幅和瞬时频率为

(13a)

ω(t)=ω0

(13b)

上式表明在一次近似精度范围内的计算结果对频率无修正，即相位不随时间变化。

范德波尔非线性非自治方程

(14)

由KBM法[10]，可得解为

(15)

式中

(16a)

φ=ω0t-θ0

(16b)

式中:A0为初始振幅。当t=0时，若振幅为A0，则此时θ0=0。

对比范德波尔非线性自由振动响应可知，其简谐激励响应第一项的瞬时振幅、瞬时频率的表达式不变，而简谐激励振动响应为自由振动和简谐振动的叠加。

2 小波变换法

2.1 小波变换的基本理论

设信号x(t) ∈L2(R)，基本小波或母小波函数ψ(t) ∈L2(R)，L2(R)表示平方可积的实数空间。若ψ(t)满足小波允许条件，则信号x(t)的连续小波变换定义为：

WTx(a,b)=x(t),ψab(t)=

(17)

小波变换的频域表示为：

(18)

任意实信号x(t)可以表示成如下时变振幅与时变相位的乘积形式：

x(t)=A(t)cosφ(t)

(19)

然而，这样的表示并不唯一，为保证表示的唯一性，通常引入其对应的解析信号：

(20)

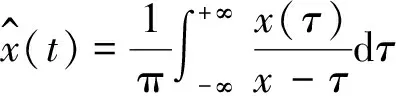
(21)

对于单一分量信号x(t)，其相应的复Morlet小波变换根据平稳相位原理可以得到[13]：

WTx(a,b)=x(t),ψab(t)z(t),ψab(t)=

(22)

式中：O(▯) 为二阶小量，可以忽略不计；φ(b)为小波变换的相位。

故小波系数的模和相位分别为：

(23a)

∠(WTx(a,b))=φ(b)

(23b)

信号的瞬时频率为：

(24)

小波系数的模反映了信号在时频平面上的能量密度分布，而信号的能量在时频平面上主要集中在脊线(每一时刻的频谱峰值连成的曲线)附近，因此可以由任一时刻的信号小波系数模的脊线点所对应的频域来确定瞬时频率。

由式(23a)可以看出，当小波尺度a满足条件：

(25)

小波系数模可取得局部极大值，相应的点(b,ar(b))称为小波脊点。连接时间-尺度平面上的相应脊点便构成小波脊线。

此时，脊线上的小波系数的模为：

(26)

由此，可由脊线上小波系数模求出瞬时振幅：

(27)

对于多分量信号x(t)，通常可将其表示成单一分量信号的叠加：

(28)

因为小波变换是线性变换，相应x(t)的小波变换可表示为：

(29)

通过选择合适的小波参数，可以将不同的单一信号分量在时间-尺度平面分离开来，从而分别提取各自小波脊，相应地得到信号瞬时频率。

2.2 连续Morlet小波变换

Morlet小波是一种单频复正弦调制高斯波，也是最常用的复值小波，其时、频两域都具有很好的局部性，它的时域、频域形式如下[14]：

时域ψ(t)=e-t2/2ejωct

(30a)

(30b)

ωc为中心频率，当ωc≥5 时，可认为Ψ(ω= 0) ≈0 近似满足容许性条件。

对于复解析小波Morlet 小波，频率f与尺度a之间的对应关系为：

(31)

其中:fs为信号的采样频率，*表示卷积运算[15]。

对于复Morlet 小波变换，其相应的时间分辨率和频率分辨率分别为[16]：

(32a)

(32b)

时间和频率分辨率满足不确定原理，增大小波中心频率ωc可以提高频率分辨率，但同时会降低时间分辨率，增加端点效应的影响。

3 数值算例

3.1 时变阻尼自由振动系统

算例：

具体步骤如下所示：

(1)用四阶龙格—库塔法计算非线性系统的振动响应，如图1所示，图中还给出了上下包络线。

图1 振动响应图

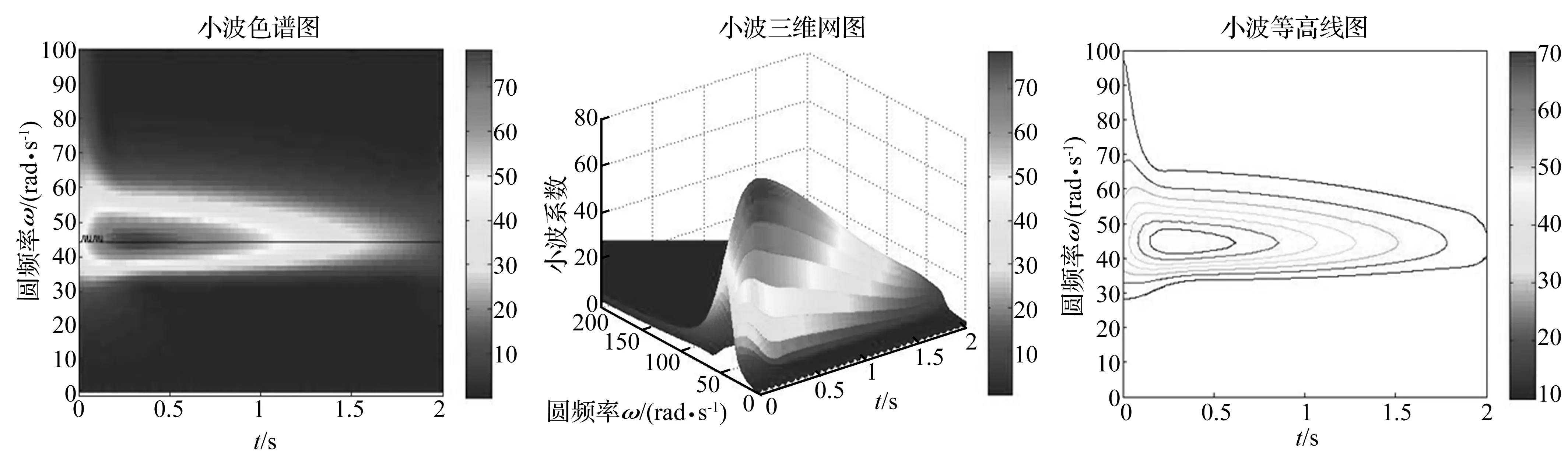
图2 小波色谱图

(2)用Morlet小波函数“cmor 2 - 1”对响应进行小波变换，得到色谱图、三维网图和等高线图分别如图2～4所示，图2中还画出了根据小波系数模的极大值确定的脊线。

(3)根据脊线可以得到瞬时频率如图5所示，为一常数，即ωd=44.44 rad·s-1，可近似取ω0=ωd。

(4)由脊线上的小波系数和式(27)可以求出瞬时振幅，如图6所示，图中还给出了由振动曲线图1得到的振幅包络线。另外，把瞬时振幅曲绘于图1中予以对比。

(5)图7给出了瞬时振幅的对数—ln(A(t))与时间t的关系曲线，剔除边端效应，取0.4 s～1.6 s的数据，对曲线求导可得曲线ξ(t)ω0，进而求得阻尼比随时间变化的曲线ξ(t)，如图8所示，图中还给出了拟合结果，ξ(t)=2.02×10-2t，以及理论结果ξ(t)=2×10-2t。

从以上分析可以看出，小波变换方法对时变阻尼自由振动系统的频率和瞬时阻尼比识别是有效的。

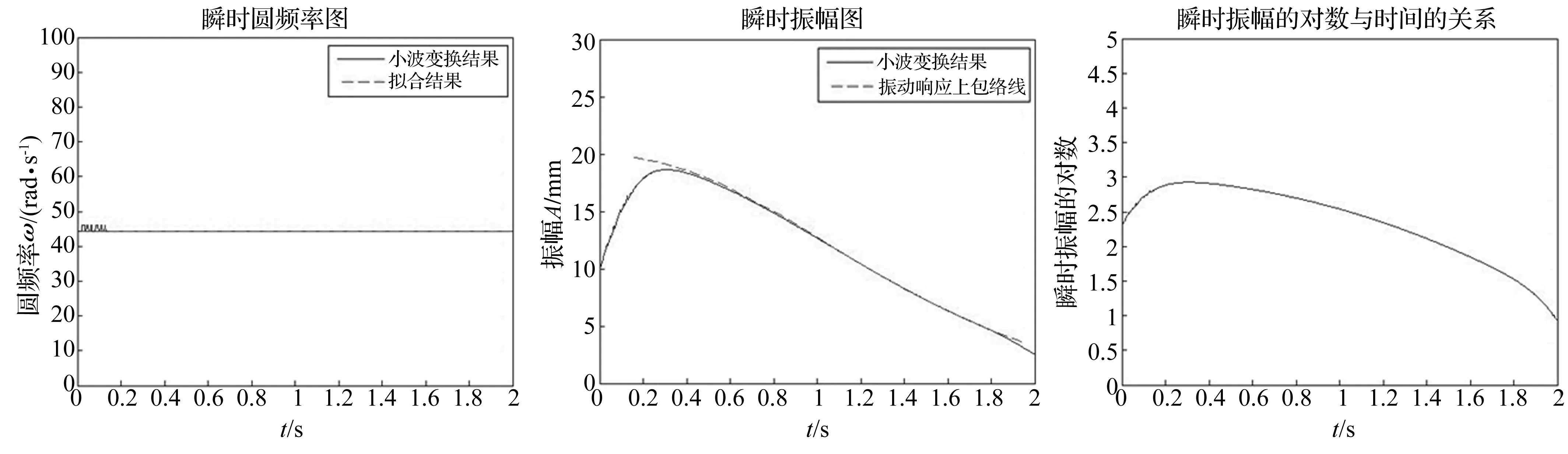
图5 瞬时圆频率图

图8 瞬时阻尼比图

3.2 达芬有阻尼非线性简谐激励振动系统

算例：

具体步骤如下所示：

(1)用四阶龙格-库塔法计算非线性系统的振动响应，如图9所示，图中还给出了根据KBM法的式(9)得到的振动响应，两者是非常接近的。

(2)用Morlet小波函数“cmor 2 - 1”对响应进行小波变换，得到色谱图、三维网图和等高线图分别如图10～12所示，图10中还画出了根据小波系数模的极大值确定的脊线。从图中可以看出，在1.2 s附近，简谐激励产生的振动能量开始大于初始位移引起的自由振动产生的能量，倍频项很小，可以忽略不计。

(3)根据图10的色谱图可知，振动主要由两个频率的振动叠加而成，对比式(9)就可以知道这两个频率形成的原因，因此分别在[0～100] rad·s-1和[100～200] rad·s-1两个频率段提取脊线，便可以得到瞬时频率如图13(a)和图13(b)所示，图13(a)中还给出了根据式(7b)得到的理论结果，图13(b)中还给出了ω的拟合结果和实际结果。从图中可以看出识别结果为ω=138.28 rad·s-1,与理论结果140 rad·s-1非常接近。

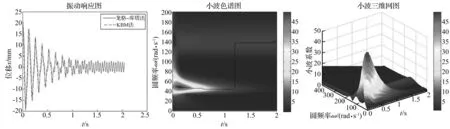
图9 振动响应图

图12 小波等高线图

(4)由脊线上的小波系数和式(27)可以求出在[0～100] rad·s-1频率段的瞬时振幅-即自由振动振幅，如图14(a)所示，图中还给出了根据式(7a)得到的理论结果。从图中可以看出，剔除边端效应，0.4 s～1.6 s的结果比较接近；由脊线上的小波系数和式(27)可以求出在[100～200] rad·s-1频率段的瞬时振幅—即受迫振动振幅，如图14(b)所示，图14(b)中还给出了拟合结果为2.283和根据公式(9)第3项计算的的理论结果为2.276，两者误差很小。

(5) 图15给出了瞬时振幅的对数-ln(A(t))与时间t的关系曲线，由式(7a)可得ln(A(t))=ln(A0)-ξω0，近似于线性关系，剔除边端效应，取0.4 s～1.6 s的数据，由最小二乘拟合可以得到ξω0=2.287 4和A0=19.85 mm。

图14 瞬时振幅图

(6) 图16给出了瞬时频率ω(t)与瞬时振幅A(t)平方—A2(t)的关系，剔除边端效应，近似于线性关系，取0.4 s～1.6 s的数据，由最小二乘拟合可以得到ω0=44.32 rad·s-1和ε=3.65，同时，根据步骤(5)的结果可以得到ξ=0.051 6。

图16 瞬时圆频率与瞬时振幅平方的关系图

从以上分析可以看出，小波变换方法对达芬有阻尼非线性简谐激励振动系统的固有频率和阻尼比、简谐激励频率和幅值、自由振动初始振幅等的识别精度是较高的，而对非线性参数的ε识别误差较大。

3.3 范德波尔非线性自由振动系统

算例：

具体步骤如下所示：

(1) 用四阶龙格-库塔法计算非线性系统的振动响应，如图17所示，图中还给出了根据平均法的式(13a)得到的振动响应，从图中可以看出，由于平均法只有一次近似精度，所以存在微小的相位差。

(2) 用Morlet小波函数“cmor 2 - 1” 对响应进行小波变换，得到谱图、三维网图和等高线图分别如图18～20所示，图18中还画出了根据小波系数模的极大值确定的脊线。

(3) 根据脊线便可以得到瞬时频率如图21所示，图中还给出了根据式(13b)得到的理论结果。已知频率为常数，剔除边端效应，取0.2 s～1.8 s的数据，直接进行最小二乘曲线拟合，便可以得到ω0=44.44(rad/s)，与理论值ω0=45(rad/s)非常接近。

(4)由脊线上的小波系数和式(27)可以求出瞬时振幅，如图22所示，图中还给出了根据式(13a)得到的理论结果。若已知公式(13a)，剔除边端效应，取0.2s～1.8s的数据，初始值ε、δ和A0分别取0.4、15和30，直接进行最小二乘曲线拟合，可以得到ε、δ和A0的拟合值分别为0.045、2.18和20.38。拟合结果和理论结果如图22所示。需要注意的是，由于用式(13a)进行拟合时要把3个参数当成未知数，因此拟合结果不唯一，与初始值的取值有很大的关系，并且剔除的数据不能太多，否则难以获得足够的信息。若把A0当作已知，则即使ε和δ的初始值取值不同，其拟合结果也较为稳定。

对于范德波尔非线性简谐激励振动系统的识别，可采用3.2节的类似的方法。

图17 振动响应图

图20 小波等高线图

4 结 论

本文用Morlet小波变换方法对时变振动系统和典型非线性振动系统进行参数识别，得出以下结论：

(1) 小波变换方法对时变阻尼自由振动系统的频率和瞬时阻尼比识别是有效的，并且可以达到较高的精度。

(2) 由于小波变换是线性变换，因此用小波变换方法可以分别获得达芬有阻尼非线性系统的自由振动和简谐激励振动，并对其分别识别。固有频率和阻尼比、简谐激励频率和幅值、自由振动初始振幅等的识别精度是较高的，而对非线性参数的ε识别误差较大。

(3) 在用小波变换方法对范德波尔有阻尼非线性自治方程进行识别时，由于边界效应的存在，会使得识别结果不够稳定，在应用最小二乘法进行曲线拟合时，初始值的取值对识别结果的影响很大。

(4) 鉴于以上的分析，小波变换边界效应的处理是下一步需要研究的方向，从而提高小波变换的识别精度，特别是对初值依赖性较强的情况。

[1] 于开平, 庞世伟, 赵婕. 时变线性/非线性结构参数识别及系统辨识方法研究进展[J]. 科学通报, 2009, 54: 3147-3156.

YU Kai-ping, PANG Shi-wei, ZHAO Jie. Advances in method of time-varying linear/nonlinear structural system identification and parameter estimate[J]. Chinese Sci Bull (Chinese Ver), 2009, 54: 3147-3156.

[2] 窦苏广, 叶敏气, 张伟卞. 基于增量谐波平衡的参激系统非线性识别法[J]. 力学学报, 2010,42(2):332-336.

DOU Su-guang, YE Min-qi, ZHANG Wei-bian. Nonlinearity system identification method with parametric excitation based on the incremental harmonic balance method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010,42(2):332-336.

[3] 张根辈, 臧朝平.基于振动测试的非线性参数识别方法 [J].振动与冲击,2013,32(1):83-89.

ZHANG Gen-bei, ZANG Chao-ping.A novel method for nonlinear parametric identification based on vibration tests[J].Journal of Vibration and Shock,2013,32(1):83-89.

[4] Jang T S. A method for simultaneous identification of the full nonlinear damping and the phase shift and amplitude of the external harmonic excitation in a forced nonlinear oscillator[J]. Computers and Structures, 2013, 120: 77-85.

[5] Staszewski W J. Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform[J]. Journal of Sound and Vibration, 1998,214(4):639-658.

[6] Ta M N, Lardies J. Identification of weak nonlinearities on damping and stiffness by the continuous wavelet transform[J]. Journal of Sound and Vibration, 2006,293(1-2):16-37.

[7] 任宜春，易伟建. 非线性系统识别的小波方法研究[J]. 振动与冲击，2007, 26 (3) : 68-71.

REN Yi-chun, YI Wei-jian. Identification of a nonlinear system using wavelet transformation[J]. Journal of Vibration and Shock,2007,26(3):68-71.

[8] 王超，任伟新，黄天立. 基于小波的非线性结构系统识别[J]. 振动与冲击, 2009, 28 (3) : 10-14.

WANG Chao, REN Wei-xin, HUANG Tian-li. System identification of a non linear structure based on wavelet transformation[J]. Journal of Vibration and Shock, 2009,28(3):10-14.

[9] Kitada Y. Identification of nonlinear structural dynamic systems using wavelet[J]. Journal of Engineering Mechanics, 1998, 124: 1059-1066.

[10] 刘延柱，陈立群. 非线性振动[M]. 北京：高等教育出版社，2001.

[11] 陈逢时. 子波变换理论及其在信号处理中的应用[M]. 北京: 国防工业出版社, 1998.

[12] Cohen L. Time-frequency analysis [M]. New Jersey: Prentice Hall, 1995.

[13] Delprat N, Escudie B, Guillemain P, et al. Asymptotic wavelet and gabor analysis: extraction of instantaneous frequencies[J]. IEEE Transactions on Information Theory, 1992, 38(2): 644-644.

[14] 任伟新，韩建刚，孙增寿. 小波分析在土木工程结构中的应用[M]. 北京：中国铁道出版社，2006

[15] Ruzzene M, Fasana A, Garibaldi, et al. Natural frequencies and dampings identification using wavelet transform: application to real data [J]. Mechanical Systems and Signal Processing, 1997, 11(2): 207-218.

[16] Kijewski T, Kareem A. Wavelet transforms for system Kijewski T, Kareem A. Wavelet transforms for system identification in civil engineering [J]. Journal of Computer-Aided Civil and Infrastructure Engineering, 2003, 18(5): 339-355.