非线性常微分方程高阶谐波平衡法傅里叶展开的简化

唐元璋,翁雪涛，楼京俊，林雄伟，张晖

（1.海军工程大学动力工程学院，武汉430033；2.船舶振动噪声重点实验室，武汉430033）

非线性常微分方程高阶谐波平衡法傅里叶展开的简化

唐元璋1,2,翁雪涛1,2，楼京俊1,2，林雄伟1,2，张晖1,2

（1.海军工程大学动力工程学院，武汉430033；2.船舶振动噪声重点实验室，武汉430033）

简化了一种求取非线性常微分方程高阶谐波解的近似解析计算方法。对平方和立方非线性项的傅里叶展开过程进行改进和简化，使计算过程变为两次矩阵运算即可完成展开过程，且两次矩阵运算过程一致，易于编程。以Duffing方程为算例，计算结果与数值方法一致，运算效率有所提高。

振动与波；非线性常微分方程；Duffing方程；傅立叶展开；谐波平衡法

线性隔振系统存在共振难避免等问题[1，2]。因此学者们对非线性隔振器开展了研究[3，4]，但与线性隔振系统相比，非线性隔振系统的响应复杂得多。很多非线性振动系统可以简化为单自由度质点与非线性弹簧组合的振动系统，这类系统的动力学方程即为非线性常微分方程。图1所示的系统动力学方程无量纲化后称为Duffing方程[5]。研究非线性常微分方程的主要方法包括解析方法和数值方法，数值方法只能得到解的时间序列，不能直接得到周期解各谐波分量的幅值与系统各参数之间的变化关系，所以解析方法仍然是重要的研究方法。非线性常微分方程的精确解析解大多无法求解，这里的解析方法主要是指近似解析方法，求解非线性常微分方程的近似解析方法有谐波平衡法、摄动法、平均法、多尺度法和渐进法等[6，7]。各种近似解析方法中，谐波平衡法概念最简单明了，且适用于强非线性系统，基本思想是将振动系统的激励项和方程的解都展开成傅立叶级数，为了保证系统的作用力和惯性力的各阶谐波分量自相平衡，必须令动力学方程两端的同阶谐波的系数相等，从而得到包含未知系数的一系列代数方程，以确定待定的傅立叶级数的系数。谐波平衡法解非线性常微分方程的过程就是确定待定的傅立叶级数的系数的过程。

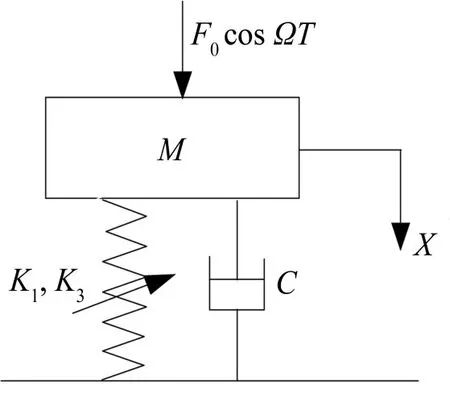
图1 非线性隔振系统

应用谐波平衡法是假设非线性常微分方程的解只包含一个谐波[8，9]，本文简称单一谐波解，这在研究共振时是有效的，但非共振情况下其他谐波项不能忽略，这需要研究高阶谐波解，而对于高阶谐波解的研究很少涉及[10，12]，而单一谐波或谐波个数较少，则无法求得高精度的解；如果非线性常微分方程包含平方项和立方项，计算高阶谐波解的傅立叶级数系数时需将其展开，当谐波阶数超过5时，这个展开过程如果用直接积分的方法，将产生很大的计算量，计算机难以计算。为了减少积分运算，Kawakami[13]等用求取偏导数的方法计算平方项和立方项傅里叶展开过程，但计算过程较为复杂；Ameer Hassan[14]用到一种直接展开计算的高阶谐波平衡法，沈建和[15]等研究了类似的计算方法。这些方法，计算过程较为复杂，不利于编程实现。本文改进了一种针对谐波平衡法傅里叶系数展开的计算方法，力求简化过程，使得计算平方项和立方项的展开过程统一，便于编程实现，也易于扩展到计算其它类型非线性项的傅里叶展开。这一改进的傅里叶展开计算过程不仅可以在谐波平衡法中应用，也可以应用到椭圆函数谐波平衡法[16]、增量谐波平衡法中[17]。为了检验本文计算方法的正确性和有效性，对Duffing方程进行了求解计算，并与数值方法做了对比。

1 计算过程

1.1 高阶谐波平衡法的求解过程

第一步：将解设为傅立叶级数的解。设它的周期解为傅立叶级数形式

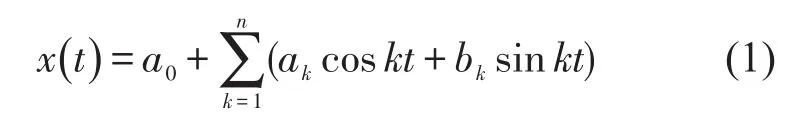
式(2)中Fc0，Fck，Fsk是包含a0，ak，bk的多项式，其中k=1,2,3…∞。根据傅立叶级数系数的定义，定义P为求傅立叶级数系数的运算，P与Fc0，Fck，Fsk有如下关系

第三步：列出包含未知系数的代数方程组。由(2)式可得Fc0=0，Fck=0，Fsk=0即

其中k=1,2,3…n,k取有限项即为近似解。这样根据三角级数的正交性和式（1）—（8）可列出2n+1个方程。

第四步：解方程组。当n很小（n≤2）可求取幅值与频率之间的解析关系，当n很大时则只能用数值方法得到半数值半解析解，方程组（6）—（8）是2n+1个方程组成的，可用牛顿法或其他数值算法[18，19]解得各系数a0,a1…ak,b1…bk。

1.2 多项式函数的Fourier展开

为了列出1.1节第三步的代数方程组，如果直接按式(3)，(4)，(5)直接积分求解，那么计算量将非常大，n≥5时用Mathematica计算消耗内存很大而无法运算。如设更高阶谐波则很难计算。为了减少计算量，本文对多项式函数Fourier展开法进行了改进，使得过程简单，易于理解和编程实现。设非线性常微分方程的近似解为有限项的傅立叶级数

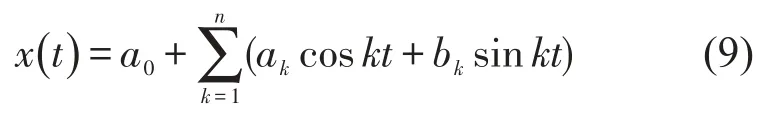
n为式（9）中包含的谐波阶数。c0,ck,dk是包含a0,ak,bk的多项式。利用式(6)，(7)，(8)可以求取c0,ck,dk与a0,ak,bk的关系。为了简化计算过程，改用矩阵计算，这样也便于编程计算。设

c中共有4n+1项。则x(t)可表示为式（13）

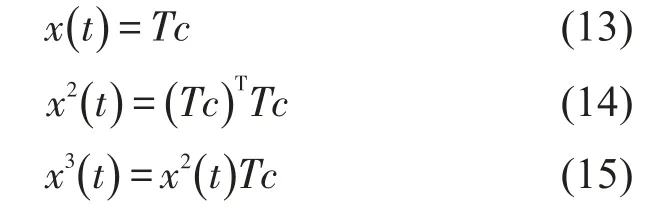
定义矩阵

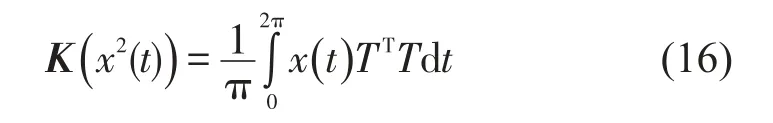
则有

根据式（17）可以很快得到x2(t)的傅立叶系数Pc0(x2(t))，Pck(x2(t))，Psk(x2(t))，也就是c0，ck，dk其中(k=1，2，3…2n)。

要求K(x2(t))，首先得研究TTT矩阵，计算这个矩阵等价于x2(t)的展开过程。

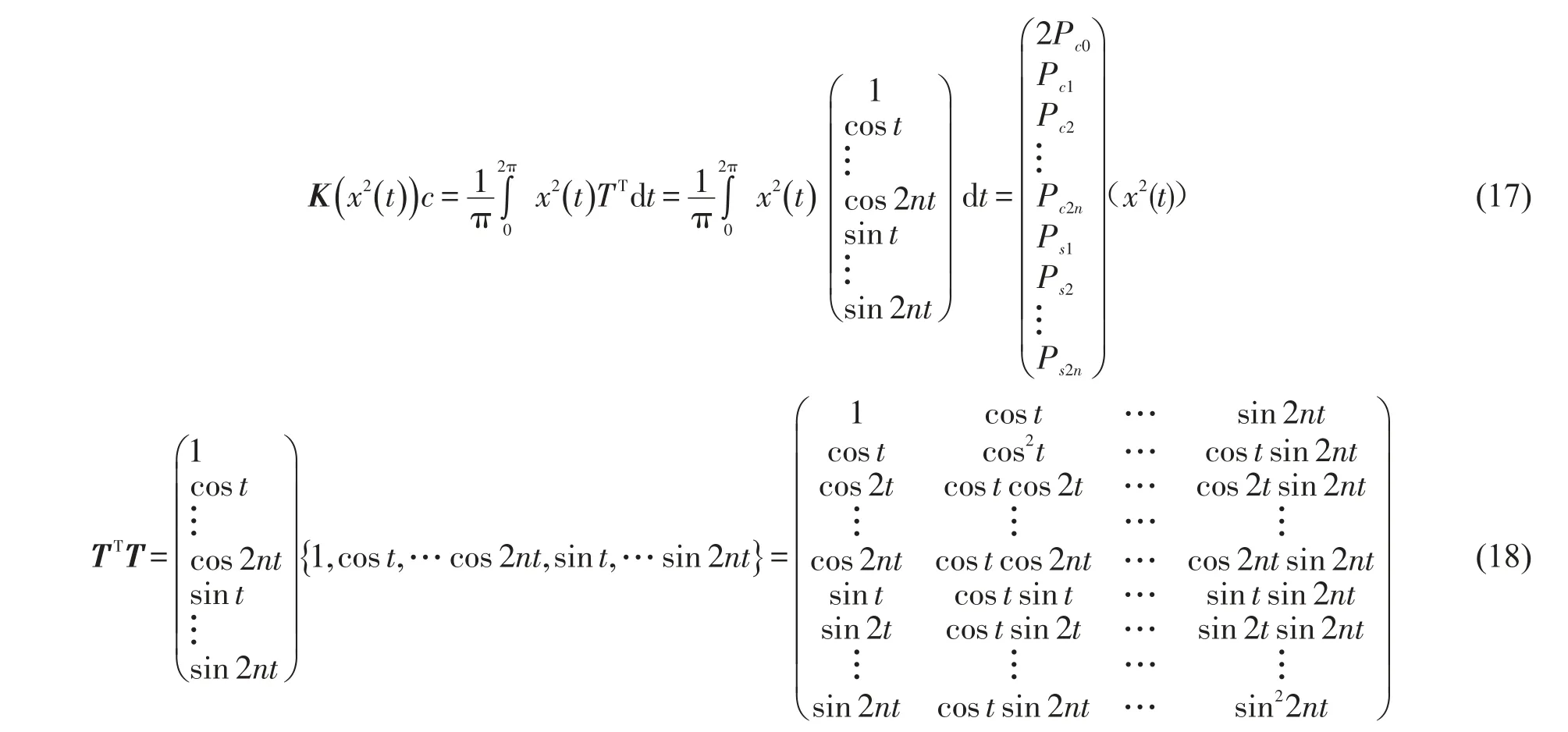
根据TTT的特点，利用三角级数正交性和积化和差公式即可计算K(x2(t))，用K(x2(t))[i，j]表示第i行j列。其中i,j=1，3…2n，各矩阵元素计算如下

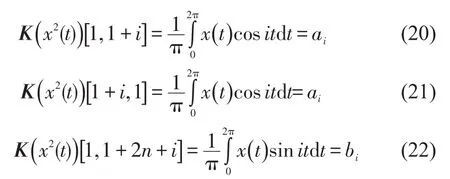
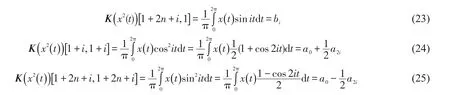
当i≠j时

其中Sign[]和Abs[]分别为取符号运算和取绝对值运算

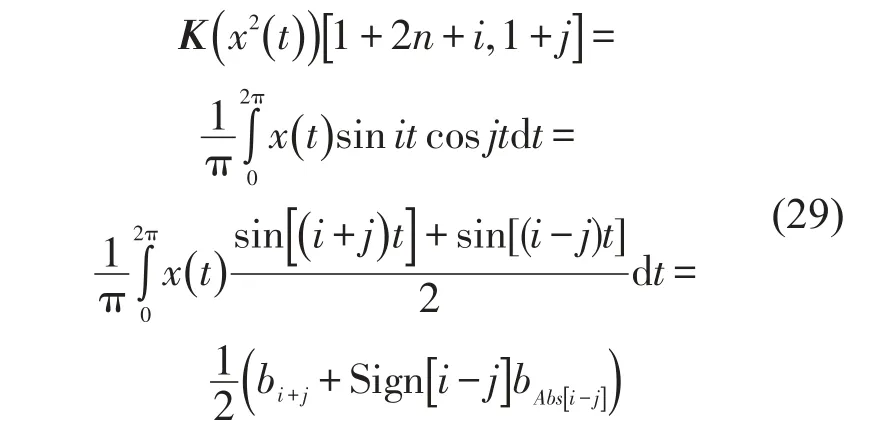
类似地x3(t)的傅立叶系数P(x3(t))也可求出，但因为只需列出2n+1个方程，不必计算出全部P(x3(t))，所以另设

其中T1和c1只包含2n+1项

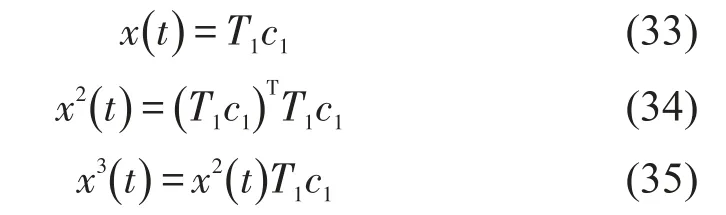
定义矩阵

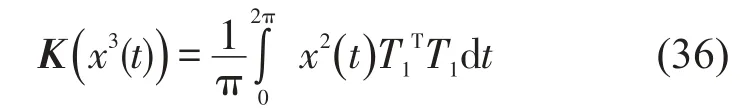
则有

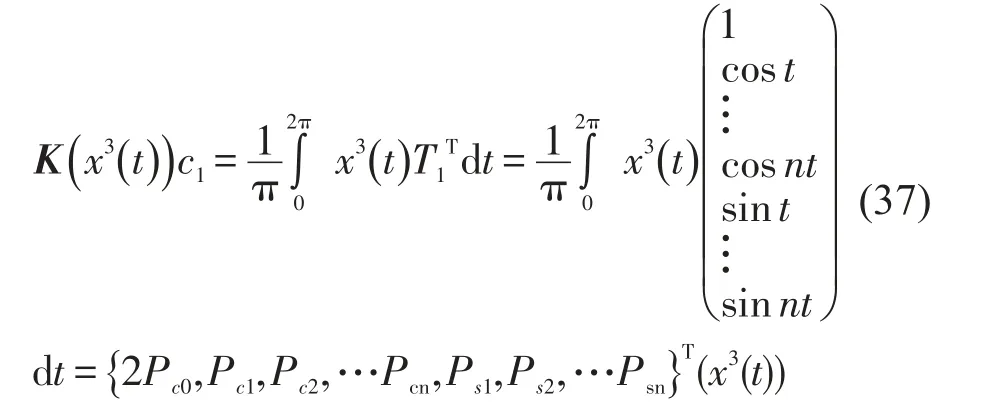
根据式（37）可以得到x3(t)的傅立叶系数Pc0(x3(t)),Pck(x3(t)),Psk(x3(t)),也就是e0,ek,fk,其中k=1,2,3…n。若要计算x3(t)全部的系数则将T1和c1设为6n+1项即可。

类似地可以得到以下结论

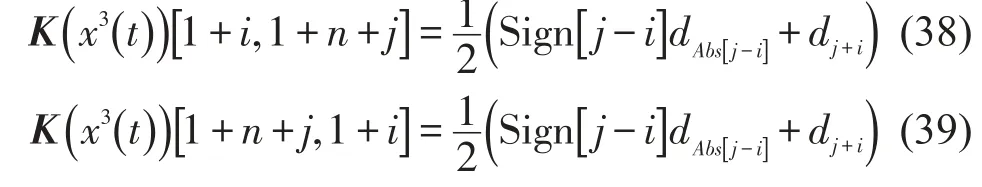
当i≠j时

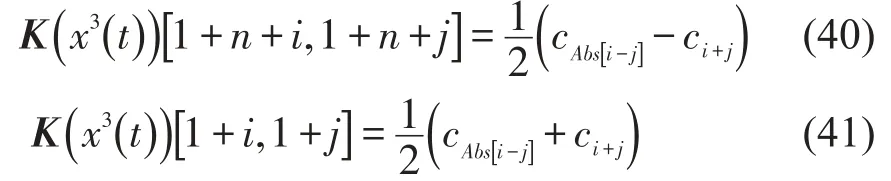
当i=j时

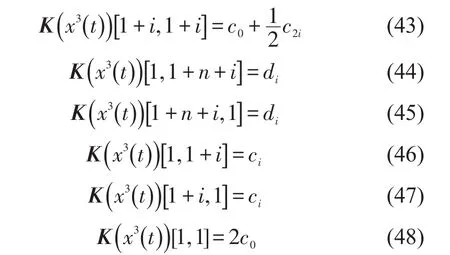
综上所述，Pc0(x3(t)),Pck(x3(t)),Psk(x3(t))即x3(t)的傅立叶系数e0,ek,fk可由K(x3(t)) c1得到e0,ek,fk与c0,ck,dk的关系；由K(x2(t)) c可得到c0,ck,dk与a0,ak,bk的关系。只需要通过两次矩阵运算就可就求得Pc0(x3(t)),Pck(x3(t)),Psk(x3(t))。这样通过式(6)，(7)，(8)可以很容易得到2n+1个方程。

1.3 总结计算过程

整个计算过程总结为两次矩阵运算和解方程组运算。

1.4 误差

这里的误差只讨论近似解析解的计算误差，因精确解尚无法求得，近似解析解与精确解的误差对比不做讨论。计算误差来源于两方面，一是牛顿法的计算误差E1，可以通过增加迭代次数来减小误差。

二是截断误差，所设谐波解仅为有限项n,多项式最高次项xm()t展开后最多有mn项，利用e0,ek, fk可求得截断误差E2。为了求出全部的系数只需将1.2节中T1和c1设为包含2mn+1项即可

总误差为

2 算例

2.1 计算周期解

硬弹簧Duffing振子[1，20]是非线性振动模型的典型代表，它的动力学方程经无量纲化后为

式（52）是一个多项式非线性方程，称为Duffing方程，式中δ为阻尼率，α1和α3分别为线性项系数和立方非线性项系数，A为激励力，ω激励频率,φ为相位；分别为加速度、速度、位移，以上各参数均为量纲为1的量。

联合式（1）—（8）及式（52）很快可以得到方程组

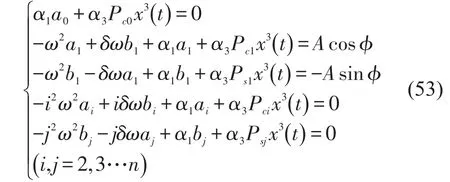
固定一组参数进行运算，令α1=1，α3=1，A=1，φ=0，ω=0.9，δ=0.1。将谐波阶数n设定为30进行运算,得到结果是高阶谐波近似解析解的傅立叶系数，列于表1。

为了验证计算方法的正确性，与数值计算方法进行对比，如图2所示，实线表示数值计算的结果，实点表示本文方法，本文称之为矩阵方法。两种计算方法所得的结果是一致的。

2.2 误差分析

按1.4节的定义计算误差，各参数不变，只改变所设近似解析解的谐波阶数。表2表明随着谐波阶数的增加，E1和E2都会下降，当n=30时，E2＜＜E1这说明计算方法的精度是足够的。

2.3 运算效率分析

本文方法是将谐波平衡法的傅里叶展开过程整理成两次矩阵运算，非常适合在Matlab软件中计算[21]，减少了代码语句，如表3所示，运算效率有一定的提高。

图2 矩阵方法与数值方法的对比

表1 高阶谐波解的傅立叶系数

表2 误差分析

表3 运算时间比较

3 结语

总结了多种近似解析方法后，针对带有平方项和立方项的非线性常微分方程，简化和改进了一种高阶谐波平衡法。这种计算方法仅包含两次矩阵运算和一次解方程组运算，两次矩阵运算的过程一致，步骤简单，可以方便地进行编程计算。本文的主要工作包括：

（1）与多种近似解析方法相比，为了求得非线性常微分方程周期解的高阶近似解析解，选用谐波平衡法是最简单有效的方法。将谐波平衡法求解非线性常微分方程的一般过程进行了分解，将过程归结为先设解为傅里叶级数形式并代入微分方程，经过谐波平衡得到傅里叶系数方程组，最后求解方程组；

（2）对非线性项的傅里叶展开过程进行了改进，把多个运算步骤归结为两次计算过程统一的矩阵运算，使程序的编写变得简洁，运算比Ameer Hassan的方法更高效。

（3）非线性项的傅里叶展开计算结果与数值方法一致；误差分析表明算法的精度主要依赖于谐波阶数的选取。

[1]楼京俊.基于混沌理论的线谱控制技术研究［D］.武汉：海军工程大学，2006.

[2]徐道临，吕永建，周加喜.非线性隔振系统动力学特性分析的FFT多谐波平衡法[J].振动与冲击，2012，31（22）：39-44.

[3]曹利，冯奇，张乐乐.双非线性隔振器的双层隔振系统模型的建立[J].噪声与振动控制，2008，28（2）：1-3.

[4]路纯红，白鸿柏，杨建春.超低频非线性隔振系统的研究[J].噪声与振动控制，2010，30（4）：10-12.

[5]G.Duffing.Erzwungene Schwingungen bei veränderlicher EigenfrequenzundihretechnischeBedeutung[M].Braunschweig,Vieweg&Sohn,1918.

[6]刘延柱，陈立群.非线性振动[M].北京：高等教育出版社，2001.

[7]刘式适，刘式达.物理学中的非线性方程[M].北京：北京大学出版社，2000.

[8]王本利，张相盟，卫洪涛.基于谐波平衡法的含Iwan模型干摩擦振子非线性振动[J].航空动力学报，2013，28（1）：1-9.

[9]吕永建.FFT多谐波平衡法及其应用[D].长沙：湖南大学，2012.

[10]Lau S L,Cheung Y K.Amplitude incremental variational principle for non-linear vibration of elastic systems[J].ASME,Journal of Applied Mechanics,1981:48:959-964.

[11]Mickens R E.An introduction to nonlinear oscillations [M].Cambridge University Press，Cambridge，1981.

[12]Hamdan M N,Burton T D.On the steady state response and stability of non-linear oscillators using harmonic balance[J].Journal of Sound and Vibration，1993，166 (2):255-266.

[13]Kawakami,Kobayashi.Computationofperiodic solutionsforpolynomialnonlinearequations[J].Electronics&Communications in Japan,1981,64-A(8): 7-14.

[14]Ameer Hassan.On the periodic and chaotic responses of duffing’s oscillator[D].Washington:Washington state university,1989.

[15]沈建和.非线性振动系统的分岔、混沌及相关控制[D]．广州：中山大学，2008.

[16]钮耀斌，王中伟.基于椭圆函数谐波平衡法的二元机翼非线性颤振[J].工程力学，2013，30（4）：461-465.

[17]晏致涛，张海峰，李正良.基于增量谐波平衡法的覆冰输电线舞动分析[J].振动工程学报，2012，25（2）：161-166.

[18]何汉林，梅家斌.数值分析[M].北京：科学出版社，2007.

[19]李厚儒，南敬昌.拟牛顿粒子群算法在非线性电路谐波平衡方程中的应用[J].计算机应用与软件，2013，30（2）：103-105.

[20]李晓勇.基于强Duffing模型的隔振装置混沌特性参数研究[D].广州：广州大学，2011.

[21]薛定宇，陈阳泉.高等应用学习问题的MATLAB求解[M].北京：清华大学出版社，2004.

Simplification of Fourier Expansion in the High-order Harmonic Balance Method for Nonlinear Ordinary Differential Equations

TANG Yuan-zhang,WENG Xue-tao, LOU Jing-jun,LIN Xiong-wei,ZHANGHui

(1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China; 2.National Key Laboratory on Ship’s Vibration&Noise,Wuhan 430033,China)

A simplified computation method of the high-order harmonic solution for nonlinear ordinary differential equations is discussed.Fourier expansion procedure of the equation with quadratic or cubic terms is improved and simplified.The procedure consists of two steps of matrix operation with the same computation process so that the algorithm is easier to program than that of the previous equation.Results of the solution for the Duffing equation using this method show that the high-order harmonic solution is in good agreement with its numerical solution,but more efficient than the latter one.

vibration and wave;nonlinear ordinary differential equation;Duffing equation;Fourier expansion; harmonic balance method

O175.14

ADOI编码：10.3969/j.issn.1006-1335.2014.02.007

1006-1355(2014)02-0028-06

2013-07-09

国家自然科学基金青年基金资助项目（基金编号：51009143）；

高等学校全国优秀博士学位论文作者专项资金资助项目（基金编号：201057）

唐元璋（1985-），男，湖南湘潭人，硕士，从事非线性动力学、振动与噪声控制研究。

E-mail:417006772@qq.com