一个新四维混沌系统的分岔分析

杜文举，俞建宁，张建刚，安新磊

（兰州交通大学数理学院，甘肃 兰州 730070）

18世纪以来，科学家对天体力学、流体力学和非线性振动中的一些失稳现象的研究发现了分岔现象.对于含参数的系统，当参数变动并经过某些临界值时，系统的拓扑结构发生本质的变化，我们称这种变化为分岔.Hopf分岔是一类比较简单但很重要的动态分岔问题.它不仅在动态分岔研究和极限环研究中有着重要的理论价值，而且它密切联系着自激振动产生的问题，所以在解决实际问题中也有着很广泛的应用.随着人们对分岔现象的研究，分岔理论已经取得了很大研究成果.文献［1］讨论了一个混沌系统的霍普夫分岔情况，并通过计算系统的第一Lyapunov系数，判断了其分岔的方向，对相应的动力系统行为也做了简要的分析.文献［2］研究了一个类Lorenz系统，详细讨论了该系统的稳定性，运用第一Lyapunov系数法分析系统平衡点的Hopf分岔情况.文献［3］通过严格的数学推导及数值仿真研究了一个新的类Lorenz系统，得到了平衡点稳定性及Hopf分岔的参数条件，通过对系统的第一Lyapunov系数的分析，推导出系统发生余维二退化Hopf分岔的参数条件.文献［4］提出了一个新的三维自治类Lorenz系统，理论分析了该系统的动力学特性，并通过数值计算分析了系统在平衡点处的稳定性，以及产生Hopf分岔的条件.目前已经有很多关于这方面的文献和专著［5－14］，文献［5］基于一个三维混沌系统构造了一个新的四维超混沌系统，并分析了该系统平衡点的稳定性、吸引子的相图、系统的分岔图和Lyapunov指数谱等基本动力学特性.然而，文献［5］并未对系统的Hopf分岔进行研究，本文将通过中心流形理论和范式理论，对该系统的Hopf分岔行为进行详细研究.

1 新的四维混沌系统

文献［5］提出了一个新的四维自治混沌系统，其状态方程为：

其中：x＝（x，y，z，u）T∈R4为系统的状态变量；a，b，c，m 是实参数.当参数a＝20，b＝35，c＝5，m＝4时，系统（1）存在一个混沌吸引子，如图1所示.

图1 系统（1）在不同空间的吸引子

本文采用 Wolf算法，计算得到系统（1）的4个Lyapunov指数：λ1＝0.3477，λ2＝0.1983，λ3＝0，λ4＝－26.4303.并由Kaplan－Yorke猜想公式，求得Lyapunov维数DKY＝3.02065.系统（1）的时间响应图、庞加莱截面、Lyapunov指数谱图及其功率谱图如图2所示.

图2 系统（1）得到的各种谱图

2 平衡点稳定性分析

令方程组（1）的右边等于零，即

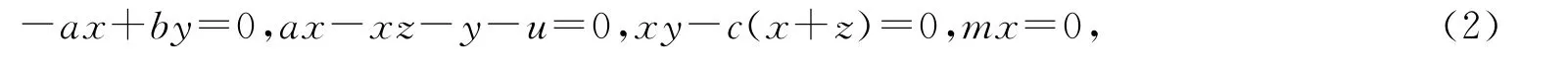
可以解得系统有唯一的平衡点E0＝（0，0，0，0）.

定理1 如果a＞－1，mb＞0，a（1－b）＞0，c＞0且

这时，平衡点E0渐近稳定.

证明 系统（1）在平衡点E0＝（0，0，0，0）处的Jacobian矩阵为

求得系统（1）在平衡点E0处Jacobian矩阵的特征方程为

根据Routh－Hurwitz判据，可知方程（5）的一切根的实部为负数的必要且充分条件是不等式

成立.所以，当满足以上条件时，平衡点E0渐近稳定.

定理2 如果方程（5）有一对纯虚根λ1，2＝±iω0，并且Re（λ′m（m0））≠0.若有a＞0，b＜0，c＞0，当m穿过临界值m0时，系统（1）在平衡点E0发生Hopf分岔.

证明 令λ＝iω（ω＞0）为方程（5）的根，则有

分离以上方程的实部和虚部，通过计算有

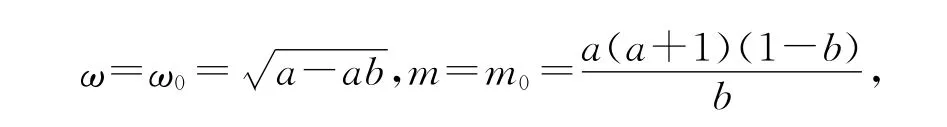
方程（4）的4个特征值为：

对方程（4）两边同时关于m求导，有

根据上式可得

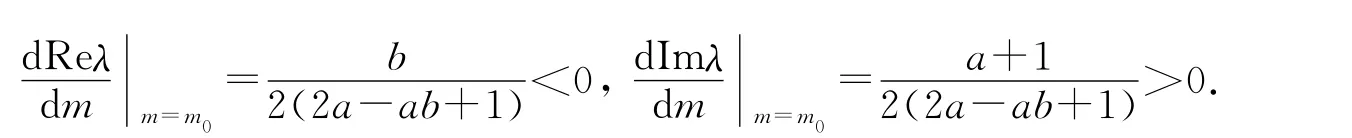
根据文献［6］中的Hopf分岔理论，可知m0便是分岔的临界值.假设a＞0，b＜0，c＞0，当m穿过临界值m0时，系统（1）在平衡点E0发生Hopf分岔.

3 平衡点E0的Hopf分岔分析

在理论分析之前，我们先回顾一下文献［7］中介绍的对于四维系统Hopf分岔的第一Lyapunov系数的求法.

考虑如下系统

其中x∈R4，ζ∈Rm分别是系统的状态变量和控制参数.假设系统（7）有一个平衡点x＝x0，ζ＝ζ0，并且变量x－x0仍然记做x，则F（x）＝f（x，ζ0）的泰勒展开式为

其中A＝fx（0，ζ0），并且对i＝1，2，3，4有

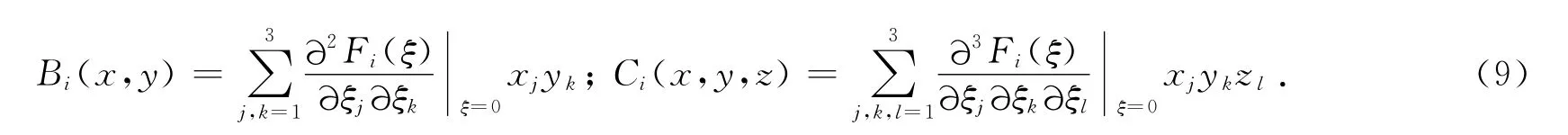
假设在平衡点（x0，ζ0）系统（7）的Jacobian矩阵有一对纯虚根λ2，3＝±iω0（ω0＞0），并且其他的特征值没有零实部.

令p，q∈C4满足

其中AT为A的转置.则第一Lyapunov系数可以定义为

其中：

I4为4×4的单位矩阵.

当a＞0，b＜0，c＞0，m＝m0时，我们讨论平衡点E0处的Hopf分岔.根据（9）式，可以计算得对应于f的线性函数

通过直接的计算可以求得满足（10）式的特征向量

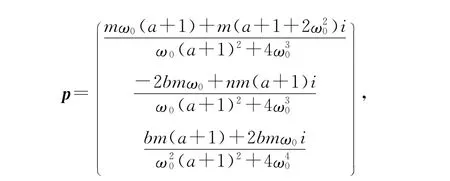
并且有

其中：

同样可以得到

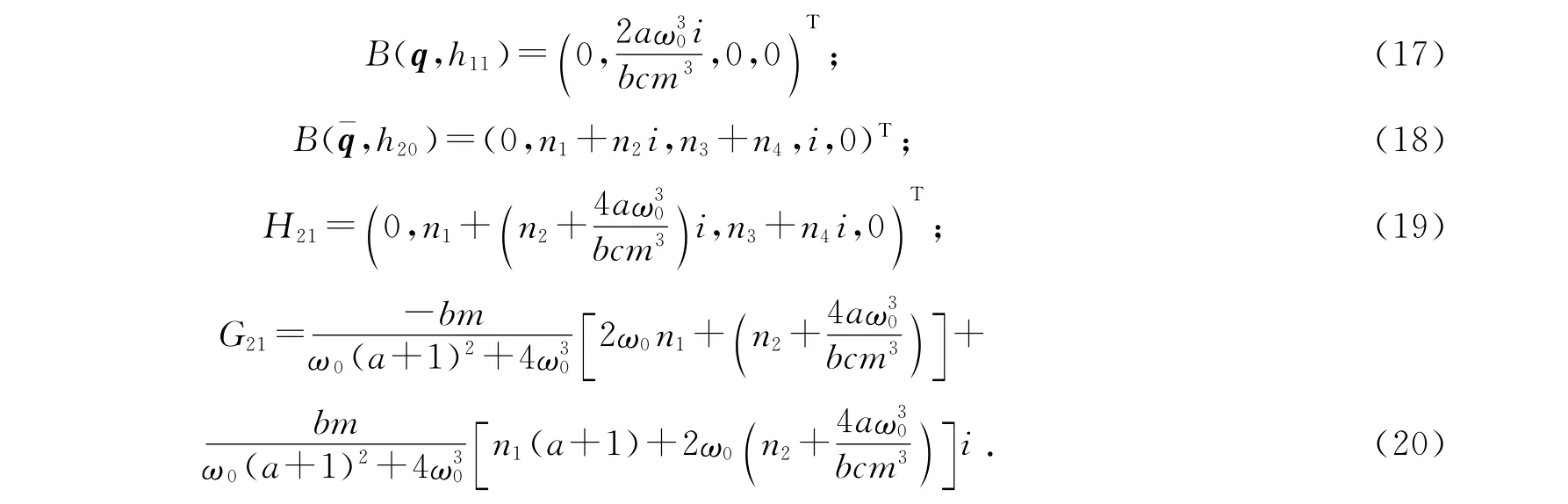
其中：

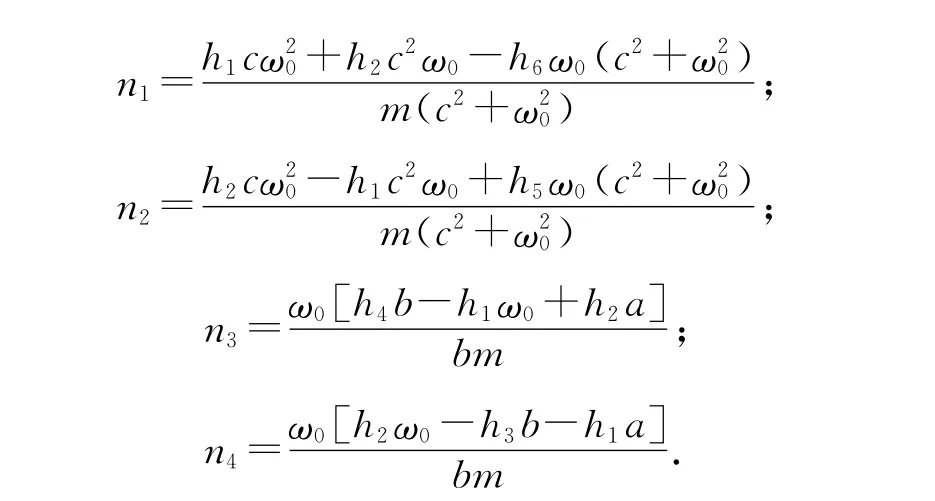
定理3 系统（1）在平衡点E0处的第一Lyapunov系数为

如果l1≠0，则此时系统（1）在平衡点E0处发生非退化的Hopf分岔.如果l1＝0，则系统（1）在平衡点E0处发生余维二的Bautin分岔.

4 数值仿真

为了验证以上的理论分析，我们选取一组参数：a＝2，b＝－1，可以得到Hopf的临界值m0＝－12.当m＝－10＞m0时，平衡点是稳定的；当m＝－14＜m0时，平衡点是不稳定的，分别如图3—5所示.根据前面的结论，并且经过复杂的计算得到l1＝－0.362681＜0，则系统（1）在平衡点E0的Hopf分岔是超临界的Hopf分岔，并且产生一个稳定的极限环.

当固定参数a＝20，b＝35，m＝4，参数c∈［0，1］变化时，系统（1）的Lyapunov指数谱和关于x的分岔图如图6所示.随着c的不断变化，系统的Lyapunov指数在变化，系统的状态也在跟着发生改变.当c∈（0，0.18）时，系统（1）处于拟周期运动状态.当c∈（0.18，0.4）时，系统（1）处于周期运动状态.当c∈（0.4，1）时，系统处于混沌状态.

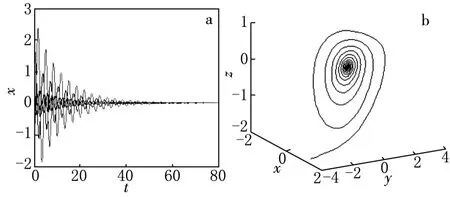
图3 当a＝2，b＝－1，c＝5，m＝－10时，系统（1）的时间响应图（a）和相图（b）

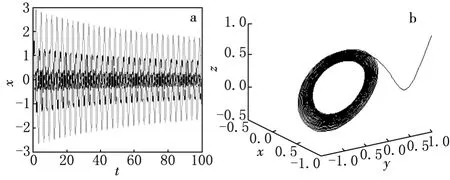
图4 当a＝2，b＝－1，c＝5，m＝－12时，系统（1）的时间响应图（a）和相图（b）

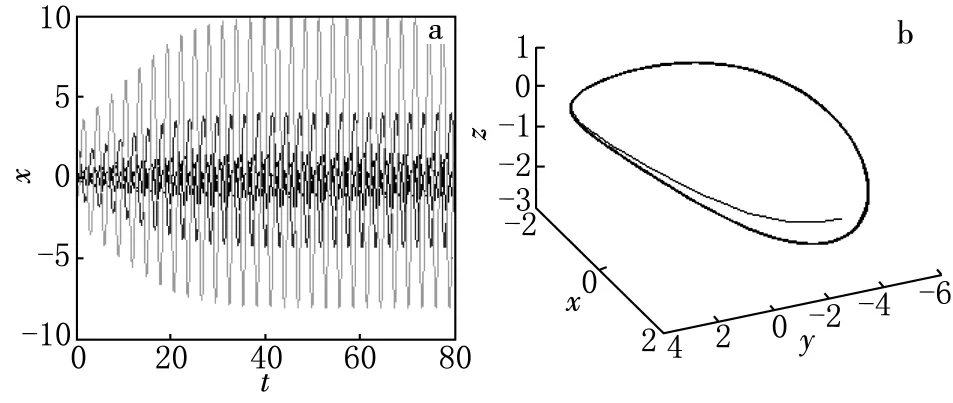
图5 当a＝2，b＝－1，c＝5，m＝－14时，系统（1）的时间响应图（a）和相图（b）

图6 参数c变化时系统（1）关于x的分岔图（a）和Lyapunov指数谱图（b）

当固定参数a＝20，b＝35，c＝5，参数m∈［50，70］变化时，系统（1）的Lyapunov指数谱和关于x的分岔图如图7所示.当m∈（50，55）时，系统（1）处于混沌状态；当m∈（55，55.8）时，系统（1）处于周期运动状态；当m∈（55.8，57）时，系统又近于混沌状态；当m∈（57.59.5）时，系统处于四周期运动状态；当m∈（59.5，66）时，系统处于二周期运动状态；当m∈（66，70）时，系统处于一周期运动状态.当m取不同值时，系统（1）的相图如图8所示.

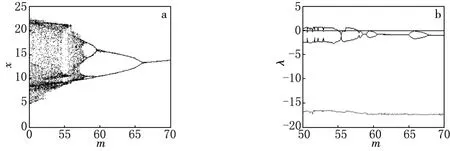
图7 参数m变化时系统（1）关于x的分岔图（a）和Lyapunov指数谱图（b）

固定a＝20，c＝5，系统（1）在平衡点E0的特征多项式为

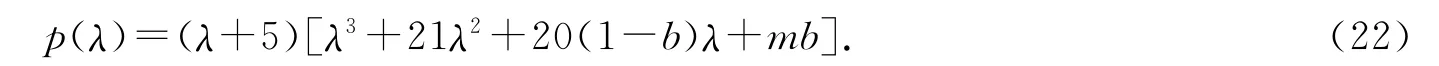
当b＜1，mb＞0，420（1－b）＞mb时，平衡点E0渐近稳定；当b＜1，mb＞0，420（1－b）＝mb时，满足Hopf分岔发生的参数条件.令b＝1，mb＝0，420（1－b）－mb＝0，画出b－m参数空间上平衡点的稳定域，如图9所示.其中曲线Li，i＝2，3，4分别代表b＝1，mb＝0和420（1－b）－mb＝0，在曲线L4上满足 Hopf分岔发生的参数条件.区域（Ⅰ）：b＜1，mb＞0，420（1－b）＞mb，在区域（Ⅰ）上平衡点E0渐近稳定，其他区域平衡点E0都不稳定.结合图9，取b＝－8，则它与L4相交点即为Hopf分岔点，可以求得分岔临界值m0＝－472.5.此时，系统发生Hopf分岔有一个极限环产生，如图10b所示.图10a，c和d分别为取区域（Ⅰ）、区域（Ⅷ）和区域（Ⅵ）中的点所得到的相图，与图1的理论分析相符合.

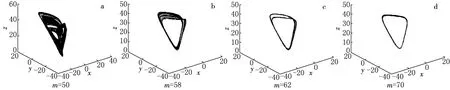
图8 m取不同值时系统（1）的相图

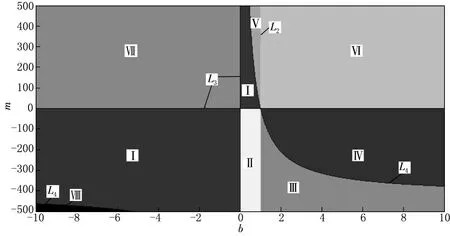
图9 系统（1）在参数平面（b，m）上的稳定域

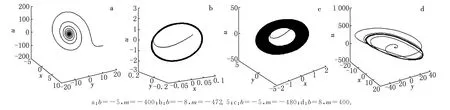
图10 系统（1）在b和m不同参数下的相图

固定b＝35，c＝5，系统（1）在平衡点E0的特征多项式为

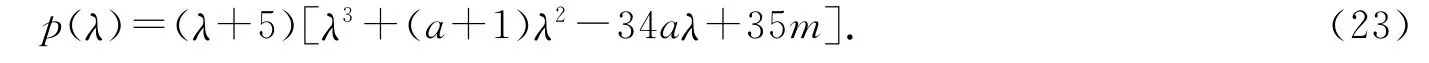
当－1＜a＜0，m＞0，－34a（a＋1）＞35m时，平衡点E0渐近稳定；当－1＜a＜0，m＞0，－34a（a＋1）＝35m时，满足Hopf分岔发生的参数条件.令a＋1＝0，－34a＝0或35，m＝0，－34a（a＋1）－35m＝0，画出a－m参数空间上平衡点的稳定域，如图11所示.其中曲线Li，i＝1，2，3，4分别代表a＋1＝0，－34a＝0或35，m＝0和－34a（a＋1）－35m＝0，在曲线L4上满足Hopf分岔发生的参数条件.区域（Ⅰ）：－1＜a＜0，m＞0，－34a（a＋1）＞35m，在区域（Ⅰ）上平衡点E0渐近稳定，其他区域平衡点E0都不稳定.结合图11，取a＝－0.5，则它与L4相交点即为 Hopf分岔点，可以求得分岔临界值m0＝0.24286.此时，系统发生Hopf分岔有一个极限环产生，如图12b所示.图12a，c和d分别为取区域（Ⅰ）、区域（Ⅲ）和区域（Ⅶ）中的点所得到的相图，与图1的理论分析相符合.

图11 系统（1）在参数平面（a，m）上的稳定域

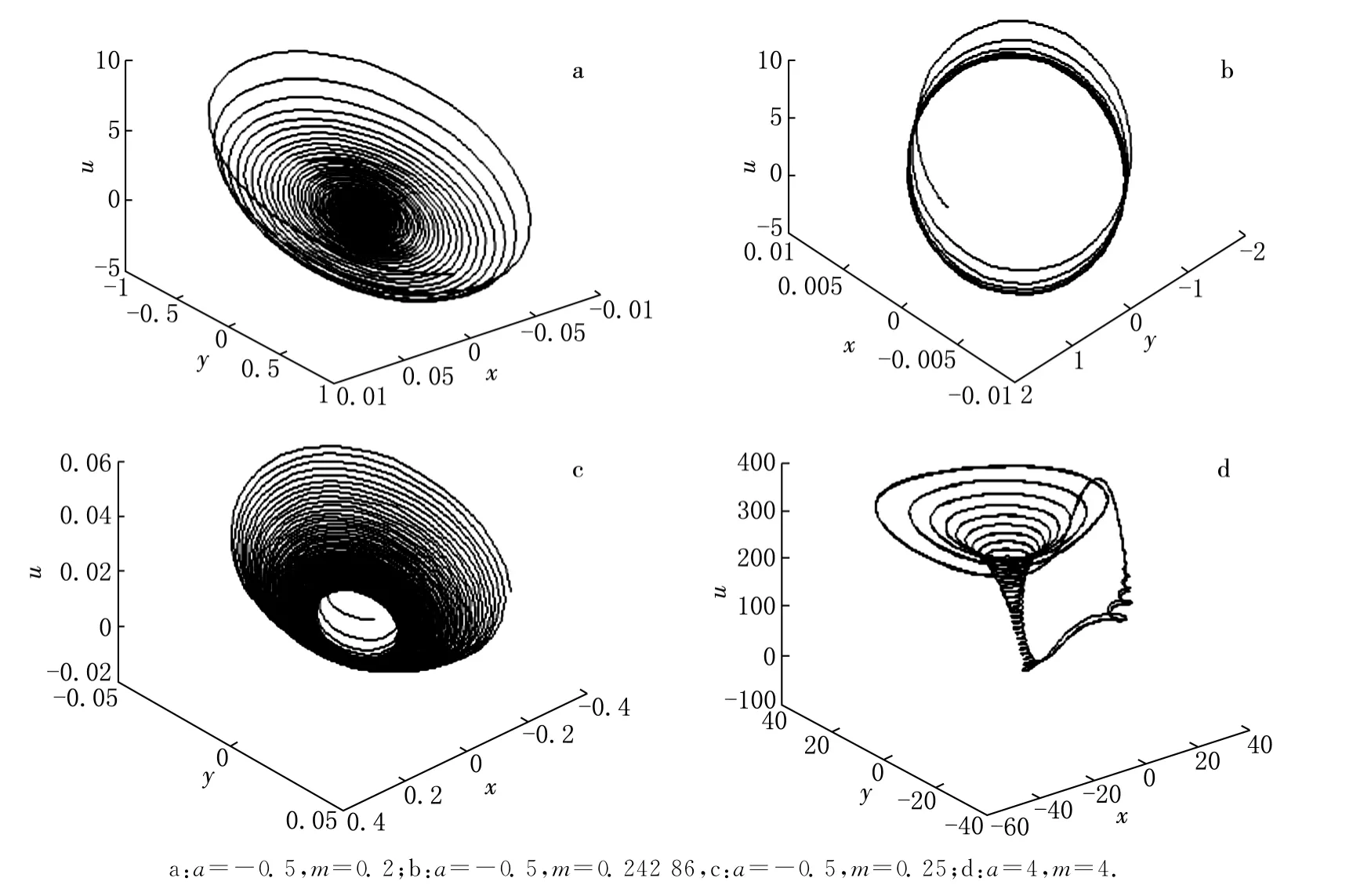
图12 系统（1）在a和m不同参数下的相图

5 结论

本文通过严格的数学推导及数值仿真研究了一个新三维混沌系统，理论分析了该系统的平衡点的稳定性，通过选取适当的分岔参数，证明了当分岔参数经过临界值时系统发生了Hopf分岔.通过计算系统的第一Lyapunov系数判断了分岔的方向和稳定性.然后进行了数值模拟，验证了理论推导的正确性.

［1］彭国俊.一个混沌系统的霍普夫分岔分析［J］.柳州师专学报，2007，22（1）：124－126.

［2］DIAS F S，MELLO L F，ZHANG J G.Nonlinear analysis in a Lorenz－like system ［J］.Nonlinear Analysis Real World Applications，2010，11：3491－3500.

［3］李群宏，徐德贵.一个类Lorenz系统的动力学分析［J］.重庆理工大学学报，2011，25（2）：112－116.

［4］李险峰，张建刚，褚衍东，等.一个新类Lorenz混沌系统的动力学分析及电路仿真［J］.动力学与控制学报，2007，5（4）：324－329.

［5］高智中，韩新风，章毛连.一个新的四维超混沌系统及其电路仿真［J］.东北师大学报：自然科学版，2012，44（1）：77－83.

［6］HASSARD，B D，KAZARINOFF，N D，WAN Y H.Theory and applications of Hopf bifurcation［M］.Cambridge：Cambridge University Press，1981：1－86.

［7］KUZNETSOV Y A.Elements of applied bifurcation theory［M］.New York：Springer，2004：293－313.

［8］ZHUANG K J.Hopf bifurcation for a new chaotic system ［J］.International Journal of Computational and Mathematical Sciences，2010，4：358－361.

［9］褚衍东，湛宁，安新磊，等.一个具有四翼混沌吸引子的新系统及其参数辨识［J］.兰州大学学报，2012，48（2）：136－140.

［10］ZHANG K M，YANG Q G.Hopf bifurcation analysis in a 4D－hyperchaotic system ［J］.J Syst Sci Complex，2010，23：748－758.

［11］薛怀庆，彭建奎，王振乾，等.超混沌Lorenz系统的电路模拟与同步［J］.兰州大学学报，2011，47（5）：117－121.

［12］SPARROW C.The lorenz equations：bifurcations，chaos and strange attractors［M］.New York：Springer Verlag，1982：26－43.

［13］SOTOMAYOR J，MELLO L F，BRAGA D C.Bifurcation analysis of the Watt governor system［J］.Computational ＆ Applied Mathematics，2007，26（1）：19－44.

［14］ZHANG J G，LI X F，CHU Y D，et al.Hopf bifurcations，Lyapunov exponents and control of chaos for a class of centrifugal flywheel governor system［J］.Chaos，Solitons and Fractals.2009，39（5）：2150－2168.