偏序群S上S-偏序系的内射包*

张 霞 ，徐彦涛

(1.华南师范大学数学科学学院，广州510631;2. Department of Mathematics，Southern Illinois University Carbondale，62901 Carbondale，USA)

设S 是一个偏序幺半群，即幺半群S 上带有一个偏序≤满足对任意的s≤t，s'≤t'，s，s'，t，t'S，都有ss'≤tt'.我们称带有映射A×S→A(元素对(a，s)映到A 中的元记为as)的偏序集(A，≤)为一个右S-偏序系，记作AS(或简写为A)，如果A 是一个S-系，并且满足对任意的a，bA，s，tS，有a≤b，s≤t⇒as≤bt.

类似地可以定义左S -偏序系. 本文只讨论右S-偏序系，因此省去“右”字. S -偏序系同态是保序并且保持S -作用的映射. 所有的S -偏序系及S-偏序系同态做成一个具体范畴，记为S-偏序系范畴.

S-偏序系(AS，≤A)的S-子偏序系B 是A 的作用封闭的子集合，即A 的子系，并且B 上的偏序为B×B∩≤A.从偏序集(A，≤A)到偏序集(B，≤B)的序嵌入是一个从A 到B 的映射h，满足a≤Aa'当且仅当h(a)≤Bh(a')，∀a，a'A. 易知，每个序嵌入都是单映射.

当S 与A 上的偏序取成离散序时，S -偏序系就是S-系. 可见，S -偏序系理论是S -系理论的推广.

设C 是一个具体范畴，由文献［1］知，称C 中的对象Q 是内射的，如果对任意的嵌入同态h:A→B，C 中的任意同态f:A→Q，存在C 中的同态g:B→Q 使得gh=f.称对象EC 是C 中对象A 的一个内射扩张如果E 是内射的，并且存在C 上的一个嵌入同态ι:A→E.

称C 中的嵌入同态η:A→B 是本质的，如果对C 中的任意同态ψ:B→C，同态的合成ψη 是嵌入同态，ψ 本身也是嵌入同态. 称对象EC 是C 中对象A 的一个本质扩张如果存在一个从A 到E 的本质同态.

对于一个偏序集P，P 的扩张E 称为是并稠密的(交稠密的)，如果E 中的每个元素都是P 中比它小的元素的上确界(下确界)［2］.

S-系的内射理论已经被广泛研究，读者可以参考文献［3］中的相关研究成果.S -偏序系内射理论的研究最早始于1986年，Skornyakov［4］研究了具有离散序的幺半群S 上的S - 偏序系，得出这样的S-偏序系是内射的必要条件，即它是一个完全偏序集. 之后，Fakhruddin［5］将这个结果推广到任意的偏序幺半群，得到:对于一个偏序幺半群S，一个内射的S-偏序系ES一定是一个完全格并且满足条件(∨{xi})s=∨{xis}，∀sS 及E 中的任意一族元素{xi}.这种S-偏序系被称为完全S -偏序系. 当S 取成偏序群时，Fakhruddin［5］得到:对于一个偏序群S，一个S-偏序系是内射的当且仅当它是一个完全S-偏序系.我们将进一步得到:对于一个偏序群S，一个S-偏序系是内射的当且仅当它是一个完全偏序集(见引理1).

关于内射包，S -系理论已有成熟的结论，即对任意的幺半群S，每个S-系都可以嵌入到一个内射包中，并且这个内射包在同构意义下唯一［6］. 对于S-偏序系理论，每个S-偏序系是否存在内射包还是一个未解决的问题. 最近的研究成果见文献［7］，该文献构造了偏序半群关于某类特殊同态(保序的submultiplicative 映射)的内射包. 而对于一般的同态，这还是一个有待解决的公开问题.

本文将讨论当S 是一个偏序群时，S -偏序系的内射包情形，得出当S 是一个偏序群时，每个S-偏序系都存在内射包，并且内射包在同构意义下唯一，最后将构造出任意一个S-偏序系的内射包. 在此基础上，进一步得出对任意的S -偏序系AS，AS的内射包既是A 的极小内射扩张，又是A 的极大本质扩张.

以下如果没有特殊说明，S 表示一个偏序群.

由文献［5］的命题7.2 知，偏序群上的偏序系是内射的充要条件是它是一个完全偏序系. 直接证明可以得到进一步的结论:

引理1 设S 是一个偏序群.则一个S-偏序系是内射的当且仅当它是一个完全偏序集.

由文献［5］的推论7.4 知每个偏序群S 上的S-偏序系都存在内射包，再由文献［1］的命题9.19，易证该内射包在同构意义下唯一. 因此，有:

推论1 设S 是一个偏序群，AS是一个S -偏序系，则AS存在唯一的内射包.

接下来将具体构造偏序群S 上任意一个S -偏序系的内射包. 由前面结论知，这个内射包在同构意义下唯一. 更进一步，我们将得到每个S-偏序系的内射包都将是它的极小的内射扩张，同时也是它的极大的本质扩张.

设A 是一个偏序集，B⊆A. 记

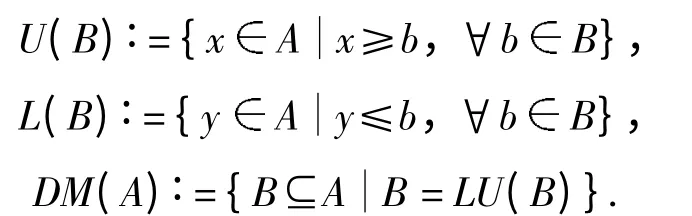
由文献［2］知，(DM(A)，⊆)是A 的Dedekind -MacNeille 完全扩张，其嵌入映射为

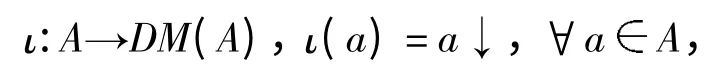
设S 是偏序群，AS是一个S -偏序系，定义一个作用我们将证明DM(A)在这个作用下关于包含关系做成一个S-偏序系.

引理2［9］设A 是一个偏序集，B1⊆B2⊆A. 则

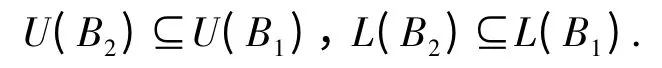
引理3 设S 是一个偏序群，AS是一个S -偏序系.则对任意的BDM(A)，sS，有

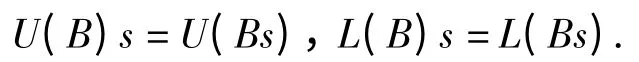
下面证明如下定理.

定理1 设S 是偏序群，AS是一个S-偏序系.则DM(A)在作用

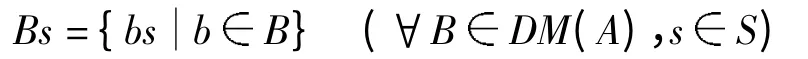
下做成一个S-系，并且关于包含关系做成一个S-偏序系.

证明 首先证明DM(A)关于定义的作用做成一个S-系.为此需要证明:对任意的BDM(A)，s，tS，都有

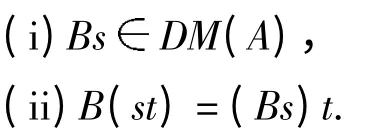
显然(ii)是成立的. 我们只需证明(i)成立，即往证，Bs=LU(Bs).

接下来需要证明DM(A)关于包含关系做成一个S-偏序系.包含关系是DM(A)上的一个偏序关系是显而易见的，因此只需要证明包含关系关于DM(A)上的系作用是相容的.

设B1，B2DM(A)，s1，s2S 满足B1⊆B2，并且s1≤s2. 易证B1s1⊆B2s1.由引理2 知

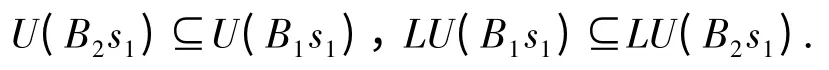
由于BisjDM(A)，i，j{1，2}，可得

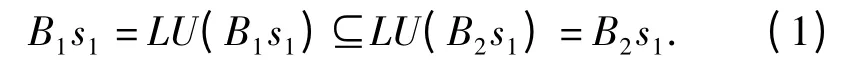
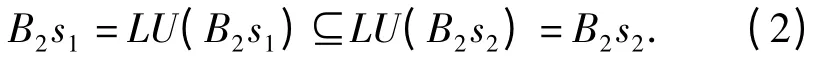
由式(1)及式(2)得B1s1⊆B2s2. 由此证明了DM(A)关于包含关系及所给的系作用做成一个S -偏序系. □

设AS是一个S-偏序系，记定理1 中DM(A)关于所定义的作用及包含关系做成的S - 偏序系为DM(A)S.接下来要构造偏序群S 上的S -偏序系AS的内射包.由推论1 知，内射包如果存在则唯一，下面将证明DM(A)S就是AS的唯一的内射包.

引理4［2］设A 是一个偏序集，E 是A 的一个扩张.则E 是A 的一个本质扩张当且仅当它既是并稠密的又是交稠密的.

定理2 设S 是一个偏序群，AS是一个S-偏序系.则DM(A)S是AS的内射及本质扩张，即DM(A)S是AS的内射包.

证明 显然，DM(A)关于包含关系做成一个完全格.由引理1 知DM(A)S是内射的.下面证明DM(A)S是AS的一个本质扩张. 定义映射

表明(as)↓⊆a↓s.故ι 是一个S-系同态.

设ψ:DM(A)S→BS是一个S -偏序系同态，满足ψι:AS→BS是序嵌入的S -偏序系同态. 下面需要证明ψ 本身也是一个序嵌入的S-偏序系同态.

由于DM(A)既是并稠密的又是交稠密的，由引理4 可得ψ 是偏序集范畴的本质扩张映射，故ψ 是一个序嵌入映射. 又由假设，ψ 是一个S -偏序系同态，最终得到ψ 也是一个序嵌入的S -偏序系同态，即DM(A)S是S-偏序系AS的本质扩张. □

最后将证明对于一个偏序群S，及任意一个S-偏序系AS，AS的内射包是它的极小的内射扩张，同时也是它的极大的本质扩张.

定理3 设S 是一个偏序群，AS是一个S -偏序系.则以下命题等价:

(1)ES是AS的内射包;

(2)ES是AS的内射且本质扩张;

(3)ES是AS的极小内射扩张;

(4)ES是AS的极大本质扩张.

证明 (1)⇔(2)由定义可得.

(2)⇒(3). 设E'S也是AS的内射扩张且E'⊆E.由E'S的内射性知，存在S-偏序系同态g:E→E'使得其中idE'是E'上的恒等同态.由于E 是A 的本质扩张，且是一个序嵌入的S-偏序系同态，可知g 也是序嵌入的S -偏序系同态.这说明E≅g(E)⊆E'，故E=E'.

(3)⇒(4). 设E'S是AS的一个本质扩张且E⊆E'. 先证明E'也是E 的本质扩张. 设f:E'S→HS是一个S-偏序系同态，满足是一个序嵌入. 则也是一个序嵌入，再由E 是A 的本质扩张知，f是一个序嵌入. 由此得E'是E 的本质扩张.

最后证明E 是A 的本质扩张.设ι:AS→DM(A)S，ι':AS→ES是自然的序嵌入. 由E 的内射性知存在S-偏序系同态g:DM(A)→E，使得gι=ι'.这说明g也是一个序嵌入，由于DM(A)也是A 的内射扩张，并且由已知E 是A 的极小的内射扩张，只有E =DM(A).又DM(A)是A 的本质扩张知，E 也是A 的本质扩张，从而是极大的本质扩张.

(4)⇒(1). 设ES是AS的极大本质扩张，DM(E)S是E 的内射包. 易证DM(E)也是A 的本质扩张.由E 的极大性知E=DM(E). 因此E 是一个完全偏序集，从而由引理1 知，E 是内射的. 继而，E 是A 的内射且本质扩张，即A 的内射包. □

［1］Adámek J，Herrlich H，Strecker G E. Abstract and concrete categories:The joy of cats［M］. New York:John Wiley and Sons，1990.

［2］Banaschewski B，Bruns G. Categorical characterization of the MacNeille completion［J］. Archiv der Mathematik，1967，18(4):369 -377.

［3］Kilp M，Knauer U，Mikhalev A. Monoids，acts and categories，with applications to wreath products and graphs［M］. Berlin，New York:Walter de Gruyter，2000.

［4］Skornyakov L A. Injectivity of all ordered left polygons over a monoid［J］. Vestnik Moskovskogo Universiteta:Seriya I，1986，3:17 -19.

［5］Fakhruddin S M. On the category of S-posets［J］. Acta Scientiarum Mathematicarum，1988，52:85 -92.

［6］Berthiaume P. The injective envelope of S-sets［J］. Canadian Mathematical Bulletin，1967，10:261 -273.

［7］Lambek J，Barr M，Kennison J F，et al. Injective hulls of partially ordered monoids［J］. Theory and Applications of Categories，2012，26:338 -348.

［8］Birkhoff G. Lattice theory［M］. 2nd ed. New York:American Mathematical Society，1948.

［9］Davey B A，Priestley H A. Introduction to lattices and order［M］. Cambridge:Cambridge University Press，1990.