强化数形结合思想 渗透参数分类整合——一道高考题引发的“绝对值函数”复习策略的思考

黄惠蓉（南安第一中学，福建 南安 362300）

强化数形结合思想 渗透参数分类整合
——一道高考题引发的“绝对值函数”复习策略的思考

黄惠蓉
（南安第一中学，福建 南安 362300）

函数作为高中数学知识体系的一条主线，在高考专题复习阶段，不仅要关注它与其余各章节知识之间的联系，而且得讲究复习策略的固化和优化，更要凸显数学思想方法的运用。以 “绝对值函数”专题复习为例，有目的地引导学生对高考试题进行探究拓展，强化数形结合思想，渗透参数分类整合可以利用有限的时间取得复习效益的最大化。

绝对值函数；复习策略；数形结合

笔者在研读全国高考考试大纲的基础上，致力于寻求“绝对值函数”这一主干知识的有效复习策略。为此，笔者对某道高考题作了两个大系列，六个小方向的拓展研究。

一、展示

（一）原题呈现2015年全国卷Ⅰ第24题（选修4-5：不等式选讲）

已知函数f（x）=|x+1|-2|x-a|，a＞0

（I）当a=1时，求不等式f（x）＞1的解集；

（II）若f（x）的图象与x轴围成的三角形面积大于6，求实数a的取值范围。

思路分析：审题是解题的第一步，也是最关键的一步。从题眼入手，理解题意、挖掘内涵，并找出各知识点之间千丝万缕的联系，然后形成初步的解题思路。分析函数解析式的结构特征，此函数含两个绝对值符号，故它是分段函数，如何对参数a进行分类讨论，进而去绝对值符号，写成分段函数是本题的难点。

（I）运用“零点分区间法”进行分类讨论去绝对值符号求解一元一次不等式，体现转化与化归思想；分类时强调自变量取值端点设置应做到“不重复不遗漏”，结论整合时遵循“内交外并”原则。

（II）数形结合，先求出的三个顶点的坐标，进而得出三角形的面积表达式，再列不等式（一元二次不等式）求解。

解析：（I）当a=1时，f（x）＞1即|x+1|-2| x-1|＞1；

当x＜-1时，不等式可化为-x-1+2x-2＞1，即x＞4与x＜-1矛盾，舍去；

当x＞1时，不等式可化为x+1-2x+2＞1，即x＜2，故1＜x＜2。

（II）因为a＞0＞-1，依题意可得，

得y=a+1；令-x+1+2a=0得x=2a+1.

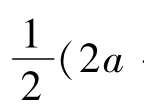
∴a+1＜-3（舍去）或a+1＞3，故a＞2

综上述，a的取值范围为（2，+∞）.

评析：学生解题所暴露出来的问题，如数形结合思想的欠缺、分类整合方法不得当等，具体体现在以下三方面：两个零点大小比较，即分类讨论标准模糊；整合结论没有遵循“内交外并”原则；构作函数图象（直线、射线）根深蒂固地认为只有两点才能确定一直线，而忽略了直线上的一点、斜率这两要素也能确定一条直线。

上述高考题结构简洁、构思精巧、原生形态、意境深远，有着良好的检测功能与较强的命题导向功能，很值得我们一同来鉴赏与探求，其分类整合思想、数形结合思想、转化与化归思想的运用更是符合新课程的理念精神，有助于学生融会贯通教材知识，利于启发学生思维、拓宽知识视野，提高分析和解决问题的能力。函数作为高中数学知识体系的一条主线，在高考专题复习阶段，不仅要关注它与其余各章节知识之间的联系，而且得讲究复习策略的固化和优化，更要凸显数学思想方法的掌握。以“绝对值函数”专题复习为例，如何利用有限的时间，取得复习效益的最大化？笔者认为：有目的地引导学生对高考试题进行探究拓展，强化数形结合思想，渗透参数分类整合是很有必要的。

（二）拓展系列1（铺垫）去除原题的约束条件，求解步骤（II）。基于“零点分区间法”，着重强调对参数的分类讨论以及结论的整合思想，当然解题过程中也不能忽视数形结合思想的运用。

思路分析：利用分类讨论思想，通过对参数的缜密讨论，去绝对值符号，再运用转化与化归思想，将绝对值不等式转化为一元一次不等式求解。但是，大家都知道分类讨论向来是学生的“软肋”，尤其是在分类界点的确定、讨论过程的完备性更应给学生提个醒。

解析：当a＜-1时，

∴a+1＜-3或a+1＞3（舍去），故a＜-4.

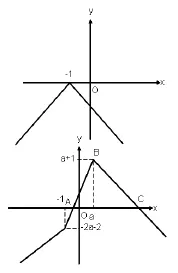
当a=-1时，函数f（x）=-|x+1|，如图f（x）仅与x轴交于一点（-1，0），不合题意，舍去。

当a＞-1时，与原题解法同，得a＞2；

综上述，a的取值范围为（-∞，-4）∪（2，+∞）。

根据试题的特征，引导学生对问题本质进行一定的探究，有节奏地拓展试题所涉及内容的深度与广度，即能达到做一题通一片的效果。［1］

拓展系列1 函数、方程、不等式可谓是“一胞三胎”，通过函数的图象可将三者紧密地结合在一起。

拓展系列1.1数与形式数学研究的两个重要方面，抽象的数学概念和严谨的数量关系可借助于图形的形象化、直观化，揭露其深层本质。

已知函数f（x）=|x+1|-2|x-a|，若不等式f（x）＞1有解，求实数的取值范围。

思路分析：本拓展例题旨在，在“数”中构“形”，即根据代数问题具有的几何特征，进而判断不等式有解的情况。具体步骤是分别画出“形”——函数f（x）图象与直线y=1。不等式f（x）＞1有解，实则函数f（x）部分图象应在直线y=1上方，进而转化成fmax（x）＞1。

解析：依题意，只需fmax（x）＞1即可。

当a＜-1时，fmax（x）=-a-1＞1，得a＜-2；

当a=-1时，fmax（x）=0＞1矛盾，舍去；

当a＞-1时，fmax（x）=a+1＞1，得a＞0。

综上述，a的取值范围为（-∞，-2）∪（2，+∞）。

评析：该题条件以绝对值不等式有解的形式给出，求参数的取值范围。入口较宽，可以从多角度进行思考。题目精致小巧，能较好地考查学生的数学思维水平。

二次拓展，请进一步求出不等式f（x）＞1的解集。

解析：当a＜-2时，令x-1-2a=1得x=2a+ 2；

评析：几何直观能启迪思路，帮助我们更具体生动地理解数学知识，善于借助几何直观学习和理解知识，是数学学习中的重要方法。

拓展系列1.2本拓展例题旨在，从“数”中构“形”，解决含参数方程根的个数情况。

已知函数f（x）=|x+1|-2|x-a|，若关于x的方程f（x）=a2+2a-5有且只有一个实数根，求实数a的值。

思路分析：本题考查要求层次有所提升。这是一个关于x的方程实根的个数问题，虽然方程中含有参数a，但仍可将其视作一个相对固定的常数，延续上题的解题思路，转化为函数f（x）图象与直线y=a2+2a-5的交点问题。由此，我们只是稍作“变换”与“变形”，还原其问题本质，使得看似陌生的问题转化为熟悉的题型。

解析：当a＜-1时，-a-1=a2+2a-5，得a =-4或a=1（舍去）；

当a=-1时，0=-6矛盾，舍去；

当a＞-1时，a+1=a2+2a-5，得a=-3（舍去）或a=2。

综上述，a=-4或a=2。

二次拓展，若关于x的方程f（x）=a2+2a-5有两个不相等实数根，求实数的取值范围。

解析：当a＜-1时，-a-1＞a2+2a-5，得-4＜a＜1，故-4＜a＜-1；

当a=-1时，0＞-6，满足题意；

当a＞-1时，a+1＞a2+2a-5，得-3＜a＜

2，故-1＜a＜2。

综上述，a的取值范围为（-4，2）。

拓展系列1.3 A是B的充分条件，表示A成立可以推出B成立，全国卷中常出现用证明A成立的方法去证B成立，本拓展例题即运用充分性的方法，证明多参数的不等式恒成立问题。

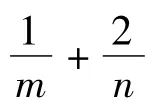
当a＜-1时，fmax（x）=-a-1≤8，得-9≤a ＜-1；

当a=-1时，满足题意；

当a＞-1时，fmax（x）=a+1≤8，得-1＜a≤7。

综上述，a的取值范围为［-9，7］。

（三）拓展系列2 关注形同而质别的“不等式恒成立”与“解的存在性”问题。［2]

拓展系列2.1通过引入参数，求解有关不等式“恒成立”问题，结合使用绝对值不等式的几何意义。求参数范围问题，本质上就是构建函数求函数的值域问题。

已知函数f（x）=|x+1|-2|x-1|，若对任意实数s，总有f（s）≤t-f（-s）恒成立，求实数t的取值范围。

解析：由f（s）≤t-f（-s），得|s+1|-2|s-1 |+|-s+1|-2|-s-1|≤t即-（|s+1|+|s-1 |）≤t对任意s∈R恒成立，故问题转化为求［-（|s+ 1|+|s-1|）］max≤t；

而由绝对值不等式的几何意义，可得|s+1|+|s -1|≥2，故t≥-2；

综上述，t的取值范围为［-2，+∞）。

拓展系列2.2 作符号上的细微调节及部分措辞改变，可将不等式转化为“存在性”问题，过程当中既可以运用数形结合思想解题，也用了绝对值不等式的几何意义。

已知函数f（x）=|x+1|-2|x-1|，若存在实数s，使得f（s）≤t+f（-s）成立，求实数t的取值范围。

解析：由f（s）≤t+f（-s），得|s+1|-2|s-1 |-|-s+1|+2|-s-1|≤t；

即存在实数s，使得3（|s+1|+|s-1|）≤t成立；

此时，问题转化为求［3（|s+1|+|s-1|）］min≤ t；

而由绝对值不等式的几何意义，可得|s+1|+|s -1|≥2，故t≥6；

综上述，t的取值范围为［6，+∞）。

评析：解题之后，要引导学生做好解题反思，帮助他们反思思维过程，找到解题盲点（易错点、易混点、易忘点），突破解题障碍（思维的障碍、计算的障碍、转化的障碍），形成较优的解题思路和方法。此外，还要做适当变式，拓展学生思维。

二、结束语

在探索专题复习策略的教学实践中，笔者认为还应注意以下两方面问题。

1.在解题教学中应加强指导学生从宏观上发现、挖掘解题线索。因为专题复习题大多遵循多个知识点处交汇命题原则，而这些知识点多分布于教材的不同模块之中。故应先辨别题目归属哪一大类型题，如若是函数问题，则应经进一步引导学生分析归纳出研究函数问题的基本策略：首先，题中涉及的函数是指、对数函数，还是三角函数等基本初等函数或是多种函数的复合；其次，是否可以在“数”中构“形”，运用数形结合思想，有函数图象的变换手段来研究其性质；再者，虽然函数给出了具体解析式，但在作图上有困难，是否可借用“导数”这一有力工具研究其单调性、极值、最值等性质。

2.在加强对学生进行解题指导的同时，还应教给学生反思的方法，促进学生元认知能力的提升，即引导学生在解题后对解题策略的总结。引导学生对题目考查的知识点与数学能力进行反思等，并且让学生认识到只要基本概念掌握扎实，数学思想方法运用得当，运算能力有力支持，再复杂的问题都可以攻克。

［1]袁守义.题不在多，反思则行［J].数学通讯，2014（1）.

［2]黄惠蓉.互动探究活动，促进知识的意义建构［J].福建中学数学，2012（10）.

G633

A

1673-9884（2015）09-0115-04

2015-08-05

黄惠蓉（1976-），女，福建南安人，南安第一中学高级教师。