MOMENTS OF PASSAGE TIMES AND ASYMPTOTIC BEHAVIOR OF INCREASING SELF-SIMILAR MARKOV PROCESSES∗

(胡巍)(刘禄勤)

1.Department of Mathematics,Jiangsu University of Technology,Changzhou 213001,China

2.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China

E-mail:huw721@whu.edu.cn;lqliu@whu.edu.cn

MOMENTS OF PASSAGE TIMES AND ASYMPTOTIC BEHAVIOR OF INCREASING SELF-SIMILAR MARKOV PROCESSES∗

Wei HU(胡巍)1,2Luqin LIU(刘禄勤)2

1.Department of Mathematics,Jiangsu University of Technology,Changzhou 213001,China

2.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China

E-mail:huw721@whu.edu.cn;lqliu@whu.edu.cn

By using Lamperti’s bijection between self-similar Markov processes and L´evy processes,we prove fniteness of moments and asymptotic behavior of passage times for increasing self-similar Markov processes valued in(0,∞).We also investigate the behavior of the process when it crosses a level.A limit theorem concerning the distribution of the process immediately before it crosses some level is proved.Some useful examples are given.

self-similar process;Markov process;L´evy process;subordinator;passage time; moment

2010 MR Subject Classifcation60G18;60J25

1 Introduction

In recent years there has been a growing interest in the theory of positive self-similar Markov processes.Recall that a Markov process X=(Ω,F,Ft,Xt,θt,Px)with state space(0,∞)is called self-similar Markov process of index α＞0 if its transition function P(t,x,A)satisfes

Clearly,(1.1)is equivalent to say that for any x＞0,b＞0

Lamperti in his celebrated paper[1]proved that for each fxed α＞0,there is a bijective correspondence between self-similar Markov processes of index α and real-valued L´evy processes. It was shown by[1]that every self-similar Markov process with state space(0,∞)automatically is strongly Markovian and has“nice path”,so it is a Hunt process in the sense of[2].Some weak convergence results and explicit identities associated with self-similar Markov processes valued in(0,∞)were obtained in[3]and[4],respectively.Recently,[5]studied the fuctuation theory and exit systems for positive self-similar Markov processes.For increasing self-similar Markov processes,[6]specifed their asymptotic behavior in law as the starting point x→0+and[7]determined their behavior at infnity by a law of iterated logarithm.[8]studied the hitting probability and polarity for a class of self-similar Markov processes.

Study on distributions and moments of frst hitting and last exit times for Markov processes is attracting more and more attention.The stability of passage times for L´evy processes were discussed in[9].The moments of last exit times for transient semi-stable processes were investigated in[10].In[11]it was proved that the distributions of frst passage times for three special class of L´evy processes including symmetric stable processes and stable subordinators are power laws.[12]considered the fniteness of the frst passage times when the L´evy processes cross a curved boundary.[13]studied the asymptotics of the frst-passage time of a one-dimensional difusion process through a stochastic boundary.We refer to[14,15]and[7]for more results about passage times and limit theorems for L´evy processes and positive self-similar Markov processes.

In this paper we investigated the moments of frst passage times of increasing self-similar Markov processes valued in(0,∞).We give some conditions for the fniteness of moments of frst passage times when the self-similar Markov processes cross above horizontal,linear or certain curved boundaries.We also get some asymptotic behavior about the frst passage when the increasing self-similar Markov processes cross a horizontal line.Section 2 introduces the associated L´evy process and provides some lemmas;In Section 3,the fniteness of moments and asymptotic behavior of passage times were proved;a limit theorem concerning the distribution of the process immediately before it crosses some level is obtained.In Section 4,some illustrating examples are given.

We will use the notations and terminology adopted in[2]except explicitly stated otherwise.

2 Preliminaries

Suppose that X=(Ω,F,Ft,Xt,θt,Px)be a self-similar Markov process of index α＞0 with state space(0,∞)whose sample paths are non-decresing on[0,∞).Let us introduce the additive functional

which is continuous and strictly increasing for t∈[0,∞),and satisfes φ∞:=limt→∞φt=∞a.s.(see[1]for details).Let τt=τ(t)be the inverse function of φt,i.e.,

We now defne a new process as follows:

It is well known from[1]that

The law of{Yt,t≥0}is uniquely determined by its Laplace transform

where ψ(λ),the Laplace exponent of{Yt,t≥0},is given by

with the drift coefcient δ and L´evy measure Π.It follows from(2.3)and(2.4)that

It is known from[16],Chapter 4 that

where eA:={ex:x∈A}.

It follows from(2.1)and(2.5)that

Letting t→∞in(2.2)and using self-similarity(2.5),one can see that

That is,{Xt,t≥0}is transient.

For r＞0,we defne the frst passage time of{Xt,t≥0}over the level r by

with the usual convention inf∅:=∞.Accordingly,the frst passage time for{Yt,t≥0}is defned by

Since the paths of{Xt,t≥0}are non-decreasing,one can see that for any r≥x＞0

That is,the frst and last passage times of{Xt,t≥0}across level r are both equal to the sojourn time in interval[x,r].

ProofBy the defnition,we have

ProofIt follows from Lemma 2.1 that The second equality follows from this and the defnition of left limit.

Lemma 2.3For any r≥x＞0,we have

where x-1A:={x-1y:y∈A}.

ProofIt follows from(2.6)and Lemma 2.1 that

Finally,(2.9)can be proved similarly.

Lemma 2.4For any β＞0,r≥0,we have

ProofAccording to Lemma 2.1 and the defnition of Ter,we have

On the other hand,Noting that{Xt,t≥0}has increasing paths,we get

Thus(2.10)is proved.

3 Main Results

It is clear that

The following theorem says that except this degenerate case the passage times have fnite moments of any order.To prove our result,we defne

which is a kind of truncated mean;when E1(Y1)＜∞,then A(x)→E1(Y1)as x→∞.

Theorem 3.1Assume that δ＞0 or Π/=0.Then

ProofFor any fxed r≥x＞0,β＞0,by Lemma 2.3 and Lemma 2.4,we have

In[12],the author considered the fniteness of frst passage when the L´evy processes X cross the curved boundary.The next theorem is an analogous results for self-similar processes X.For any r＞0,a＞0,we defne

Let f(t)be a positive nondecreasing function on(0,∞),which is regularly varying with index ρ as t→∞(we write this as f(t)∈RVρ).

Theorem 3.2Assume that δ＞0 or Π/=0.Let g(t)be a nondecreasing positive function on[u,∞).

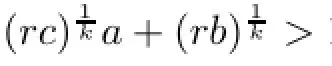
Proof(1)Since X has increasing paths,we have

so we can get that

From the right hand of(3.2),we have that

(2)Note that t≤τt.We have

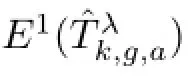
From this we can get our conclusion. ?

Remark 3.3Taking g(t)≡1 with c=1 and b=0,we can get Theorem 3.1 in the case of x=1.

The next theorem deals with the asymptotic behaviors of{Xt,t≥0}and its passage times for small and large times.

Theorem 3.7Let the notations be specifed as before,and x＞0.

(1)One has

(2)If Π((0,1))=∞,then

If Π/=0,then

Proof(1)Note that

Since{Yt,t≥0}is of bounded variation with drift δ≥0,by Theorem 2.2.(a)(ii)of[9],one has

This enables us to get

Theorem 3 of[18]says that,in present case,

Thus(3.4)follows.Noting that

by Theorem 4 of[18]and self-similarity(2.5),one gets(3.5)immediately.?

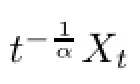
Theorem 3.8For any x＞0,the following assertions are equivalent:

(3)The Laplace exponent ψ(λ)is regularly varying at 0(respectively,at∞)with index η∈[0,1].

In this case,the limit distribution in 1.is independent of x and specifed by the following. For η=0(respectively,η=1),it is the Dirac point mass at 0(respectively,at 1).For η∈(0,1), it is the generalized arcsine law with parameter η,that is the measure on[0,1]given by

ProofSince r→x+⇔logrx-1→0+,by Theorem 6 of[14]p.81,it is enough to prove that for any y∈R,r＞x

But these are simple consequences of self-similarity(2.5)and the fact that YˆTlogr-=logXTr-, which comes from Lemma 2.2.?

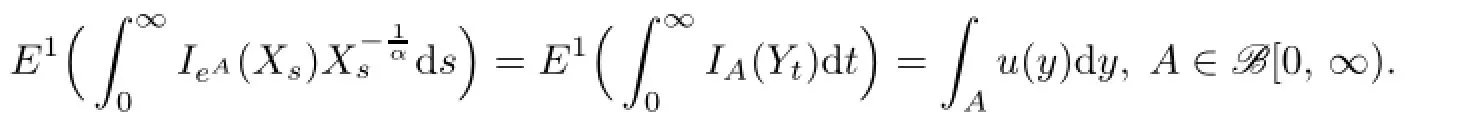
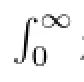
Theorem 3.10Let r＞x＞0.If δ=0,then Px(XTr＞r)=1;If δ＞0,then Px(XTr=r)=δu(logr-logx).

ProofIt follows from(2.8)that Px(XTr＞r)=P1(XT(rx-1)＞rx-1).So we only need to consider the case x=1.

Let δ=0 frstly.Theorem 4 of[14]p.77 says that P1(YˆTv＞v)=1 for every v＞0.On the other hand,it follows from Lemma 2.2 that

Therefore,P1(XTr＞r)=P1(YˆTlogr＞logr)=1 for any r＞1.

Now assume δ＞0.It follows from Theorem 5 of[14]p.79 that

On the other hand,it is easy to see from(3.6)that

This together with(3.7)gives the desired result.?

4 Examples

Example 4.1Let X=(Ω,F,Ft,Xt,θt,Px)be the Hunt process with state space(0,∞) having transition function

where constants α＞0,c＞0.It is easy to verify that X is a self-similar Markov process with index α.Let Y={Yt,t≥0}be the L´evy process defned by(2.1).

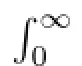
For any ε∈(0,1),

It follows from Theorem 3.8 that

Example 4.2Let X be associated to Y as above,and let γ∈(0,1).Assume that Y is γ-stable subordinator with L´evy measure

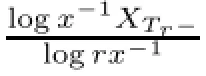
According to Theorem 3.10,Px(XTr＞r)=1,r＞x.Let r＞1.Since P1(XTr＞r)=1 and XTr-≤r,we fnd that P1(XTr≤y)=0 if y≤r and P1(XTr-＞r)=0.It follows from Theorem 3.7 that

For any 0＜ε＜1-γ,

For any 1-γ≤ε＜1,

Example 4.3Suppose that X=(Ω,F,Ft,Xt,θt,Px)is a self-similar Markov process with underlying L´evy process Y={Yt,t≥0}which is a gamma process,i.e.,Y is a subordinator with L´evy measure

Since the drift coefcient δ=0,by Theorem 3.10,we obtain Px(XTr＞r)=1 for r＞x＞0. Note that ψ(λ)is regular varying with index 1 at 0 and 0 at∞.From Theorem 3.7,we get

For any ε∈(0,1),

From Theorem 3.8,we get

[1]Lamperti J.Semi-stable Markov processes.Z Wahrscheinlichkeitstheorie Verw Gebiete,1972,22:205-225

[2]Blumenthal R M,Getoor R K.Markov Processes and Potental Theory.New York:Academy Press,1968

[3]Caballero M E,Chaumont L.Weak convergence of positive self-similar Markov processes and overshoots of Levy processes.Ann Probab,2006,34:1012-1034

[4]Chaumont L,Kyprianou A E,Pardo J C.Some explicit identities associated with positive self-similar Markov processes.Stoch Proc Appl,2009,119:980-1000

[5]Chaumont L,Kyprianou A,Pardo J C,Rivero V.Fluctuation theory and exit systems for positive selfsimilar Markov processes.Ann Probab,2012,40:245-279

[6]Bertoin J,Caballero M.Entrance from 0+increasing semi-stable Markov processes.Bernoulli,2002,82: 195-205

[7]Rivero V.A law of iterated logarithm for increasing self-similar Markov processes.Stochastics and Stochastic Reports,2003,75:443-472

[8]Xiong S,Liu L.On the hitting probability and polarity for a class of self-similer Markov presses.Acta Math Sci,1999,19(2):226-233

[9]Grifn P S,Maller R A.Stability of the exit time for Levy processes.Adv Appl Probab,2011,43:712-734

[10]Sato K,Watanabe T.Last exit times for transient semistable processes.Ann I H Poincare,2005,41: 929-951

[11]Koren T,Klafter J.First passage times of Levy fights coexisting with subdifusion.Physical Review E, 2007,76:031129 1-5

[12]Doney R A,Maller R A.Moments of passage times for Levy processes.Ann I H Poincare,2004,40:279-297

[13]Abundo M.On the frst-passage time of a difusion process over a one-side stochastic boundary.Stoch Anal Appl,2003,21(1):1-23

[14]Bertoin J.Levy Processes.Cambridge:Cambridge University Press,1996

[15]Bertoin J,Yor M.Exponential functionals of Levy processes.Probability Surveys,2005,2:191-212

[16]Gikhman I I,Skorokhod A V.The Theory of Stochastic Processses II.Berlin:Springer-Verlag,2004

[17]Bertoin J.Subordinators:Example and Applications.Berlin:Springer-Verlag,1999

[18]Erickson K B,Maller R A.Finiteness of integrals of functions of Levy processes.Proceedings London Mathematical Society,2004,94(2):386-420

[19]Bertoin J,Yor M.The entrance laws of self-similar Markov processes and exponential functionals of Levy processes.Potential Analysis,2002,17:389-400

∗Received July 10,2014;revised April 26,2015.Research supported in part by the National Natural Science Foundation of China(11171262,11171263).