带有势约束的组合最优化的一种解法
曲铁平,里 莉
(1.沈阳理工大学 理学院,辽宁 沈阳 110159;2.沈阳化工大学 数理系,辽宁 沈阳 110114)
带有势约束的组合最优化的一种解法
曲铁平1,里 莉2
(1.沈阳理工大学 理学院,辽宁 沈阳 110159;2.沈阳化工大学 数理系,辽宁 沈阳 110114)
从经典的马克维茨投资组合问题引出一个一般的组合最优化模型,并给出此模型的一个解法.首先,由拉格朗日分解从原模型的对偶问题得出一个二阶锥规化的松弛.其次,给出一个新的含混合整数二次约束的二次规化的改进.最后,证明了此改进的连续松弛问题比原问题的连续松弛问题更紧.
拉格朗日分解;二阶锥规化;组合最优化
组合最优化的应用十分广泛,但因为它是一个NP难问题,使得求得最优解的过程变得异常困难,即不可能在多项式时间内寻得其最优解.先以投资组合的经典问题为例看一下组合最优化的求解模型.马克维茨投资组合模型[1-2]在投资组合理论中十分重要,他的期望—方差模型中用期望度量投资的期望收益,用方差度量组合风险.已有很多关于带有势约束和二次约束的组合最优化模型的求解成果,比如Bertsimas等[3]提出了一种分支定界法,其中子问题的连续松弛是用Lemke方法求解.Bonami等[4]研究了带有整数约束和最小买入约束的投资组合问题,其中也用了分支定界方法.Shaw等[5]提出了一种建立在拉格朗日松弛基础上的分支定界法求解带有势约束的期望—方差模型,在分支定界步骤中的每个子问题的拉格朗日对偶是用次梯度的方法求解.不过以上方法在解决此类组合优化问题时只能得到近似解,且近似程度也不一定很好.本文针对带有势约束和二次约束的二次规化问题提出一种近似解法,且可证明此近似解的紧性较好.这不仅为此类组合最优化问题提供了一个更好的下界,具有一定的理论意义,而且为投资组合等领域的问题提供了更好的近似解,也具有一定的应用意义.
1 一般模型
关于投资组合问题的经典的期望—方差模型是考虑市场有n个可投资资产,令R1表示第i个资产的随机收益,x=(x1,x2,…xn)T是各个资产的投资权重,所以投资组合的总收益的期望和方差分别为r(x)=μTx,σ(x)=xTΣx,其中μ=(μ1,…,μn)T,而μi=E(Ri),协方差矩阵Σ=(σij),而σij=E[(Ri-μi)(Rj-μj)],所以马克维茨经典的期望—方差模型如下:
minxTΣx
s.t.μTx≥ρ
x∈X
(1)
式中,ρ表示总收益水平的常数;X是由预算等其他市场约束确定的集合.
考虑到现实中的约束情况,在上述经典模型中加入用于限制投资资产数量的势约束和最小买入约束,即
|S(x)|≤K,xi≥ai,∀i∈S(x),其中投资资产集合S(x)={i|xi≠0},0 更为一般的投资组合模型为 (2) 式中:Qi∈Sn(i=1,2)是半正定矩阵;Di是非负对角矩阵;ci∈Rn(i=1,2);A∈Rm×n;b∈Rm;u∈Rn是给出x的上界. 讨论如何使用拉格朗日松弛技术得到问题(2)的一个凸紧松弛.由拉格朗日分解从模型(2)的对偶问题得出一个二阶锥规划松弛,给出一个新的混合整数二次约束的二次规划改进,此改进的连续松弛恰好等价于二阶锥规划松弛. 2.1 拉格朗日分解 通过引入一个0-1变量yi∈{0,1}将问题(2)等价成一个混合整数二次约束的二次规划问题: (3) 如果将约束中的0-1集合{0,1}n改为[0,1]n,问题(3)即松弛为一个二次约束的二次规划问题.先引入变量z=x,上述问题(3)等价于: (4) d1(λ,γ)=minxT(Q1+λQ2)x+(c1+λc2-γ)Tx s.t.Ax≤b0≤x≤u (5) d2(λ,γ)=minzT(D1+λD2)z+γTz s.t.eTy≤K aiyi≤zi≤uiyi,i=1,2,…,n y∈{0,1}n (6) 此问题的对偶问题为 maxd(λ,γ) s.t.λ≥0,γ∈Rn (7) 根据弱对偶性,总有v7≤v3=v2,其中v1表示规划问题i的最优解,i=2,3,7. 2.2 二阶锥规划松弛 将对偶问题(7)松弛为一个二阶锥规划问题,根据强对偶定理和锥对偶性,可将问题(7)松弛为下面的半正定规化问题: (8) 式中X∈Sn为对称矩阵.由锥对偶定理[6],如果问题(8)是严格可行的,那么强对偶性成立,即没有对偶间隙,假设在问题(3)的可行域中存在相对内点,那么由此假设可知问题(8)的可行域也是严格可行的. 注意到Qi∈Sn(i=1,2)是半正定矩阵,可以用xTQ1x和xTQ2x分别代替X·Q1和X·Q2,那么问题(8)变为下列问题: (9) 定理1说明问题(9)比问题(3)的松弛问题(4)更紧. 定理1v4≤v9≤v2,其中vi表示规划问题(i)的最优解,i=2,4,9. 2.3 混合整数二次约束的二次规划改进 已知二阶锥规化问题(9)是下面的问题(10)的连续松弛: (10) 定理2指出问题(10)与问题(3)等价. 定理2 (x,y,δ)是问题(10)的解当且仅当(x,y)是问题(3)的解,进而有v10=v3,其中v1表示规划问题(i)的最优解,i=3,10. 从定理1与定理2看到问题(10)是比标准的问题(3)更为有效的改进,因为问题(10)的松弛问题(9)比问题(3)的松弛问题(4)更紧. 本文对一类带有势约束和二次约束的组合最优化模型求解提供了一个更好的下界,提高了解的近似程度,具有一定的理论意义,而且为投资组合等领域的问题提供了更好的近似解,也具有一定的应用意义. [1]Markowitz HM.Portfolio selection[J].Finance,1952,(7):77-91. [2]Markowitz H.M.Portfolio selection:Efficient Diversification of Investments[M].Wiley,NewYork,1959. [3]Bertsimas D,Shioda R.Algorithm for cardinality-constrained quadratic optimization[J].Comput.Optim.Appl,2009,(43):1-22. [4]Bonami P,Lejeune M.A.An exact solution approach for portfolio optimization problems understochastic and integer constraints[J].Oper.Res,2009,(57):650-670. [5]Shaw D,Liu S,Kopman L.Lagrangian relaxation proceduer for cardinality-constrainedportfolioo ptimization[J].Optim.Methods Softw,2008,(23):411-420. [6]Vandenberghe L,Boyd S.Semidefinite programming[J].SIAM Rev,1996,(38):49-95. (责任编辑:马金发) A Method of Solving Combination Optimization with Cardinality-constrained QU Tieping1,LI Li2 (1.Shenyang Ligong University,Shenyang 110159,China;2.Shenyang Huagong University,Shenyang 110114,China) A method for solving a general combination optimization model is introduced from the classical Markowitz portfolio selection problem.The first,a second-order cone program’s relaxation is obtained from the dual of original model via Lagrangian decomposition.The next,a new mixed integer quadratically constrained quadratic program reformulation presented.The last,it is shown that the reformulation’s continuous relaxation is tighter than the original program’s. Lagrangian decomposition;second-order cone program;combination optimization 2014-07-07 曲铁平(1960—),男,副教授,研究方向:基础数学。 1003-1251(2015)03-0067-03 O221.7 A
2 拉格朗日分解和混合整数二次约束的二次规划改进







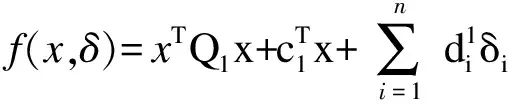


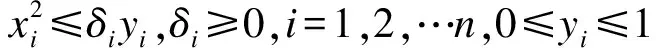

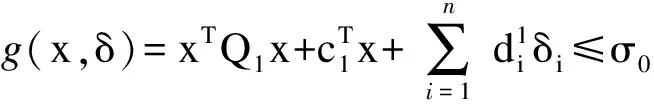
3 结束语

