Markov链中的转移过程张量与超随机张量

朱桂满，赵金玲，徐 尔，汤国斌

（北京科技大学 数理学院，北京100083）

0 引 言

2005年，Qi Liqun［1］首次提出了张量特征值与张量特征向量的概念，引起了广泛的关注．人们相继提出了许多张量的相关概念和性质，其中对于特殊张量的研究也十分活跃．Qi Liqun［1］给出了高阶张量对称的定义，研究了超对称张量的性质，并 定 义 了 张 量 的 秩［2］．2011 年，Chang 又补充了弱对称张量［3］和本原张量［4］的定义．同年，Yang Qingzhi等定义了随机张量［5］并给出了相关性质．考虑到随机矩阵是随机数学中研究Markov链的有力工具，但在Markov链的研究中，n 步转移概率矩阵中存储的信息仅表示状态i 经n 步到达状态j 的总概率，而不能从中直接读出途中经过各状态的概率．本文提出通过张量来存储n 步转移过程中各种可能情况的概率．依托于Markov链，类似于双随机矩阵的结构提出了超随机张量，并讨论了此类特殊张量的一些性质．

所谓张量，即是高维数组．例如，向量可以看成一阶张量，矩阵可以看成二阶张量．

设A＝（ai1…im），其中ai1…im∈R（ij＝1，…，n；j＝1，…，m），则A 称为m 阶n维实张量，记为A∈R［m，n］，A 中有nm个元素，若ai1…im≥0，则称A 为非负张量［6］．设x＝（x1，…，xn）为n维向量，记x［m－1］＝（xm－11，…，xm－1n）T．若存在（λ，x）∈C×（Cn＼｛0｝），使得

其中

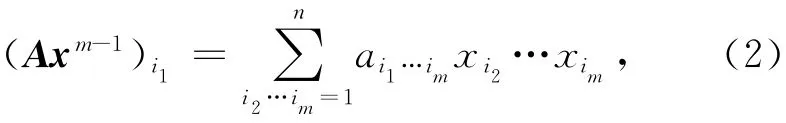
则称λ为张量A 的特征值，x为特征值λ 对应的特征向量［6］．若λ与x 分别为实数和实向量，则称λ为张量A 的H－ 特征值，否则称λ为A 的N－ 特征值．张量A的谱半径为ρ（A）＝max｛｜λ｜∶λ为A 的特征值｝［7］．张量A 被称为超对称［1］的，当且仅当ai1…im＝aδ（i1…im）对所有的σ∈δm成立，这里δm为m 个指标的任意排序所组成的集合．

引理1［8］（Chapman－Kolmogorov 方 程） 设

Markov链的状态空间为E，i，j，k∈E，不作齐次性假定，那么当时刻r＜s＜t时，有pij（r，t）＝∑k∈Epik（r，s）pkj（s，t）．对齐次性马氏链，上述方程具有更简明的形式，

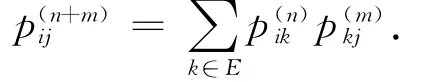
该引理中的两个等式即为求Markov链多步转移概率的Chapman－Kolmogorov 方程．其中pij（s，t）＝P（X（t）＝j｜X（s）＝i），表示已知s时刻处于状态i，t时刻将到达状态j的转移概率，而则表示齐次马氏链已知时刻k处于状态i，经n步转移后到达状态j 的n 步转移概率．

定义1［1］设m 为δi1…im的 下 标 指 数，当i1，…，im＝1，…，n时，

称为一个m 阶n 维的单位张量，记为I．为了简化计算，定义det（I）＝1．

1 Markov链中的随机张量与超随机张量

1．1 Markov链中的转移过程张量

对Markov链，设状态集为E，时刻r＜s＜t，对于i，j，k ∈E，记pikj（r，s，t）＝P（X（t）＝j，X（s）＝k｜X（r）＝i），表示已知r时刻处于状态i，途中s时刻经状态k，最终t时刻到达状态j 的概率．若为齐次马氏链，则转移概率与绝对时间无关．记p（n＋m）ikj＝P（X（l＋n＋m）＝j，X（l＋n）＝k｜X（l）＝i），表示已知当前处于状态i，n个时间单位后到达状态k，n＋m 个时间单位后转移到状态j的概率．称这里的pikj（r，s，t）和p（n＋m）ikj为转移过程概率．

由Markov过程的基本理论，易知转移过程概率满足如下结论：

定理1 设Markov链的状态空间为E，i，j，k∈E，不作齐次性假定，那么当时刻r ＜s＜t时，转 移 过 程 概 率 满 足pikj（r，s，t）＝pik（r，s）pkj（s，t）．对齐次马氏链，则有p（n＋m）ikj＝p（n）ikp（m）kj．

为简便计算，下面考察齐次马氏链．设其状态集 为E ＝｛1，2，…，n｝，一 步 转 移 概 率pij＝P（X（l＋1）＝j｜（l）＝i），则从状态i1依次经过i2，…，im－1到达状态（共m－1步）的概率ai1i2…im＝pi1i2·pi2i3…pim－1im，可视为转移过程概率．以这样的ai1i2…im（i1，…，im∈E）为元素，即构成一个m阶n维正方张量A ＝（ai1…im），称为转移过程张量．

1．2 超随机张量的定义

随机张量作为一种特殊张量，定义如下：

定义2［5］设A为一m 阶n维非负张量，若满足则称A 为m 阶n

维随机张量．

例1 设齐次马氏链状态集有限，如E＝｛1，2，3｝．若以P＝（pij），｛i，j∈（1，2，3）｝表示一步转移概率矩阵，三阶张量（1，2，3）｝表示两步转移过程概率．这里，ai1i2i3＝

情况1 假设

易验证，当i1＝1，2，3 时，当i2＝1 时，当i2＝2 时，；当i2＝3 时，

情况2 假设

易验证，当i1＝1，2，3 时，当i2＝1，2，3 时，当i3＝1，2，3 时，

在这两种情况下，A 均为随机张量，但情况2中的随机张量显然更为特殊．由此，引入超随机张量的定义．

定理2 设齐次Markov链的状态集E ＝｛1，2，…，n｝，假设其一步转移概率矩阵为n×n 双随机矩阵，即行和、列和均为1，则m－1步转移过程张量为m 阶n 维超随机张量．

证明：（数学归纳法）

作为领袖的蒋介石对于国民党意识形态建设的影响是党内其他人无法代替的，由此领袖的个性与局限亦会渗透于意识形态的表述之中。时势与人物是相互塑造的，蒋介石对国民党意识形态建构既受制于其本身的局限性，也无法突破外在困境。

即要证，

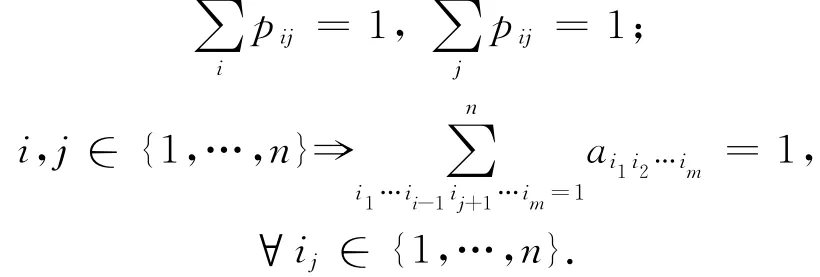
首先，设齐次Markov链的状态集E ＝｛1，2，3｝，假设其一步转移概率矩阵为3×3 双随机矩阵，P ＝（pij），｛i，j∈（1，2，3）｝，即其行和、列和均为1，这里pij指状态i经一步到达状态j 的概率．下证2 步 转 移 过 程 张 量，即3 阶3 维 张 量A ＝

（ai1i2i3），ai1i2i3＝pi1i2·pi2i3，｛i1，i2，i3∈（1，2，3）｝

是超随机张量，这里ai1i2i3指状态i1经i2到达i3的概率．

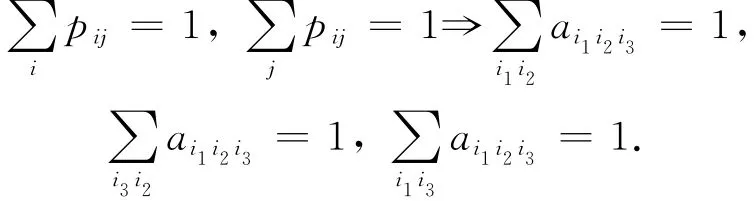
第一步：固定i1指标，令i1＝1（当i1＝2，i1＝3时同理）．

根据Chapman－Kolmogorov方程得

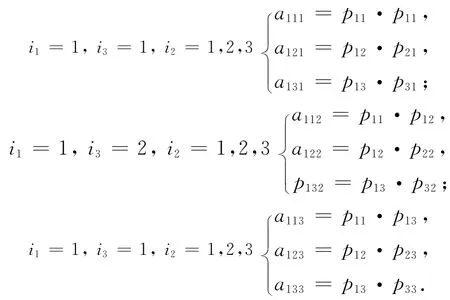
由P 的行和为1得

第三步：固定i3指标，令i3＝1（当i3＝2，i3＝3时同理）．由P 的列和为1得

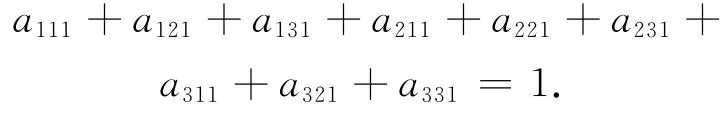
可知A ＝（ai1i2i3）为超随机张量．类似可得，当齐次马氏链状态集为E ＝｛1，2，…，n｝时，相应地转移过程张量A 为3阶n维时，即当阶数k＝3时，命题成立．

当k＝m，j＝1时，

当k＝m，j＝m 时，

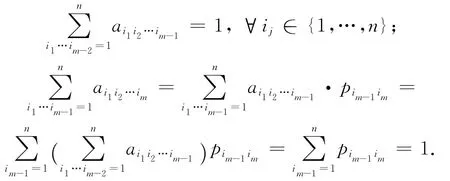
证毕．

进一步，这里是借助马氏链的状态转移过程定义了张量，实际上是由P（矩阵）所生成的，结果表明：当马氏链的一步转移概率矩阵为双随机矩阵时，其m－1步转移过程张量为超随机张量．当然，另一方面也不难知道，超对称的随机张量都是超随机张量．下面，将进一步探讨什么样的张量会是超随机张量．

定理3 假设m 阶n 维张量A ＝（ai1i2…im）是由n维向量x＝（x1，…，xn）T生成的，即ai1i2…im＝xi1·xi2…xim．若x1＝x2＝…＝xn＝n1－mm，则A为超随机张量．

2 超随机张量的几个简单性质

文献［9－16］研究了许多关于特殊张量的性质．由于超随机张量是一类特殊的随机张量，故而它也满足随机张量的性质［5］．易见，超随机张量有如下性质：

性质1 若A 为m 阶n 维超随机张量，则有：

1）λ＝1为A的一个特征值，e＝［1…1］T为A的对应于λ＝1的一个特征向量．

2）ρ（A）＝1，这里ρ（A）为A 的谱半径，即特征值的最大值．

3）若A 为不可约的，则λ＝1为单重特征值．

该性质表明，超随机张量具有随机张量的性质．当然，作为一种特殊的随机张量，超随机张量具有更好的性质．

性质2 若A 为m 阶n 维超随机张量，则有：

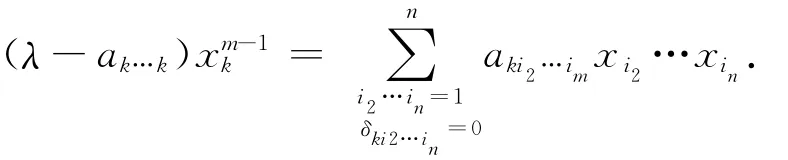
可知，

由于A 为超随机张量，故而

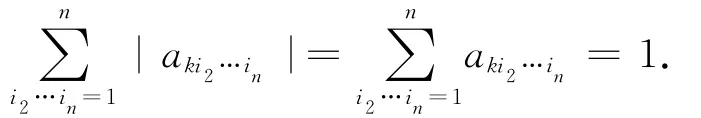
［1］Qi Liqun．Eigenvalues of a real supersymmatric tensor［J］．Journal of Symbolic Computation，2005，40（1）：1302－1324．

［2］Qi Liqun．Rank and eigenvalues of a surpersymmetric tensors，the multivariate homogeneous polynomial and the algebraic hypersurface it defines［J］．Journal of Symbolic Computation，2006，41（1）：1309－1327．

［3］Chang K C，Pearson K，Zhang T．On eigenvalue problems of real symmetric tensors［J］．J Math．Anal．Appl．，2009，350（1）：416－422．

［4］Chang K C，Pearson K，Zhang T．Primitivity，the convergence of the NQZ method，and the largest eigenvalue for nonnegative tensors［J］．SIAM J．Matrix Anal．Appl．，2011，32（1）：806－819．

［5］Yang Qingzhi，Yang Yuning．Further results for perron－frobenius theorem for nonnegative ten－sors 2［J］．Society for Industrial and Applied Mathematrics，2011，32（4）：1236－1250．

［6］Chang K C，Pearson K，Zhang T．Perron－frobenius theorem for nonnegative tensor［J］．Commun．Math．Sci．，2008，6（2）：507－520．

［7］Yang Yuning，Yang Qingzhi．Further results for perron－frobenius theorem for nonnegative ten－sors［J］．Society for Industrial and Applied Mathematrics，2010，31（5）：2517－2530．

［8］陆大金．随机过程及其应用［M］．北京：清华大学出版社，2012．

［9］Ng M，Qi Liqun，Zhou Guanglu．Finding the largest eigenvalue of a non－negative tensor［J］．SIAM J．Matrix Anal．Appl．，2009，31（3）：1090－1099．

［10］Chang K C，Qi Liqun，Zhou Guanglu．Singular values of a real rectangular tensor［J］．Math．Anal．Appl．，2010，370（1）：284－294．

［11］Yang Yuning，Yang Qingzhi．Singular values of nonnegative rectangular tensors［J］．Front．Math．China，2011，6（2）：363－378．

［12］Kolda T G，Bader B W．Tensor decompositions and applications［J］．SIAM Review，2009，51（3）：455－500．

［13］Chang K C，Pearson K，Zhang T．Some variational principles for Z eigenvalues of nonnegative tensors［J］．Linear Algebra and its Applications，2013，438（1）：4166－4182．

［14］Qi Liqun，Wang Fei，Wang Yiju．Z－eigenvalue methods for a global polynomialo ptimizationproblem［J］．Math．Program．Ser．A，2009，118（1）：301－316．

［15］Liu Yongjun，Zhou Guanglu，Nur F I．An always convergent algorithm for the largest eigenvalues of an irreducible nonegative tensor［J］．Journal of Computational and Applied Mathematics，2010，235（1）：286－292．

［16］Qi Liqun．Symmetric nonnegative tensors and copositive tensors［J］．Linear Algebra and its Applications，2013，439（1）：228－238．