与Bullen不等式有关的若干不等式
时统业,周国辉
(海军指挥学院信息系,江苏 南京 211800)
与Bullen不等式有关的若干不等式
时统业,周国辉
(海军指挥学院信息系,江苏 南京 211800)
首先建立涉及三阶导数的积分恒等式,然后使用Hölder不等式和Grüss不等式的变式,得到三阶可微函数与Bullen不等式有关的一些不等式.
凸函数;Hölder不等式;Grüss不等式;Bullen不等式
设区间I⊂R,函数f:I⊂R→R,如果对任意x,y∈I及λ∈[0,1]有
f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y),则称f是区间I上的凸函数.
若f是区间I上的凸函数,a,b∈I,a<b,则凸函数的Hermite-Hadamard不等式[1]和Bullen不等式[2]分别为下面的式(1)和式(2)

下面的Fejér-Hermite-Hadamard不等式[3]是Hermite-Hadamard不等式的加权推广

其中函数f是[a,b]上的凸函数,g(x)是[a,b]上关于x=(a+b)/2对称的非负可积函数.
Grüss不等式[1]设h,g是定义在[a,b]上的两个可积函数,且满足φ1≤h(x)≤Φ1,γ1≤h(x)≤Γ1,x∈[a,b],则有
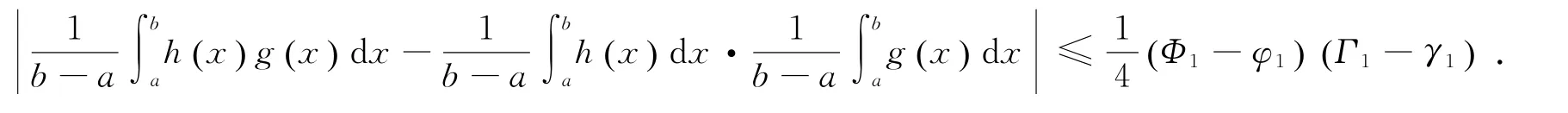
文献[4]给出下面Grüss不等式的变式:
引理1[4]设h,g是定义在[a,b]上的两个可积函数,且满足φ≤g(x)≤Φ,x∈[a,b],其中φ和Φ是常数,则有

文献[5]首先建立与Bullen不等式有关的恒等式,然后使用Hölder不等式、Grüss不等式以及Chebychev不等式,得到二阶可微函数的一些不等式.
引理2[5]设f:I⊂R→R是I°(I的内部)上的二阶可微函数,a,b∈I°,a<b,f″在[a,b]上勒贝格可积,则有
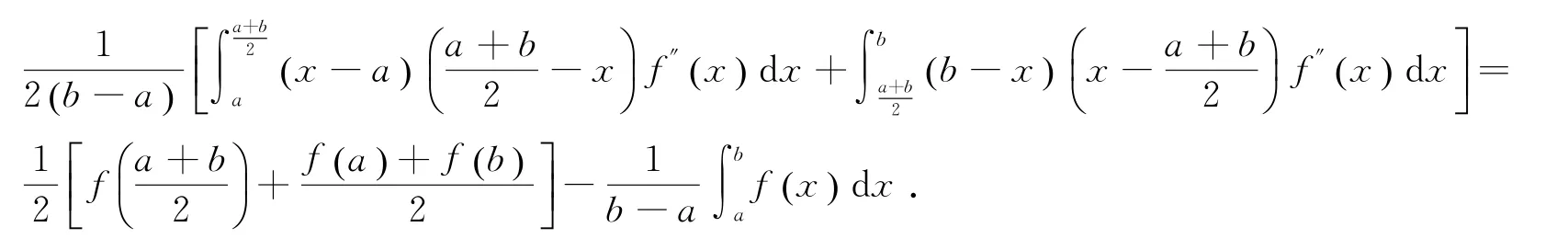
笔者将仿照文献[5]的方法,首先建立与Bullen不等式有关的恒等式,然后使用Hölder不等式和Grüss不等式,得到三阶可微函数的一些不等式.
1 主要结果
引理3 设有I°上的三阶可微函数f:I⊂R→R,a,b∈I°,a<b,f‴在[a,b]上勒贝格可积,则有

其中

证明使用分部积分法得
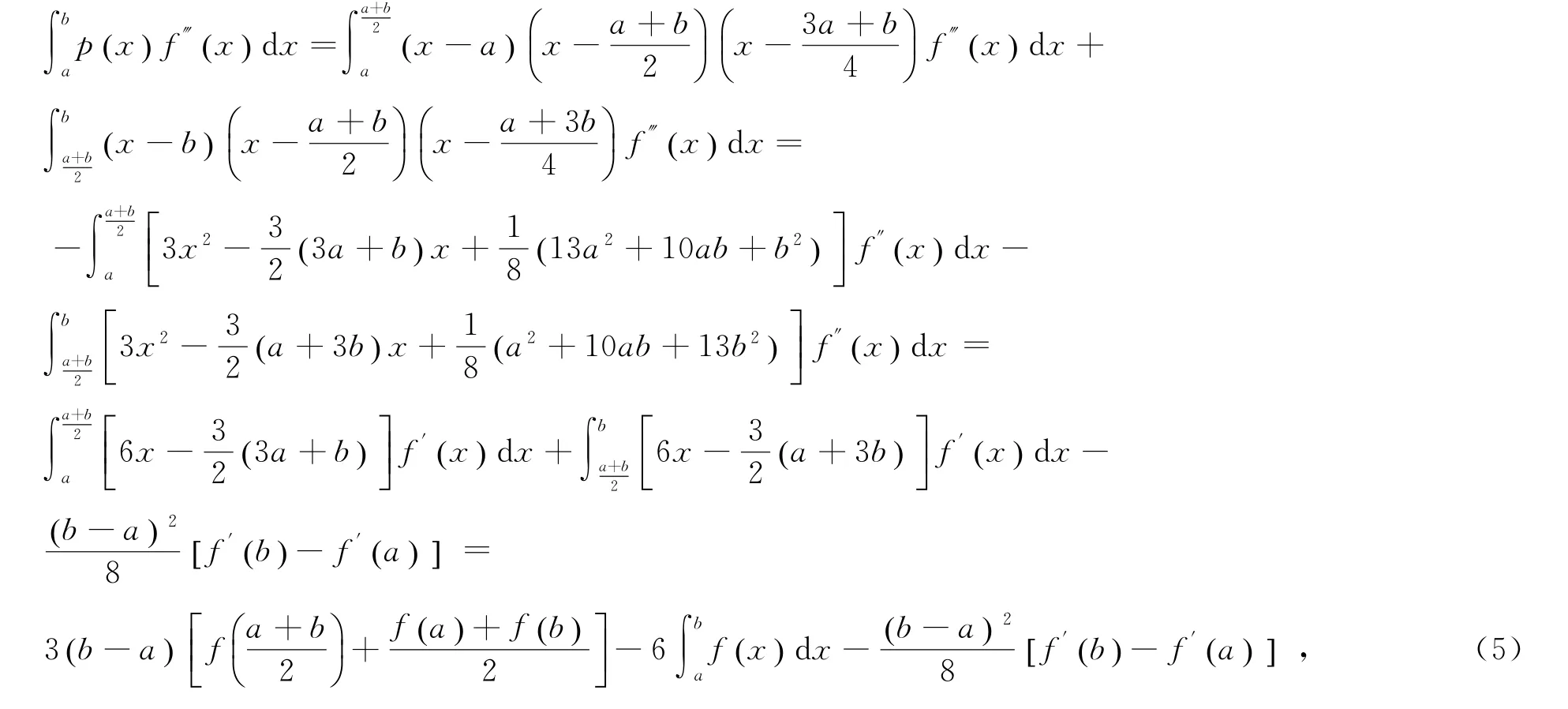
式(5)除以6(b-a),得到式(4),引理1证毕.
易见函数p(x)关于x=(a+b)/2对称,在[a,(3a+b)/4]上有p1(x)≥0,在[(3a+b)/4,(a+ b)/2]上有p1(x)≤0,在[(a+b)/2,(a+3b)/4]上有p2(x)≤0,在[(a+3b)/4,b]上有p2(x)≥0,利用分部积分法计算可得
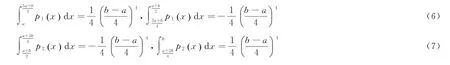
从而有
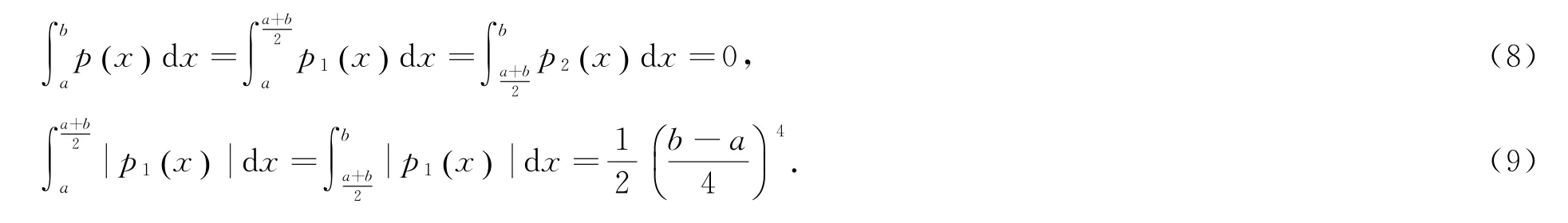
定理1 设f:I⊂R→R是I°上的三阶可微函数,a,b∈I°,a<b,f‴在[a,b]上勒贝格可积,若是[a,b]上的凸函数,则有

证明注意到函数|p(x)|关于x=(a+b)/2对称,故由引理2及式(3)得

因为|p1(x)|关于x=(3a+b)/4对称,是凸函数,故由式(3)得

因为|p2(x)|关于x=(a+3b)/4对称,是凸函数,故由式(3)得

由式(9)、(11)、(12)、(13)得到式(10),定理1证毕.
定理2 设f:I⊂R→R是I°上的二阶可微函数,a,b∈I°,a<b,f‴在[a,b]上勒贝格可积,若在[a,(3a+b)/4)上有γ1≤f‴(x)≤Γ1,在[(3a+b)/4,(a+b)/2)上有γ2≤f‴(x)≤Γ2,在[(a+ b)/2,(a+3b)/4)上有γ3≤f‴(x)≤Γ3,在[(a+3b)/4,b]上有γ4≤f‴(x)≤Γ4,则有

证明由引理2及式(6)、(7)得

类似可证

于是式(14)得证.
注1 存在函数f(x)在四个区间[a,(3a+b)/4)、[(3a+b)/4,(a+b)/2)、[(a+b)/2,(a+ 3b)/4)、[(a+3b)/4,b]上分别具有三阶导数,且在这四个区间上的三阶导数分别为Γ1、γ2、γ3、Γ4,使得式(14)的右边等号成立.还存在满足定理2条件的函数使得式(14)的左边等号成立.
推论1 设f:I⊂R→R是I°上的三阶可微函数,a,b∈I°,a<b,f‴在[a,b]上勒贝格可积,若对任意x∈[a,b]⊂I°有γ≤f‴(x)≤Γ,则有

定理3 设f:I⊂R→R是I°上的三阶可微函数,a,b∈I°,a<b,|f‴|在[a,b]上勒贝格可积,p>1,则有
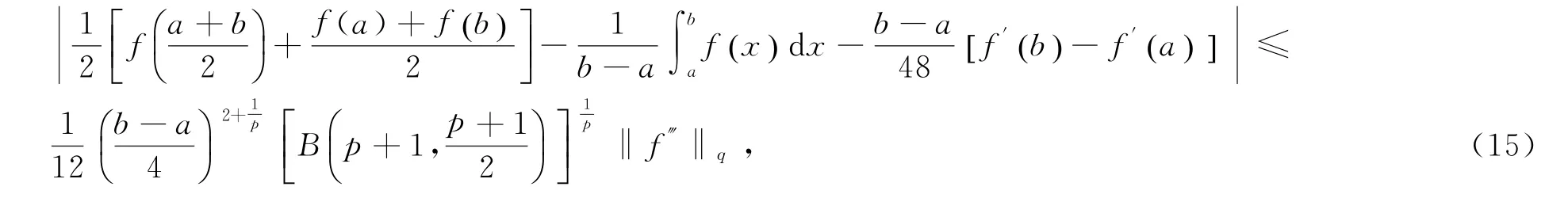
证明由引理2及Hölder不等式得
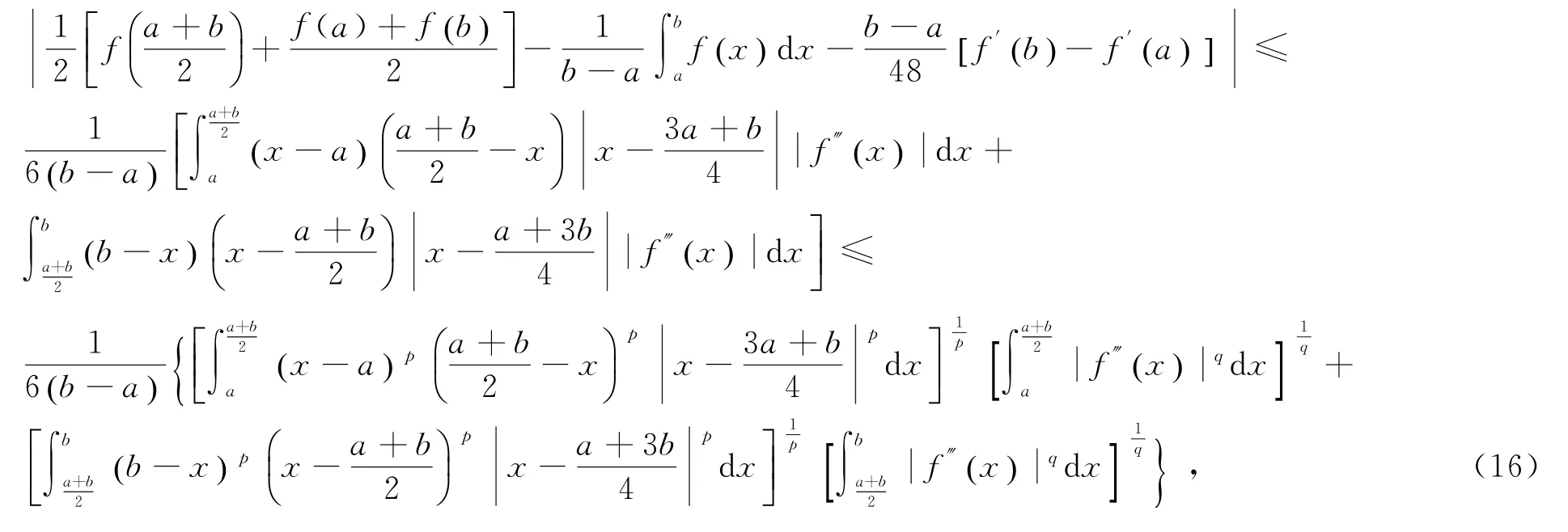

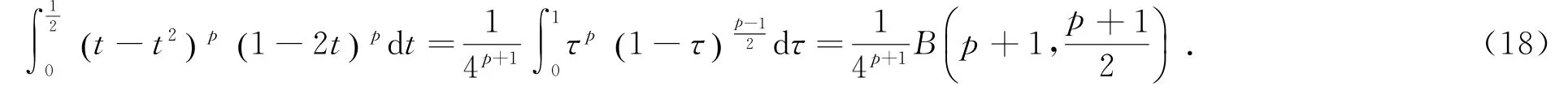
作变量代换x=a+b-u得

由式(16)、(17)、(18)、(19)证得式(15).
注2 当p=2时,由式(15)得

定理4 设f:I⊂R→R是I°上的二阶可微函数,a,b∈I°,a<b,在区间[a,(a+b)/2)上满足γ1≤f‴(x)≤μ1,在区间[(a+b)/2),b]上满足γ2≤f‴(x)≤μ2,若f‴在[a,b]上勒贝格可积,则有

证明由引理1不等式得

类似可证

由式(21)、(22)得

式(23)乘以1/12并利用引理2及式(8),可得式(20),定理4证毕.
注3 道理同注1,式(20)是严格的.
2 应用
两个相异实数α,β的调和平均、算术平均、广义对数平均分别为

性质1 设0<a<b,n∈Z,n≤-2或n≥5,则有

证明设定义在(0,∞)上的函数f(x)=xn,n∈Z,n≤-1或n≥5,则=|n(n-1)(n-2)|xn-3是凸函数,对f(x)应用定理1的式(10),性质1得证.
性质2 设0<a<b,则有

证明设定义在(0,∞)上的函数f(x)=x-2,则f‴(x)=-24x-5,并且有

对f(x)应用定理4的式(20),性质2得证.
[1]Mitrinovi c′D S.Analytic inequalities[M].Springer-Verlag New-York,Heidelerg,Berlin,1970:70.
[2]Dragomir S S,Pearce C E M.Selected Topics on Hermite-Hadamard inequalities and applications[DB].http://rgmia.vu.edu.au/SSDragomirweb.html.
[3]Fejér L.Über die Fourierreihen,II,Math.[J].Naturwiss,Anz.Ungar.Akad.Wiss.,1906(24):369-390.
[4]Cheng X L,Sun J.A note on the perturbed trapezoid inequality[J].J.Inequal.Pure Appl.Math.,2002,3(2):29.
[5]Kirmaci U S,Dikici R.On some Hermite-Hadamard type inequalities for twice differentiable mappings and applications [J].Tamkang J.Math.,2013,44(1):41-45.
Some inequalities relating to bullen’s inequality
SHI Tongye,ZHOU Guohui
(Department of Information,PLA Naval Command College,Nanjing 211800,China)
A general integral identity relating to Bullen’s inequality for three order differentiable mappings is derived.Some inequalities for three order differentiable mappings are presented by using Hölder’s inequality and Grüss’s inequality.
convex functions;Hölder’s inequality;Grüss’s inequality;Bullen’s inequality
O178
:A
:1671-9476(2015)05-0024-06
10.13450/j.cnkij.zknu.2015.05.007
2015-03-17;
:2015-04-20
时统业(1963-),男,河北张家口人,副教授,硕士,从事基础数学教学和研究.

