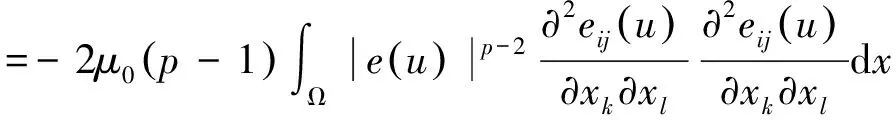非牛顿流无粘极限的进一步研究
崔帆, 郭春晓
(中国矿业大学 理学院,北京 100083)
1 引 言
在航空、化学及石油等众多工业领域中,有关流体运动数学模型的理论和计算研究正引起广泛关注.基于Stokes的假设,流体的Navier-Stokes模型限制了应力张量与速率梯度间的线性关系[1-3].满足这一本构关系的流体称为牛顿流,如水和空气.但是诸如生物流体、合成纤维等流动行为不能用牛顿关系来描述的流体材料就要建立非牛顿流体数学模型.
本文具体考虑如下在二维周期域上的等温双极不可压粘性非牛顿流系统:
ut+u·u-·(γ(u)e(u))+μ1Δ2u-νΔu=-P+f(x),(x,t)∈Ω×[0,T]
(1)
·u(x,t)=0,x∈Ω
(2)
u(x,0)=u0(x)
(3)

(4)
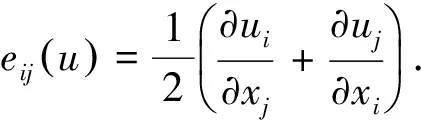
当μ0=μ1=0时,方程(1)变为Navier-Stokes方程[2-3],系统如下:
vt+v·v-νΔv=-
(5)
·v(x,t)=0,x∈Ω
(6)
v(x,0)=v0(x)
(7)
(8)

本文在已知非牛顿流的解u(x)和Navier-Stokes方程解v(x)及具有合适相同初始值的前提下,考虑两系统解的差w(x)=u(x)-v(x)在不同范数意义下的估计.文献[4]中得到了两系统在给定合适的初始条件下1 为了方便描述,C是一个通用的常数,并假设每一行都代表不同的值,且在本文中均不依赖于粘性系数μ0、μ1. 首先定义一个H1(Ω)×H1(Ω)×H1(Ω)上的连续三线性函数如下: 易知:b(u,v,w)=-b(u,w,v),b(u,v,v)=0. 利用Galerkin逼近和一些先验估计可以得到解的存在唯一性,这一方法是经典的,更多的细节可以参考文献[5-7]. 下面列出了在文献[4]中μ0≠μ1时本文将要使用到的一些结论: u0∈H1(Ω),v0∈H1(Ω),f∈H,p>1时,存在常数C使得 ‖u(t)‖≤C,‖Δu(s)‖2ds≤C,‖v(t)‖≤C,‖Δv(s)‖2ds≤C v0∈V,f∈H1(Ω) 时,存在常数C使得 证明对(1)式和Δ2u在H中取内积,有 (9) (10) (11) 应用Gagliardo-Nirenberg不等式有 (12) 又计算可得 (13) 结合估计(9)、(11)和(12),有 (14) 对(14)式两边从0到t积分,则得结论. 定理3.1 给定相同的初始值u0=v0∈V,对有限时刻t∈[0,T],存在常数C使得w(x,t)遵循如下估计: (15) ‖ (16) 证明w(x,t)满足如下方程: w(t)+u·w+w·v-νΔw= (17) 对(15)式和w在H中做内积.由于散度为零,有b(u,w,w)=0,从而 对上述等式的右端逐项估计 μ1|(Δ2u,w)|≤μ1‖Δw‖‖Δu‖≤Cμ1(‖Δv‖2+‖Δu‖2) (18) (19) (20) 结合上述估计,得到以下不等式 应用Gronwall不等式,有 类似地,对(15)式和-Δw在H中做内积 (21) (22) 结合文献[4]中的估计有 (23) (24) 得到 同理应用Gronwall不等式,即得(14)式. 定理3.2 令u0=v0∈V,则差w(x,t)对有限时刻t∈[0,T]有如下估计: 证明应用Gagliardo-Nirenberg不等式有 则 (25) [1] ROBINSON J C.Infinite-dimensional dynamical systems: an introduction to dissipative parabolic PDEs and the theory of global attractors[M].Cambridge:Cambridge Uni.Press,2001. [2] TEMAM R.Navier-Stokes equations: theory and numerical analysis[M].3rd Revised Edition.Amsterdan:North Holland Pub.Co.,1984. [3] TEMAM R.Infinite dimensional dynamical systems in mechanics and physics[M].2nd Edition.New York:Springer-Verlag New York Inc.,1997. [4] GUO B L,GUO C X.The convergence of non-Newtonian fluids to Navier-Stokes equations[J].J.Math.Anal.Appl.,2009,357(2):468-478. [5] BELLOUT H,BLOOM F,NECAS J.Weak and measure-valued solutions for non-Newtonian fluids[J].C.R.Acad.Sci.Pairs,1993,317:795-800. [6] BELLOUT H,BLOOM F,NECAS J.Young measure-valued solutions for non-Newtonian incompressible viscous fluids[J].Comm.Partial Differential Equation,1994,19(11-12):1763-1803. [7] BLOOM F,HAO W.Regularization of a non-Newtonian system in an unbounded channel:existence and uniqueness of solutions[J].Nonlinear Anal.,2001,44(3):281-309.2 预备知识
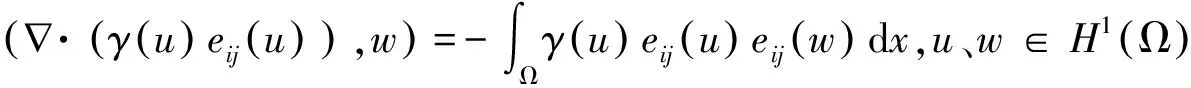
3 解的收敛性