基于hp自适应伪谱法的多脉冲导弹弹道优化设计①
明 超,孙瑞胜,白宏阳,孙传杰
(1.南京理工大学 能源与动力工程学院 ,南京 210094;2.工程物理研究院总体工程研究所,绵阳 621900)
基于hp自适应伪谱法的多脉冲导弹弹道优化设计①
明 超1,孙瑞胜1,白宏阳1,孙传杰2
(1.南京理工大学 能源与动力工程学院 ,南京 210094;2.工程物理研究院总体工程研究所,绵阳 621900)
针对多脉冲导弹非连续助推的特点,基于hp自适应伪谱法研究了多约束多阶段的弹道优化设计问题。结合多脉冲导弹的工作过程,给出了弹道的分段准则, 在考虑过载、动压及终端弹道参数等约束条件下,建立了运动学模型以及多约束多阶段全弹道优化模型。为解决Radau伪谱法处理复杂优化问题时存在的局限性,提出了一种基于hp自适应伪谱法的求解策略,对其最大射程的弹道进行了优化设计,并与传统的最大升阻比方案所得的结果进行了比较分析。仿真结果表明,该方法能有效解决多脉冲导弹弹道优化问题,射程比最大升阻比方案提高了7.8%,研究结果可为多脉冲导弹的弹道总体设计提供参考。
多脉冲导弹;弹道优化;最大射程;hp自适应伪谱法
0 引言
在未来战争中,随着作战范围和作战空间的逐渐扩大,对导弹的飞行性能提出了更高的要求。多脉冲导弹通过调节各脉冲发动机之间的间隔时间,来减少导弹空气阻力消耗,改善导弹的机动性能,增加导弹的射程,提高导弹的生存能力。其中,具有代表性的是德国近距离内防空导弹LFK-NG和美国防区外发射的近程攻击导弹SRAM-A[1-2]。为了充分发挥多脉冲弹飞行性能的优势,对多脉冲导弹进行弹道优化具有重要的理论研究意义和工程应用价值。
多脉冲导弹弹道优化问题是一个始端固定、终端时刻自由且含有路径约束和终端约束的多阶段最优控制问题[3]。一般轨迹优化数值方法,主要包括直接法和间接法[4]。由于间接法在求解过程中还存在诸多不足,近年来直接法广泛用于各种轨迹优化问题[5-6]。伪谱法为直接法最活跃的分支,由于具有结构简单、精度高及收敛速度快的特点,且使得非线性规划(NLP)的解满足传统间接法的一阶最优性必要条件,而备受关注[7-9]。但在处理一些复杂问题时也呈现出一定的局限性。hp自适应伪谱法[10]是将伪谱法与hp型有限元法结合,在计算过程中对配点数和插值多项式的阶次进行自适应调整,以满足计算精度的要求。
本文以双脉冲导弹作为研究对象,以脉冲发动机二次点火时间和飞行攻角为优化变量,考虑优化变量约束,并对终端速度和落角进行一定的限制,采用hp自适应伪谱法,对双脉冲导弹最大射程进行弹道优化研究,并与最大升阻比方案所得的结果进行比较分析。
1 弹道优化问题描述
1.1 双脉冲导弹工作过程
双脉冲导弹的飞行过程可分以下4个阶段:第一阶段,脉冲发动机第一次工作,将导弹加速到一定的速度后关机;第二阶段,导弹无动力飞行,此时导弹速度不大,阻力所消耗的能量小;第三阶段,导弹到达高空后,发动机第二次工作,速度增加到末段机动飞行所需值;第四阶段,导弹无动力滑翔直至目标。其工作过程示意图如图1所示。
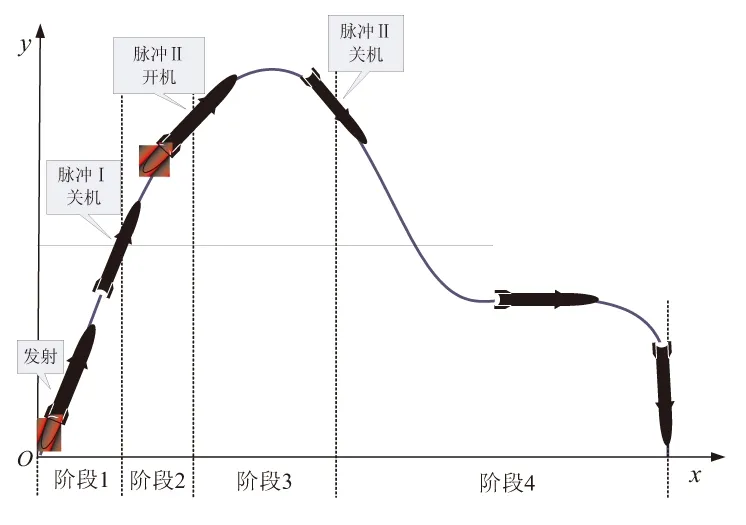
图1 双脉冲导弹工作过程示意图Fig.1 Schematic diagram of double-pulse missile working process
1.2 动力学模型
为了便于研究问题,本文只考虑多脉冲导弹纵向平面内的运动,假设地球表面为平面且忽略地球自转的影响。多脉冲导弹的动力学模型为
(1)
式中m为导弹质量;P为发动机推力;X=qSCx、Y=qsCy分别为阻力和升力,由动压q和气动特性决定,其中Cx和Cy是Ma和α的函数,可由吹风试验和数值计算获得;θ为弹道倾角;其他符号及具体表达式详见文献[11]。
1.3 约束条件
(1)边界条件
双脉冲导弹的初始状态:
v(0)=v0,θ(0)=θ0,x(0)=x0
y(0)=y0,m(0)=m0
为了保证双脉冲导弹的攻击效果,终端弹道参数应满足一定的约束,包括终端位置、速度和落角约束,即
vfmin≤v(tf)≤vfmax
θfmin≤θ(tf)≤θfmax
y(tf)=yf
(2)连接点约束
为使双脉冲导弹飞行的4个阶段间平滑过渡,保证上一阶段结束时刻的状态量、控制量与下一阶段开始时刻的对应相等[12],约束条件为
t0(i+1)=tf(i),s0(i+1)=sf(i),
u0(i+1)=uf(i),(i=1,2,3)
式中i为双脉冲导弹飞行的第i阶段;t为时间;s为状态量;u为控制量;下标0、f表示开始、结束。
(3)控制约束
双脉冲导弹的脉冲发动机二次点火时间t02和飞行攻角α的约束条件为
(4)路径约束
1.4 目标函数
对于双脉冲导弹总体设计初步阶段,一个重要的目标就是双脉冲导弹按照预定的方案飞行的射程最远。因此,弹道优化设计的目标函数为
minJ=-x(tf)
(2)
2 hp自适应伪谱法
本文所采用的hp自适应伪谱法是将Radau伪谱法[13]与hp型有限元法进行融合,在一系列离散点上,利用全局多项式近似微分方程约束,从而将最优控制问题的求解转化为对NLP问题的求解,其离散过程与Radau伪谱法相似。当某一离散区间的计算精度不满足要求时,由hp自适应方法对该区间内的配点数h和全局插值多项式的阶次p进行自适应调整。当然,hp自适应伪谱法也可使用其他伪谱法(如Legendre伪谱法,Gauss伪谱法等)离散最优控制问题,Radau伪谱法的优点是容易满足网格点的连续条件[13]。
2.1 最优控制问题离散
Radau伪谱法对多脉冲导弹弹道优化最优控制问题的离散过程如下。
将最优控制问题的为t∈[t0,tf]划分为K个网格,且将时间区间转换至τ∈[-1,1],做映射变换有
(3)
式中 ∀t∈[tk-1,tk],k=1,…,K,t0<… 状态量在第k(k∈[1,…,K])个网格近似表示为 (4) (5) 将X(k)(τ)对τ求导,代入动力学微分方程式,并在LGR点上进行离散,可得 (6) 目标函数可近似表示为 (7) 不等式约束在第k个网格上用Nk个LGR点离散化处理,有 (8) 边界约束条件可近似表示为 (9) 为了保证网格的连续性,需满足: (10) 基于上述的离散过程,Radau伪谱法将多脉冲导弹弹道优化最优控制问题转化为非线性规划问题,可以利用求解NLP问题的SNOPT[14]等软件包,对其进行求解。 2.2 hp自适应更新判定准则 2.3 hp自适应更新方式判定准则 (11) (12) 如果rk 2.4 hp自适应更新变量计算公式 (1)更新后插值多项式的阶次Dnew (13) (2)更新后配点数Mnew (14) 式中Mnew为更新后网格内的配点数;B为用户自定义参数。 2.5 hp自适应伪谱法计算流程 hp自适应伪谱法计算步骤如下所示,其流程图如图2所示。 (1)按照划分好的网格,利用Radau伪谱法将最优控制问题离散,转化为NLP问题,并采用序二次规划法对NLP问题进行求解; Begin:fork=1,2,…,K (3)如果rk End:fork=1,2,…,K (4)如果状态量和路径约束的相对误差满足允许的相对误差,则优化结束;不满足,则返回步骤(1)。 图2 hp自适应伪谱法流程图Fig.2 Flow chart of hp-adaptive pseudo-spectralmethod 表1 优化结果比较Table1 Comparison of optimization results 由仿真结果可看出,在给定的仿真条件下,采用hp自适应伪谱法优化后,双脉冲导弹的发动机二次点火时间为26 s,攻角曲线平滑,所有的设计约束条件均能满足,最大射程较传统的最大升阻比滑翔方案提高了7.8%,说明该方法能够获得较优的弹道。在普通的PC机上,hp自适应伪谱法优化计算的时间为30 s左右,表明该方法具有较高的计算效率。仿真验证了该方法处理多脉冲导弹飞行过程中状态量以及控制量不连续问题的可行性。 图3 弹道曲线Fig.3 Curves of ballistic 图4 速度变化曲线Fig.4 Change curves of velocity 图5 弹道倾角变化曲线Fig.5 Change curves of trajectory inclination angle 图6 攻角变化曲线Fig.6 Change curves of angle of attack 图7 法向过载变化曲线Fig.7 Change curves of normal acceleration 图8 动压变化曲线Fig.8 Change curves of dynamic pressure (1)针对多脉冲导弹弹道优化问题,建立了多阶段、多约束的弹道优化模型,引入连接点约束条件处理各阶段状态量、控制量的不连续问题,方法简单,且效果好。仿真结果表明,所建立的优化模型是合理的。 (2)为解决Radau伪谱法在处理复杂优化问题时存在的局限性,提出了一种基于hp自适应伪谱法的求解策略,并以射程最大为性能指标,对多脉冲导弹多阶段多约束弹道进行了优化设计。仿真结果表明,hp自适应伪谱法能有效解决多脉冲导弹弹道优化问题,具有较高的计算效率,优化方案的射程比传统的最大升阻比飞行方案提高了7.8%,在提高射程方面具有明显优势。 (3)研究结果能提供近实时最优解,可为多脉冲导弹制导律的优化设计和轨迹的在线生成提供一定的参考。 [1] Naumann K W,Stadler L J.Double-pulse solid rocketmotor technology-applications and technical solutions[C]//the 46th AIAA/ASME/SAE/ASWW,2010.2345-2353. [2] 龚世杰,戴耀松.多脉冲固体火箭发动机述评[J].飞航导弹,1993(1):32-39. [3] 唐国金,罗亚中,雍恩米.航天器轨迹优化理论、方法及应用[M].北京:科学出版社,2012. [4] Betts J T.Survey of numerical methods for trajectory optimization[J].Journal of Guidance,Control and Dynamics,1998,21 (2):193-206. [5] Benson D A,Huntington,G T,Thorvaldsen T P,et al.Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1435-1440. [6] 陈聪,关成启,史宏亮. 飞行器轨迹优化的直接数值解法综述[J].战术导弹控制技术,2009,31(2):33-40. [7] Gong Q,Kang W,Ross I S.A pseudo-spectral method for optimal control of constrained feedback linearizable systems[J].IEEE Transaction on Automatic Control,2006,51(7):1125-1129. [8] Williams P.Application of pseudo-spectral methods for receding horizon control[J].Journal of Guidance,Control,and Dynamics,2004,27(2):310-314. [9] Rao A V,Garg D,Hager WW.Pseudo-spectral method for solving infinite-horizon optimal control problems[J].Automatic,2011,47(4): 829-837. [10] Darby C L,Hager W W,Rao A V.An hp-adaptive pseudo-spectral method for solving optimal control problems[J].Optimal Control Applications and Methods,2011,32(4):476-502. [11] 钱杏芳,林瑞雄,赵亚男. 导弹飞行力学[M].北京理工大学出版社,2000. [12] Rao A V,Benson D A,Darby C L,et al. Algorithm 902:GPOPS,A MATLAB Software for solving multiple-phase optimal control problems using the gauss pseudo-spectral method [J].ACM Transactions on Mathematical Software,2010,37(2):22:1-22:39. [13] Darby C L,Hager W W,Rao A V. Direct trajectory optimization using a variable low-order adaptive pseudo-spectral method[J].Journal of Spacecraft and Rockets,2011,48(3):433-445. [14] Gill P E,Murray W,Saunders M A.SNOPT:an SQP algorithm for large scale constrained optimization[J].SIAM Journal on Optimization,2002,12(4):979-1006. (编辑:吕耀辉) Optimizing design of trajectory for multiple-pulse missiles based on hp-adaptive pseudo-spectral method MING Chao1,SUN Rui-sheng1,BAI Hong-yang1,SUN Chuan-jie2 (1.School of Energy and Power Engineering, NUST,Nanjing 210094, China;2.Institute of Systems Engineering,CAEP,Mianyang 621900,China) According to the characteristics of the discontinuous boost for multiple-pulse missiles, the multi-constraints and multi-phase trajectory optimization problem based on hp-adaptive pseudo-spectral method was researched.The trajectory segment criterion was presented combining with the missile working process.The dynamic model and multi-constraints multi-phases trajectory optimization model were established concerning the constraints of overload,dynamic pressure,and terminal trajectory parameters.A maximum range optimization calculation case based on hp-adaptive pseudo-spectral method solving strategy was given,so as to tackle the constraints when using Radau,pseudo spectral method to deal with complicated optimization problem.Moreover,the results were compared with that of the traditional maximum lift-to-drag ratio method.The simulation results show that the algorithm can efficiently solve the problem of multiple-pulse missile trajectory optimization and improve the maximum range by 7.8% in comparison to the maximum lift-to-drag ratio method. The results can provide a reference to the overall design of multiple-pulse missiles. multiple-pulse missiles;trajectory optimization;maximum range;hp-adaptive pseudo-spectral method 2014-04-03; :2014-05-16。 国家自然科学基金委员会和中国工程物理研究院联合基金(11176012);航天一院高校联合创新基金(CALT201302)。 明超(1989—),男,博士,研究方向为先进弹道优化理论与控制技术。E-mail:mcnust@126.com 孙瑞胜(1976—),男,副教授,研究方向为新型弹箭制导与控制技术。E-mail:srscom@163.com V412.4 A 1006-2793(2015)02-0151-05 10.7673/j.issn.1006-2793.2015.02.001
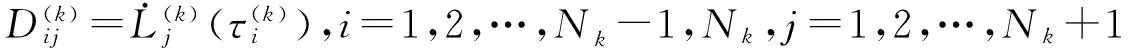
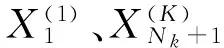
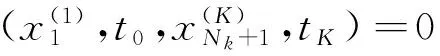



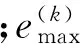
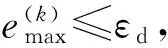

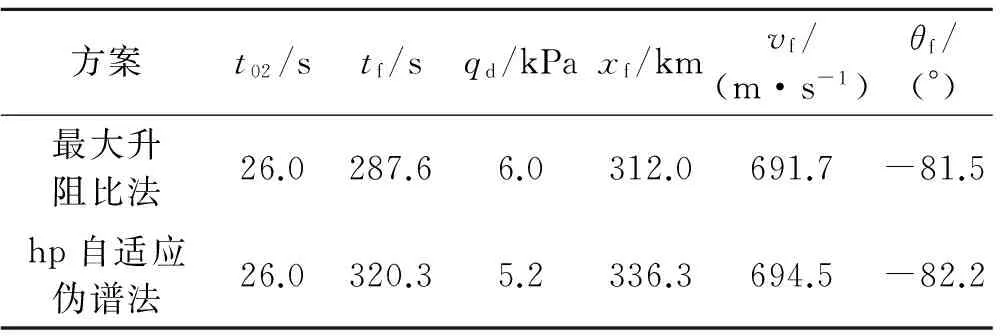
3 仿真分析
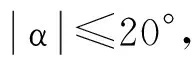

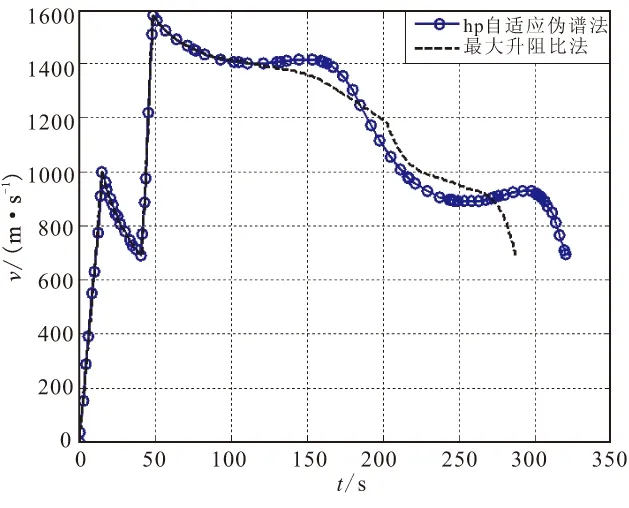
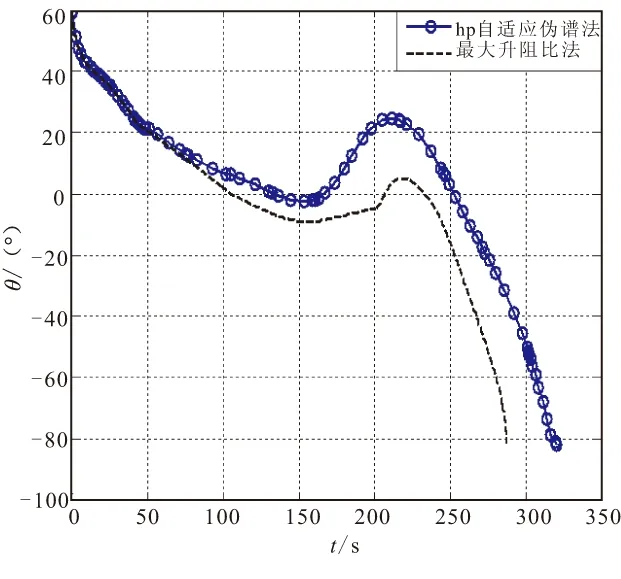
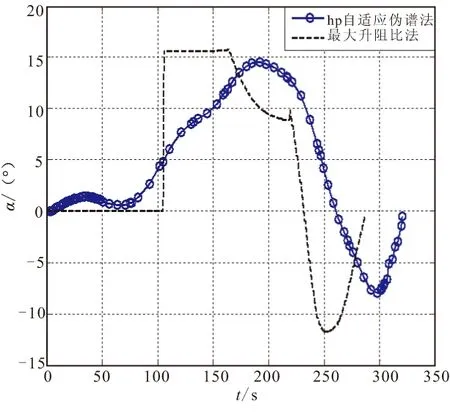
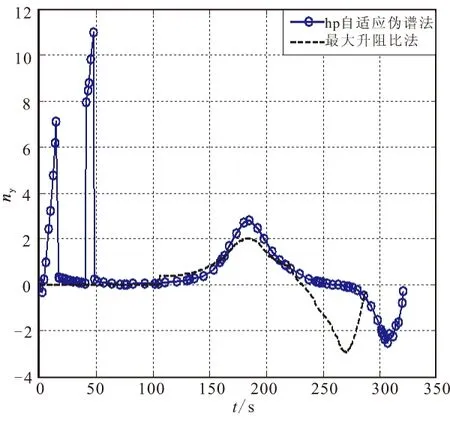
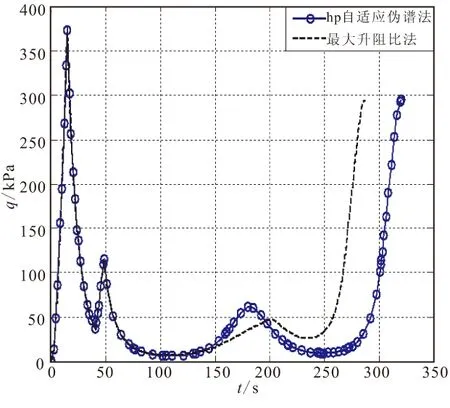
4 结论

