A Hilbert-Type Integral Inequality with the Inhomogeneous Kernel and Multi-Parameters
,
(1.Preparatory Department of Primary Education, Changsha Normal University, Changsha 410100;2.Department of Science and Information, Shaoyang University,Shaoyang 422000 China)
A Hilbert-Type Integral Inequality with the Inhomogeneous Kernel and Multi-Parameters
HUANGLin1*,LIUQiong2
(1.Preparatory Department of Primary Education, Changsha Normal University, Changsha 410100;2.Department of Science and Information, Shaoyang University,Shaoyang 422000 China)
In this paper, by means of weight function and the technique of real analysis, and introducing multi-parameters and some special functions to jointly characterize the constant factor, a Hilbert-type integral inequality with the inhomogeneous kernel and multi-parameters and it’s equivalent form are given. Their constant factors are proved be the best possible, and its application is discussed.
Hilbert-type integral inequality; weight function; the best constant factor; inhomogeneous kernel; multi-parameters
1 Introduction
For convenience, Ifθ(x)(>0)ismeasurablefunction,ρ≥1,thefunctionspacesaresetas:
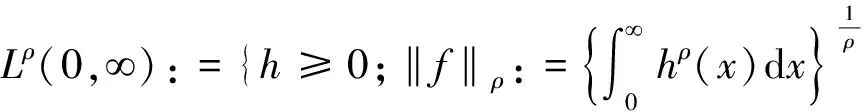
and
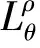
Iff,g∈L2(0,),‖f‖2,‖g‖2>0,thenwehavethefollowingHilbert’sintegralinequality[1]:

(1.1)
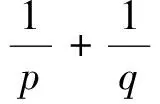

(1.2)
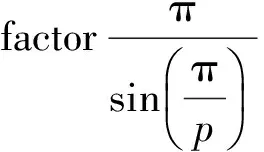

(1.3)

(1.4)
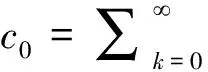
Inthispaper,bymeansofweightfunctionandthetechniqueofrealanalysis,aHilbert-typeintegralinequalitywiththeinhomogeneouskernelandMulti-parametersisgivenasfollows:
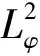

(1.5)
2 Some Lemmas
We need the following definitions[11]:
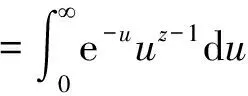
(2.1)
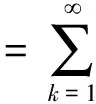
(2.2)
Lemma 2.1 Letmbe a positive integer, then we have the summation formulas[11]:
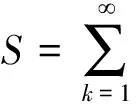
(2.3)
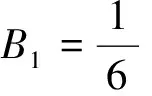
Lemma 2.2 Leta>-1,Re(s)>0,thentheLaplaceintegraltransformofthepowerfunctionxaasfollows[12]:
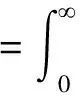
(2.4)
Lemma 2.3 Ifx>1,wehave
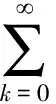
(2.5)
Proof Because
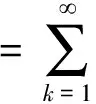
therefore
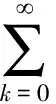
(2.6)
by(2.6),wefind
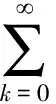
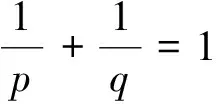
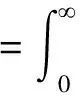
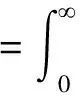
thenwehave
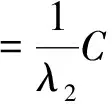
(2.7)
where
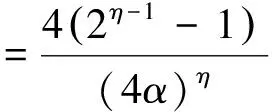
(2.8)
Particularly,whenη=2m(m=1,2,…),Γ(η)=Γ(2m)=(2m-1)!,by(2.3),wefind
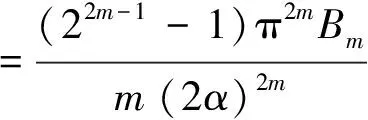
(2.9)
wheretheBm′saretheBernoullinumbers.
Proof Settingαxλ1yλ2=u,thenby(2.4)and(2.6),wehave:
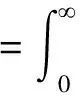
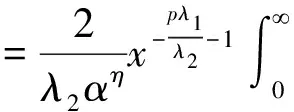


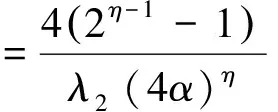

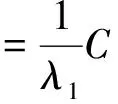
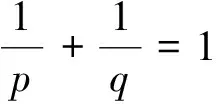
thenwehave:
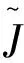
(2.10)

(2.11)
Proof We easily get:
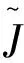
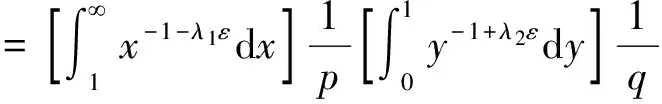

SinceF(u)=uη+1(1-tanhu)iscontinuousin(0,),(u)=0,(u)=0,thereexistsM>0,satisfyingF(u)≤M,byFubini’stheorem[13],wehave:

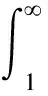
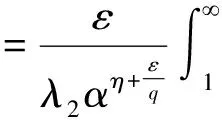
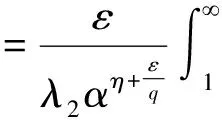
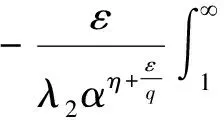
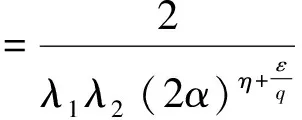
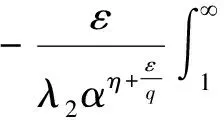
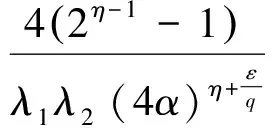


3 Main results and applications
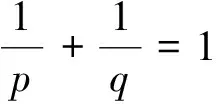

(3.1)
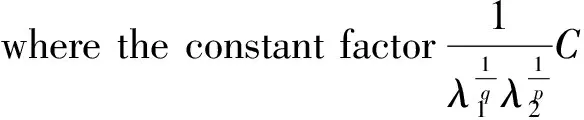
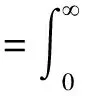
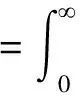
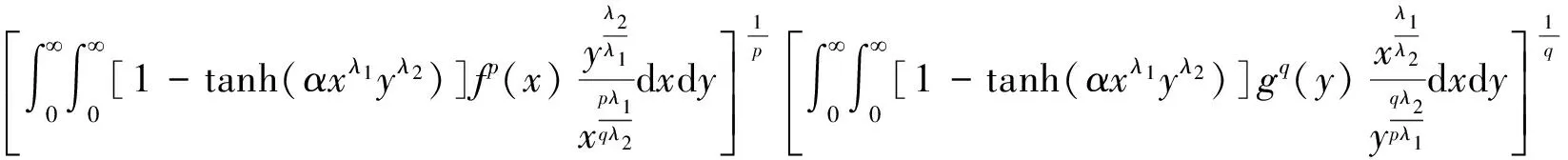
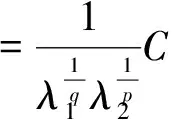
(3.2)
Ifinequality(3.2)keepstheformofanequality,thenaccordingto[14]thereexisttwoconstantsAandB, such that they are not all zero and:
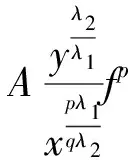

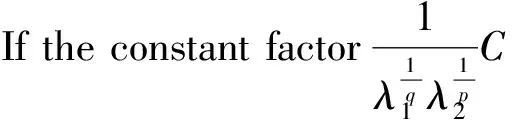
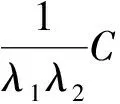
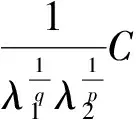
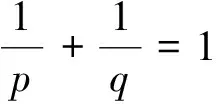

(3.3)
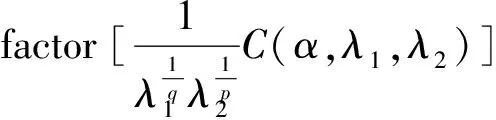
Proof Setting a bounded measurable function as:
since0<‖f‖p,φ<,thereexistsn0∈N, such that 0<φ(x)<(n≥n0),setting:
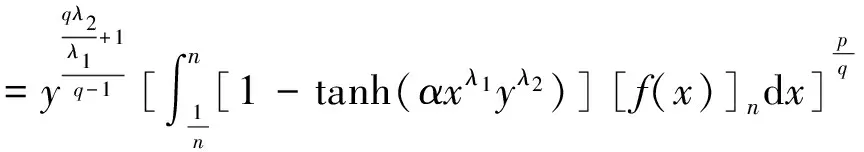
whenn≥n0,by(3.1)wefind:
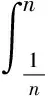
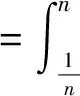

(3.4)
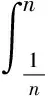
(3.5)
Itfollows0<‖f‖p,φ<.Forn→,by(3.1),both(3.4)and(3.5)stillkeeptheformofstrictinequalities,hence,wehaveinequality(3.3).
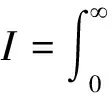
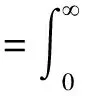
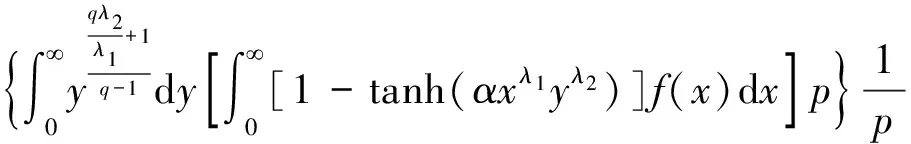
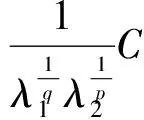
Theinequalityis(3.1),whichisequivalentto(3.3).
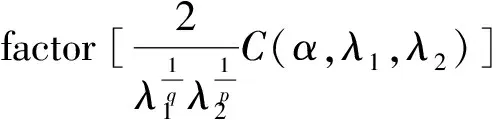
Bytakingthespecialparametervaluesin(3.1)and(3.3),somemeaningfulinequalitiesareobtained:
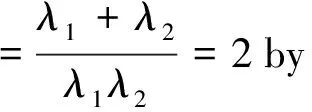

(3.6)
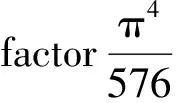
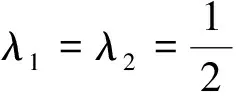

(3.7)

(3.8)
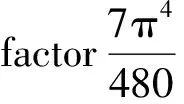
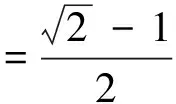

(3.9)

(3.10)
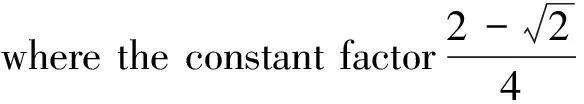
Comments:Veryunfortunately,wecannotgetaHilbert-typeintegralinequalitywiththekernelofthehyperbolictangentfunctionby(3.1).
[1] HARDY G H,LITTLEWOOD J E, PLYA G. Inequalities[M].Cambridge: Cambridge Univ Press, 1952.
[2] HARDY G H. Note on a theorem of Hilbert concerning seris of postive terms[J].Proc London Math Soc, 1925, 23(2):xlv-xlvi.
[3] MINTRINOVIC D S,PECARIC J E,KINK A M. Inequalities involving functions and their integrals and derivertives[M].Boston:Kluwer Academic Publishers,1991.
[4] BICHENG Y. A survey of the study of Hilbert-tpye inequalities with parameters[J].Advances in Mathematics, 2009, 38(3):257-258.
[5] BICHENG Y.On the norm of a Hilbert’s type linear operator and applications[J].J Math Anal Appl,2007,325: 529-541.
[6] JIMENG L, QING L. A generalization of the Hardy-Hilbert’s inequality and its application[J].Acta Mathematics Sinica, Chinese Series, 2009, 52(2): 237-244.
[7] QIONG L, BICHENG Y. A Hilbert-type integral inequality with the mixed kernel of some parameters and its application[J].Journal of Zhejiang University(Science Edition), 2012, 39(2):135-141.
[8] BICHENG Y. On a base Hilbert-type integral inequality and extensions[J].College Mathematics, 2008, 24(2):87-89.
[9] LIU Q, LONG S C. A Hilbert-type integral inequality with the kernel of hyperbolic secant function[J].Journal of Zhejiang University(Science Edition), 2013, 40(3):255-259.
[10] LIU Q, LONG S C. A Hilbert-type integral inequality with the kernel of hyperbolic cosecant function[J].Acta Mathematics Sinica, Chinese Series, 2013, 56(1):97-104.
[11] HUANG Z S,GUO D R. An Intruction to Special Function[M].Beijing:Beijing Press, 2000.
[12] SHU B P,CHEN D L. Complex-variable function and integral transform[M].Beijing:Higher Education Press, 2003.
[13] KUANG J C. Introduction to real analysis[M].Changsha:Hunan Edueation Press,1996.
[14] KUANG J C. Applied inequalities[M].3rd ed.Jinan:Shandong Science and Technology Press,2004.
[15] YANG B C. The norm of operator and Hilbert-type inequalities[M].Beijing:Science press, 2009.
责任编辑:龙顺潮
2015-02-18
国家自然科学基金项目(11171280);湖南省教育厅科学研究项目(10C1186)
黄琳(1964— ),女,江西 上饶人,副教授.E-mail:13787312290@163.com
一个多参数非齐次核Hilbert型积分不等式
黄 琳1*, 刘 琼2
(1.长沙师范学院 初等教育预科部,湖南 长沙 410100;2.邵阳学院 理学与信息科学系,湖南 邵阳 422000)
利用权正数方法和实分析技巧,引入多参数和一些特殊函数联合刻画常数因子,得到一个多参数非齐次核Hilbert型积分不等式和它的等价式,证明了它们的常数因子是最佳的,并讨论了其应用.
Hilbert型积分不等式;权函数;最佳常数因子;非齐次核;多参数
O178
A
1000-5900(2015)03-0001-08

