基于前馈结构的分段时钟同步研究与仿真

张 航，曾安辉

（1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.清华大学，北京 100084）

基于前馈结构的分段时钟同步研究与仿真

张 航1，曾安辉2

（1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.清华大学，北京 100084）

针对数字无线通信系统中全数字接收机的采样时钟同步问题，在利用频域信息估计采样时钟误差的平方率算法的基础上，提出了基于前馈结构的分段时钟同步。通过分段计算数字基带采样信号的频域信息得到采样时钟误差，再通过前馈结构对采样信号进行插值和抽取，实现采样时钟同步。仿真试验表明该算法适用于多径环境和突发通信。

时钟同步；时钟误差估计；立方插值；内插控制

0 引言

在数字无线通信系统中，通过数字信号处理的方法实现采样时钟误差估计及码元符号同步是十分重要的。Gardner提出的无数据辅助时钟误差检测算法在高斯信道环境下具有时钟误差检测范围宽、性能稳定和计算复杂度较低等优点［1］。但Gardner算法收敛时间较长，不适用于短时突发通信系统。文献［2，3］提出了改进的Gardner算法，采用将接收数据先存储后循环处理的策略，解决了Gardner算法收敛时间长的问题，Gardner算法还易受多径干扰的影响。M．Oerder和H．Meyr提出了一种利用频域信息估计时钟误差的平方率算法，该算法假设采样时钟频率偏差很小，可忽略其对时钟同步的影响，利用平方率算法可以估计一段时间内的采样时钟相位偏差［4］。以上传统算法在非高斯信道和突发通信中性能较差。

本文针对以上问题，提出了一种前馈结构的分段时钟同步方法，该算法使用分段估计采样时钟误差的策略，能够在较强多径干扰的条件下较好地跟踪采样时钟频率偏差引起的采样时钟相位变化，抵抗了多径引起的频率选择性畸变；同时该算法处理时延小，可应用于突发通信系统中。

1 系统模型

对于单载波QPSK调制的信号，其发送端的数字基带信号为：

式中，an为发射端码元符号；gT（t）为发送端成形滤波器的响应函数；T为码元符号的周期。

在加性高斯白噪声信道下，接收端数字基带信号为：

式中，an为发射端的码元符号；g（t）为发送和接收成形滤波器的总响应；T为码元符号的周期；N（n）为复加性高斯白噪声；ε为发射机和接收机间的归一化码元符号采样时钟偏差；θ和Δf分别为发射机和接收机间的初始载波相位偏差及载波频率偏差［5］。

本文只关注采样时钟偏差，忽略上下变频本身引起的载波偏差，即在加性高斯白噪声信道下，接收端数字基带信号简化为：

经过周期为Ts的时钟采样后，基带信号表达式为［6］：

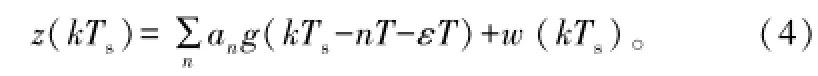
式中，k为整数；z（kTs）为第k个采样时钟周期输出的采样点；εT为由延迟时间τ引起的时间偏移。时钟同步的目的就是从采样点z（kTs）估计出最佳采样点z（nT＋εT）［7－9］。

2 分段时钟同步

2.1 分段时钟同步的结构

本系统采用前馈结构分段采样时钟同步算法来估计和补偿采样时钟误差，前馈结构的采样时钟同步算法的原理框图如图1所示。

图1 前馈结构的采样时钟同步算法

分段时钟同步的主要步骤包括：

①通过时钟误差检测模块分段估计采样时钟误差；

②利用内插控制器将采样时钟误差结果转换成内插参数；

③将过采样数据与内插控制参数输出到内插器，进行插值；

④插值输出最佳采样点，得到码元符号。

2.2 采样时钟误差检测

本系统采用分段处理的办法进行采样时钟同步。利用平方率算法估计每段数据的平均采样时钟相位偏差，然后根据各段估计的采样时钟相位偏差得到插值参数，由内插器进行插值得到最佳码元符号。

设分段数据的时间间隔为LT，若采样时钟Ts＝T／N，其中N≥2，满足奈奎斯特采样定理［10］，则一段数据包含LN个采样点。

利用数据平方残留的采样时钟信息估计得到该段数据的采样时钟偏差为：

式中，

计算c1的详细步骤如下：

①对采样点z（kTs）进行平方运算；

②从第一个点开始计算连续N个数据的一阶傅里叶系数，共得到L个一阶傅里叶系数；

③求L个一阶傅里叶系数的和。

文献［2］给出了基于平方率算法的时钟误差估计算法的方差，表明当分段处理时间间隔LNTs变长时，时钟误差估计的方差越小。

由于相位模糊度的问题，arctan（）函数的输出范围为（－0．5 π，0．5 π），因此时钟误差估计的范围为∈（－0．25，0．25）。

当存在采样时钟频率偏移，设为en，则前后2次时钟误差估计k、k－1的差值就等于时钟频率偏移在LNTs时间内相位的累积，则

由于本算法要求采样时钟频率偏差在各段数据的持续时间LNTs内的相位累积不能超过一个采样点，否则将出现相位跳跃。因此，前后2次时钟误差估计的差值不能超过0．25。得到本系统的采样时钟频率偏移估计范围为：

可以看到，采样时钟频率偏移估计的范围与分段时间长度有关，分段时间越长，则可估计的时钟频率偏移范围越窄。结合前面的时钟误差估计方差与分段时间长度成反比，因此分段时间越长，方差越小，因此估计精度越高。

2.3 插值与内插控制

采样时钟误差检测模块分段计算出采样时钟误差后，需要通过插值模块从过采样数据中得到最佳采样点。内插模块采用非线性立方插值算法，内插模块的数据输入与时钟误差检测模块的输入数据一致，内插控制参数μ由内插控制模块根据采样时钟误差估计得到。内插器模块根据过采样数据和内插控制参数，插值输出最佳采样点。内插模块的立方插值算法采用式（10）所示的插值函数，

式中，内插控制参数μ的范围为（－1，1）；cm（n）为内插系数，表示第n个输入数据在第m阶内插参量。式（10）中的M＝4，N＝2，表示每4个连续数据插值输出一个最佳采样点。内插系数cm（n）的参数设定如表1所示［7］。

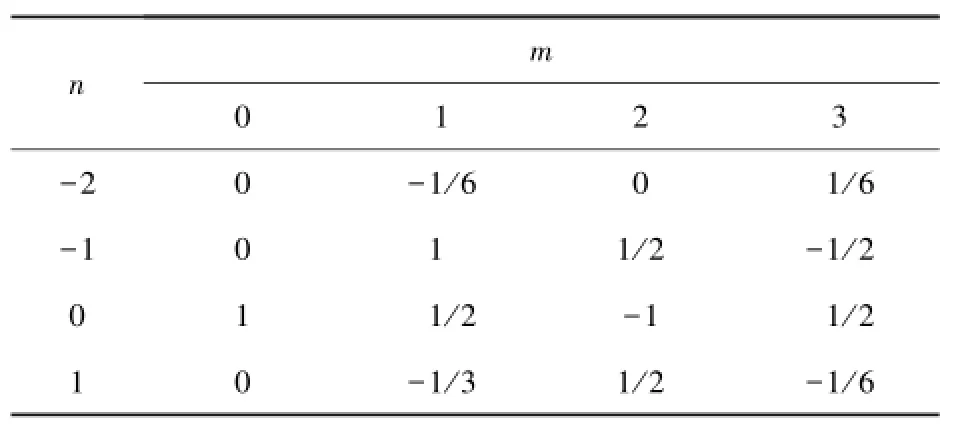
表1 内插器系数

3 仿真结果分析

在高斯信道和多径信道下分别对提出的分段时钟同步算法进行仿真。仿真实验时，数据被分成25段，每段数据的符号数为576个，即式（6）和式（7）中的L＝576。接收端基带信号采用近似4倍符号率对信号进行AD采样。可以算出，本文提出的时钟同步算法理论上的最大采样时钟频率误差范围为±434 PPM。设fs为采样速率，f为符号速率，当fs／f＝4．000 2时，则采样时钟为过采样，时钟偏差为50 PPM。

在高斯信道下，信噪比为20 dB时，测得时钟误差检测算法的时钟频偏捕获范围约为±300 PPM。与理论结果有一定的差异，主要原因为理论计算中时钟误差估计是在无噪声和多径干扰下的结果，而实际仿真时噪声等的影响会带来估计结果的抖动，使估计范围适当缩小。

当采样时钟频率偏差为±300 PPM时，画出每段数据估计的采样时钟误差如图2所示。从图2中可以看出，系统可以跟踪采样时钟偏差引起的相位跳变。

图2 高斯信道下最大和最小采样时钟误差估计曲线

在高斯信道下，采样时钟频率偏差为50 PPM时，对本系统的时钟同步算法的误码率性能进行测试，测得系统的误码率性能如图3所示。从图3中可以看出，在上述条件下，系统的误码率曲线与理论曲线非常接近。

图3 高斯信道下时钟同步算法误码率性能曲线

本时钟同步算法在多径信道下该算法也具有较稳定的性能。假定多径信道模型参数如表2所示，添加高斯白噪声后，信道信噪比为20 dB。

表2 多径信道模型参数

在该多径信道下，系统稳定工作时的采样时钟频偏估计捕获范围约为±200 PPM，时钟误差估计结果如图4所示。

可以看到，在存在较强多径干扰的条件下，本文提出的分段时钟同步算法仍然能够很好地跟踪采样时钟频率偏差引起的采样时钟相位变化，分段时钟同步方法很好地抵抗了多径引起的频域选择性畸变。

图4 多径信道下±200 PPM时钟偏差的估计结果

4 结束语

针对数字通信系统中全数字接收机的采样时钟同步问题，在前人提出的利用频域信息估计采样时钟误差的平方率算法的基础上，提出了前馈结构的分段时钟同步处理方法。本时钟同步方法具有结构简单、处理时延小、不需要额外数据开销且性能稳定等优点，既可用于连续通信也适用于突发通信。

［1］GARDNER，FLOYD M．Interpolation in Digital Modems-Part I：Fundamentals［J］．IEEE Transactions on Communi-cations，1993，41（3）：501－507．

［2］OERDER M，MEYR H．Digital Filter and Square Timing Recovery［J］．Communications，IEEE Transactions on，1988，3（5）：605－612．

［3］姜 龙，张 彧，万晓峰．无线突发通信信道估计及FPGA实现方法［J］．电视技术，2010，34（S1）：94－96．

［4］万晓峰，张 彧，姜 龙．无线突发通信全数字接收机时钟恢复算法［J］．清华大学学报（自然科学版），2010，50（5）：801－804．

［5］张旭东，陆明泉．离散随机信号处理［M］．北京：清华大学出版社，2006．

［6］彭继强，桑会平．采用前馈定时同步的解调器设计与实现［J］．无线电通信技术，2012，38（4）：74－76．

［7］张建志，张丽娜．带通采样时钟沿抖动对解调性能的影响分析［J］．无线电工程，2012，42（10）：10－12．

［8］ERUP L，GARDNER F M，HARRIS R A．Interpolation in Digital Modems Part II：Implementation and Performance［J］．IEEE Transactions on Communications，1993，41（6）：998－1008．

［9］MENGALI U，D’ANDREA A．N．Synchronization Techniques for Digital Receivers［M］．New York：Plenum Press，1997．

［10］樊昌信，曹丽娜．通信原理［M］．北京：国防工业出版社，2006．

Research and Simulation on Feed-forward Segmented Timing Synchronization

ZHANG Hang1，ZENG An-hui2
（1．The 54th Research Institute of CETC，Shijiazhuang Hebei 050081，China；2．Tsinghua University，Beijing 100084，China）

The timing synchronization problem is vital to digital receiver in digital wireless communication system．In this paper，we proposed a feed-forward segmentation timing synchronization method，basing on the frequency information of square sampling data．The synchronization algorithmgets the sampling error by computing the frequency information of digital baseband sampling signalwith segmented method，and completes synchronization using the feed-forward structure with the interpolation and decimation．Simulation re-sults show the method is applicable to the multipath channel and burst communication．

timing synchronization；timing error estimate；cubic interpolation；interpolation control

TN926．2

A

1003－3106（2015）07－0031－04

10．3969／j．issn．1003－3106．2015．07．09

张 航，曾安辉．基于前馈结构的分段时钟同步研究与仿真［J］．无线电工程，2015，45（7）：31－34．

张 航男，（1983—），硕士，工程师。主要研究方向：微波通信技术。

2015-04-06

国家科技重大专项基金资助项目（2014ZX03006－003）。

曾安徽男，（1989—），硕士。主要研究方向：无线突发通信技术。