K－算子值框架的性质

赵茂男，孟 彬

(南京航空航天大学理学院数学系，南京210016)

K－算子值框架的性质

赵茂男，孟 彬

(南京航空航天大学理学院数学系，南京210016)

在算子值框架的基础上，引入了K－算子值框架的概念.通过框架算子，合成算子对K－算子值框架加以刻画.

K－算子值框架;框架算子;合成算子

Hilbert空间中的框架理论最早是由Duffin和Schaeffer［1］在研究非调和Fourier级数时引入的，直至1986年，框架理论才得以关注和深入研究，并且得到了重要研究成果［2－4］.近些年来，框架理论在小波分析、Gabor分析研究中得到迅速发展，在理论上、应用上都起着重要作用，已被广泛应用于信号采样、信号处理、系统模型、图像处理、编码与信号传输等领域.

一般地，对框架的研究都限制在整个空间或者闭子空间上.为了实际应用的方便，最近，Gavruta在研究原子分解系统时引入了更一般的框架，K－框架［5］.孙文昌［6］在Hilbert空间上得到一类推广框架－g－框架，周燕［7，8］在此基础上，推广了g－框架，定义了K－g－框架，探讨了g－框架与K－g－框架的差别，并通过合成算子对K－g－进行刻画.受此启发，本文基于K－框架的上述研究，在Hilbert空间将算子值框架推广，引入K－算子值框架的概念，通过框架算子，合成算子对K－算子值框架加以刻画.

1 预备知识

本文采用如下记号:H，Hj(j∈J指数集)为可分Hilbert空间，B(H，Hj)表示从H到Hj的所有有界线性算子的集合，对每个j∈J，算子Vj∈B(H，Hj).特别地，B(H)表示从H到H的所有有界线性算子的集合.文中非零算子K∈B(H)，K+是K的伪逆算子，K*表示K的伴随算子，Range(K)表示K的值域.

首先介绍复Hilbert空间中的算子值框架和K－算子值框架等的概念.

定义1设H，Hj(j∈J)是Hilbert空间，Vj∈B(H，Hj)，若∃A，B＞0，使得

则称{Vj}j∈J为H上的一个算子值框架.A，B分别称为算子值框架的下界，上界.若(1)中只有右边不等式成立，则称{Vj}j∈J为Bessel算子值序列.如果A=B，则称{Vj}j∈J为紧算子值框架.如果A=B=1，则称{Vj}j∈J为Parseval算子值框架.

类似于标准框架，定义算子值框架{Vj}j∈J的分析算子θV:H→Hj

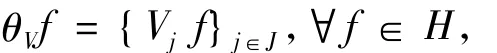
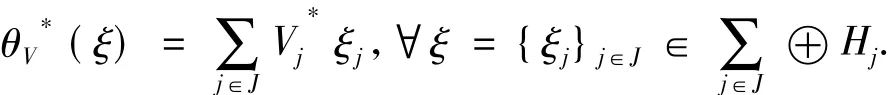
复合θV和，得到算子值框架{Vj}j∈J的框架算子S=θV=Vj.显然{Vj}j∈J是H的算子值框架当且仅当S是有界可逆算子.此外，{}j∈J是H上的Parseval算子值框架.见参考文献［9］.定义2［10］设K∈B(H)，一个序列{fj}j∈J⊂H称为H的K－框架，若∃A，B＞0，使得

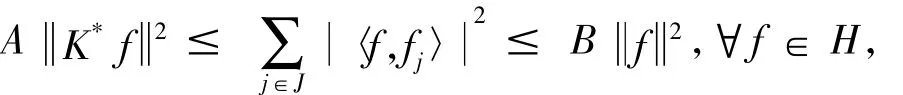
A，B分别称为K－框架的下界，上界.

定义3设H，Hj(j∈J)是Hilbert空间，Vj∈B(H，Hj)，K∈B(H)，若∃A，B＞0，使得

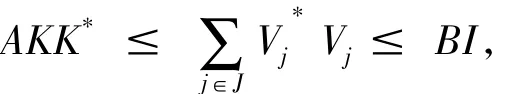
则称{Vj}j∈J为H上的一个K－算子值框架.A，B分别称为K－算子值框架的下界和上界.称有界线性算子S:H→H，Sf=Vjf，∀f∈H为K－算子值框架{Vj}j∈J的框架算子.

注1由K－算子值框架及Bessel序列定义，K－算子值框架必为Bessel序列.

注2若有界线性算子K=I，则K－算子值框架即为定义1中算子值框架.

注3称{Vj}j∈J为H的紧K－算子值框架，若∃A＞0，AKK*=Vj.如果A=1，则称{Vj}j∈J为H的Parseval K－算子值框架.

注4若有界线性算子K=I，则紧K－算子值框架即为紧算子值框架，Parseval K－算子值框架即为Parseval算子值框架.

定义4［11］设Q∈B(H1，H2)，且Q是闭值域的，Q的伪逆Q+唯一存在的条件是:

(1)NQ+=;

(2)RQ+=;

(3)QQ+f=f，∀f∈RQ

注 由(3)知QQ+是空间Range(Q)上的单位算子.

定义5设K∈B(H)，若一个序列{Vj∈B(H，Hj)}j∈J满足

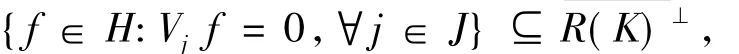
则称序列{Vj}j∈J在H中是－算子值完全的.

引理1［12］设H1、H2为Hilbert空间，B(H1，H2)表示从H1到H2的全体有界线性算子的空间.设L1∈L(H1，H)，L2∈L(H2，H)为两个有界算子，则下面是等价的:

(1)R(L1)⊂R(L2);

(2)L1L1*≤ λ2L2L2*，λ≥0;

(3)∃X∈L(H1，H2)为有界算子，使得L1=L2X.

引理2设{Vj}j∈J为H上界为B的Bessel算子值序列当且仅当可定义合成算子

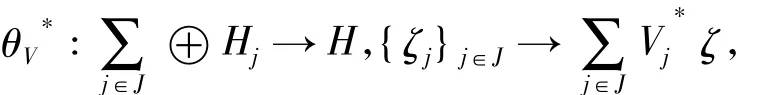
引理3［13］设H，K为Hilbert空间，T:H→K为满的有界线性算子，则算子S=TT*为线性同胚，且=T*(K)，NT*=T(H)⊥={0}，T+=T*S－1.

2 主要结果及结论

K－算子值框架作为算子值框架的一种推广，它具有许多与算子值框架不同的性质.我们知道，算子值框架的框架算子S是自共轭可逆有界线性算子，但K－算子值框架的框架算子不一定自共轭可逆，必须限制在R(K)上.

定理1设K∈B(H)，{Vj}j∈J为H上Bessel算子值序列，可定义有界线性算子:⊕Hj→H，为{Vj}j∈J的合成算子，则下面叙述等价:

(1){Vj}j∈J为H上的K－算子值框架;

定理2假设Vj:H→Hj，{Vj}j∈J为H上的一个K－算子值框架，框架下界，上界分别为A，B，S为其框架算子，且K有闭值域，则(S:R(K)→S(R(K))是可逆有界线性算子.

证明 因为K具有闭值域，则存在伪逆算子，设为K+，∀f∈R(K)，有KK+f=f.则=，故

故∀f∈R(K)，

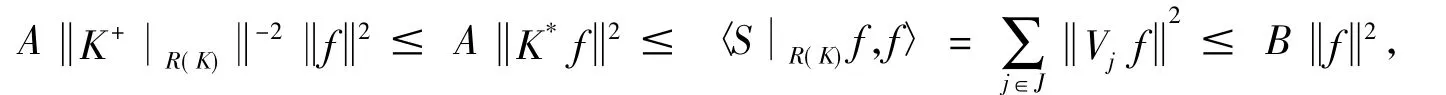
定理3假设Vj:H→Hj，{Vj}j∈J为H上的一个K－算子值框架，框架下界，上界分别为A，B，且K有闭值域，S为其框架算子，且∀f∈R(K)，S(R(K))⊂R(K)，则S:R(K)→S(R(K))是自共轭可逆有界线性算子，并且它的逆算子也是自共轭有界线性算子.

而∀f，g∈R(K)，

下面我们再来探讨K－算子值框架与其合成算子的关系.

定理4设Vj:H→Hj，{Vj}j∈J为H上的一个K－算子值框架，框架下界，上界分别为A，B，其合成算子为，S(R(K))⊂R(K)，其中S为{Vj}j∈J的框架算子.则

(1){Vj}j∈J在H中是R(K)－算子值完全的;

(2)令Q=PR(K)，其中PR(K)表示H→R(K)的正交投影，

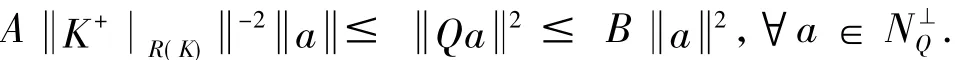
证明(1)由{Vj}j∈J为H上的一个K－算子值框架，框架下界，上界分别为A，B，可得

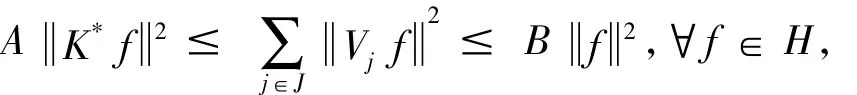
假设f∈{f∈H，Vjf=0}j∈J，则，即K*f=0，由此可得f∈NK*=R(K)⊥，即{f∈H，Vjf=0}j∈J⊂R(K)⊥，故{Vj}j∈J在H中是R(K)－算子值完全的.

(2)令Q=PR(K)θV*，其中PR(K)表示H→R(K)的正交投影，则由引理2可得

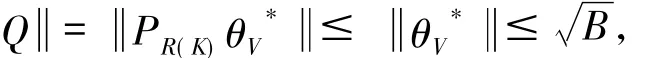
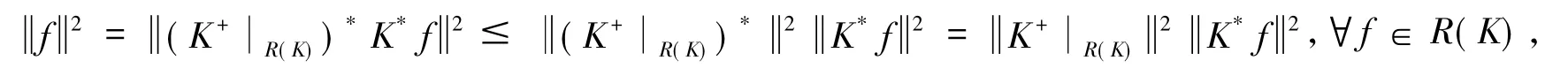
又

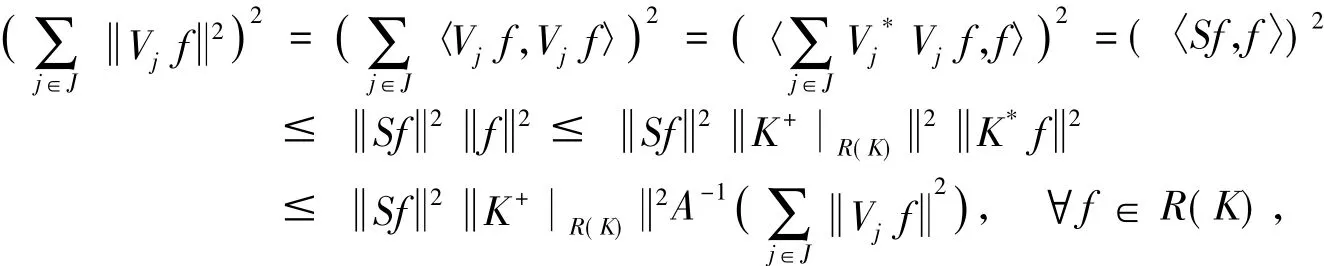
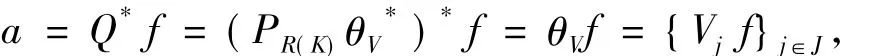
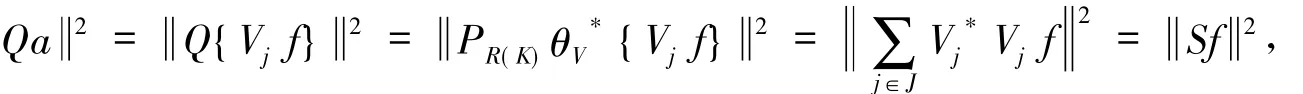
定理5设K∈B(H)且有闭值域，{Vj}j∈J是H上以B为界的Bessel算子值序列为其合成算子，且{Vj}j∈J在H中是R(K)－算子值完全的.∀f∈R(K)Vjf∈R(K).令Q=，满足

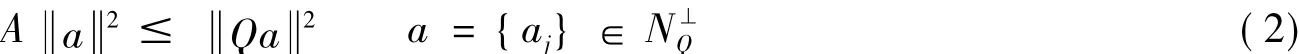
则{Vj}j∈J为H上的K－算子值框架，框架界为A K－2，B.

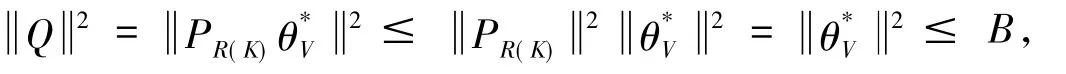
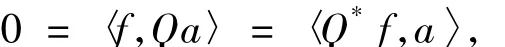
故Q*f=0，则，故VjPR(K)f=0，∀j∈J，又由于{Vj}j∈J在H中是R(K)－算子值完全的，则f∈R(K)⊥，所以

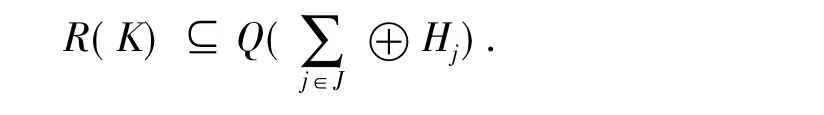
设序列{fn}⊆Q(⊕Hj)=f∈R(K)，则{fn}是R(K)的cauchy列，且存在{xn}⊆⊕Hj使得fn=Q(xn).又由于⊕Hj=⊕NQ，故xn=yn+zn，其中yn∈，zn∈NQ，由(1)得:∀n，m∈N，

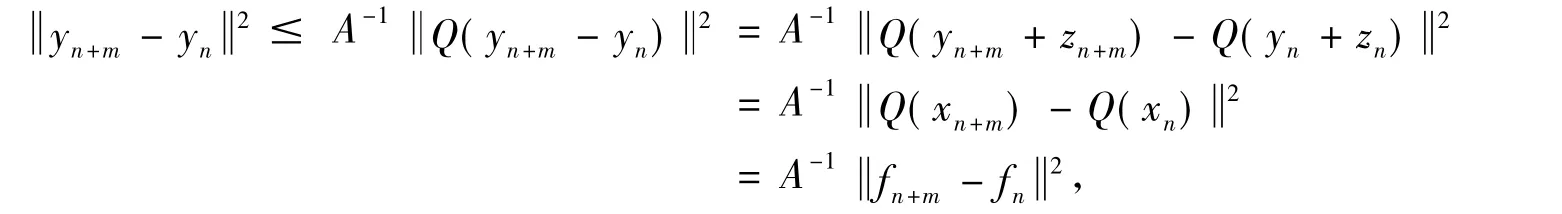
则{yn}是⊕Hj中的cauchy列.又⊕Hj为一个复Hilbert空间，则{yn}收敛于b∈⊕Hj，又由Q的连续性，f=fn=Q(xn)=Q(yn)=Q(b)，故Q(⊕Hj)是R(K)的一个闭子空间.综上，R(K)=Q(⊕Hj).则Q存在伪逆算子Q+，Q+:R(K)→，QQ+f=f，f∈R(K)，则Q+f∈，∀f∈R(K)，由(1)得，

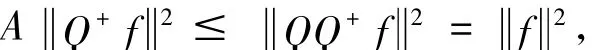
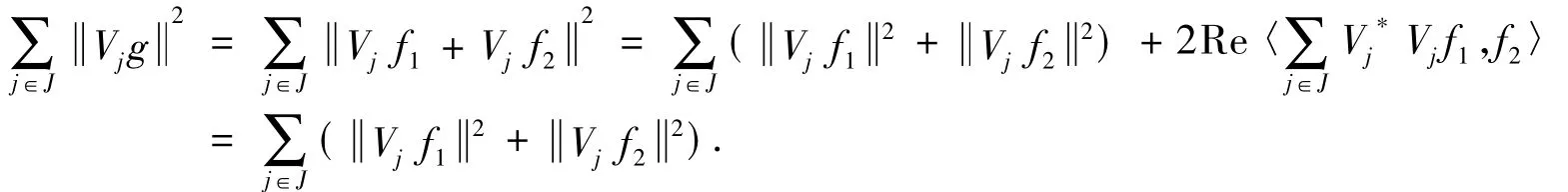
又

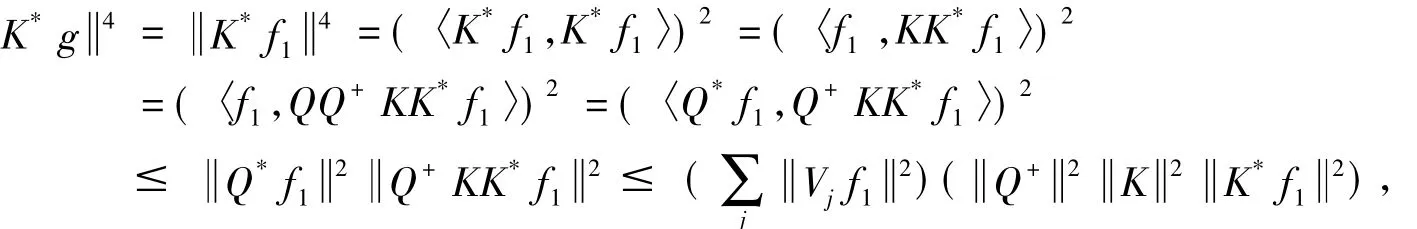
则

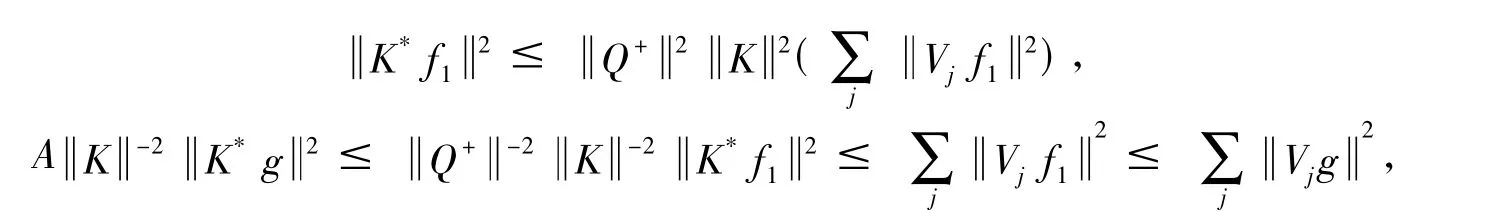
［1］DUFFIN R J，SCHAEFFER A C.A class of nonharmonic Fourier series［J］.Trans Math Soc，1952，72:341－366.

［2］DAUBECHIES I，GROSSMANN A，MEYER Y.Painless nonorthogonal expansions［J］.JMath Phys，1986，27:1271－1283.

［3］CASAZZA PG.The art of frame theory［J］.Taiwannese JMath，2000，4(2):129－201.

［4］CHRISTENSEN O.An introuduction to frames and Riesz bases［M］.Boston:Birkhǎuser，2003.

［5］GǍVRUTA L.Frames for operators［J］.Appl.Comp.Harm.Anan.，2012，32:139－144.

［6］SUNW C.g－frames and g－Riesz bases［J］.J.Math.Anal.Appl.，2006，322(1):437－452.

［7］ 周燕.K－g－框架的刻画［J］.闽江学院学报，2013，34(2):29－32.

［8］ 周燕.K－g－框架与斜对偶［J］.福州大学学报，2014，42(1):25－34.

［9］HAN D，LIP，MENG B，et al.Operator valued frames and structured quantum channels［J］.Science China Mathematics，2011，54:2361－2372.

［10］GAVRUTA P.Frames for operators［J］.Appl Comput Harmon Anal，2012，32:139－144.

［11］Christensen O.An introuduction to frames and Riesz bases［M］.Boston:Birkhǎuser，2003.

［12］DOUGLASR G.Onmajorization，factorization and range inclusion of operators on Hilbert Space［J］.Proc，Amer，Math，Soc，1996，17(2):413－415.

［13］CHRISTENSEN O.Frames and pseudo－inverse［J］.Math Anal Appl，1995，191:401－414.

［责任编辑 王新奇］

Characterizations of K－operator valued frames

ZHAOMao－nan，MENG Bin

(Department of Mathematics，School of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

In this paper，we introduce the definition of K－operator valued frames based on operator valued frames，and then give new characterizations of K－operator valued frames on the properties of their frame operator and synthesis operator.

K－operator valued frames;frame operator;synthesis operator

1008－5564(2015)01－0001－05

O177.2

A

2014－09－20

国家自然科学基金项目(NO.11171151)

赵茂男(1989—)，女，江苏南京人，南京航空航天大学理学院数学系硕士研究生，主要从事泛函分析研究;孟 彬(1976—)，男，山东泰安人，南京航空航天大学理学院副教授，博士，硕士生导师，主要从事泛函分析研究.