Asynchronous H∞Control for Unmanned Aerial Vehicles:Switched Polytopic System Approach
Zhaolei Wang,Qing Wang,and Chaoyang Dong
Asynchronous H∞Control for Unmanned Aerial Vehicles:Switched Polytopic System Approach
Zhaolei Wang,Qing Wang,and Chaoyang Dong
—This study is concerned with theH∞control for the full-envelope unmanned aerial vehicles(UAVs)in the presence of missing measurements and external disturbances.With the dramatic parameter variations in large fl ight envelope and the locally overlapped switching laws in fl ight,the system dynamics is modeled as a locally overlapped switched polytopic system to reduce designing conservatism and solving complexity.Then, considering updating lags of controller′s switching signals and the weighted coef fi cients of the polytopic subsystems induced by missing measurements,an asynchronousH∞control method is proposed such that the system is stable and a desired disturbance attenuation level is satis fi ed.Furthermore,the suf fi cient existing conditions of the desired switched parameter-dependentH∞controller are derived in the form of linear matrix inequality(LMIs)by combining the switched parameter-dependent Lyapunov function method and average dwell time method. Finally,a numerical example based on a highly maneuverable technology(HiMAT)vehicle is given to verify the validity of the proposed method.
IndexTerms—Switchedpolytopicsystem,asynchronous switching,robust control,unmanned aerial vehicles(UAVs),missing measurements.
I.INTRODUCTION
IN recent years,unmanned aerial vehicles(UAVs),such as hypersonic aircraft,highly maneuverable technology (HiMAT)vehicle and agile missile,have received considerable amounts of attention[1-4].The control of UAVs is recognized to be extraordinarily challenging,due to the high nonlinearity and complexity of their motion equations,which stem from the strong couplings between dramatic parameter variations within the full-envelope,wide velocity range and the large unknown environmental disturbances[5-8].
A traditional approach to handle the nonlinearity of fullenvelope UAVs is by means of gain-scheduling[9-10].Its design principle is to design local controllers for each member of a set of operating points that cover the whole fl ight envelope fi rstly and then to obtain a global controller in fl ight by using interpolation method according to the current value of the scheduling parameters[11-12].
However,some poorly developed but important theoretical issues still exist in the gain-scheduled method,such as no guarantees on the robustness,performance,or even nominal stability of the overall gain-scheduled design,especially when the fl ight envelope becomes much wider[13-14].Therefore,it is quite attractive to improve the gain-scheduled method by combining other approach which has appeared in the extant literatures[15-16].
Considering the advantages of switched system theory and the computational complexity of the switched linear parameter-varying(LPV)approach[17-20],an improved gainscheduled controller design approach is proposed in this work based on the switched polytopic systems which have been paid much attention in recent years[21-26].To describe the full-envelope vehicle′s nonlinear model,a locally overlapped switched polytopic system is established evolving on the locally overlapped switching laws which are constructed by considering that the fl ight dynamics can only switch from one region to another adjacent region,where each polytopic subsystem presents the system dynamics in a part of the full fl ight envelope,and its vertices describe the linear dynamics on given characteristic operating points within this part of fl ight envelope.For each polytopic subsystem,a gain-scheduled subcontroller is obtained by interpolating between the controllers on vertices according to the weighted coef fi cients, and the switched parameter-dependent controllers of the fullenvelope are synthesized using these polytopic subsystems′gain-scheduled subcontrollers.
On the other hand,the implicit assumption that the measurements of the system states always contain useful signals is not actually possible[27-31].It can be proved that many measurements consist of noise alone,or involve data missing which can be caused by many practical reasons,such as,measurement failure,intermittent sensor failure,imperfect communication, some of the data being disturbed or coming from a very noisy environment[27].In many engineering applications,such as fl ight control[29-31],due to sensor temporal failure or transmission disturbance at certain time instants,the system measurement may only contain noise,which means the real signal is missing[28].
Moreover,because switching signals and weighted coef ficients of the switched polytopic systems are dependent on the current Mach number and altitude which are measured online in fl ight,missing measurements will lead to the asynchronous switching problem which means there are updating lags between the system mode switching and the controller switching[32-33].To the best of the authors′knowledge,the UAVs′control with missing measurements based on switched polytopic system approach is challenging,and has not been fully investigated yet.
This paper investigates theH∞controller design for UAVswith missing measurements.Firstly,to reduce designing conservatisms and solving complexities,a locally overlapped switched polytopic system is established to describe the fullenvelope fl ight dynamics evolving on the locally overlapped switching laws with the aid of the proposition of a locally overlapped region division method.Secondly,to overcome the effects of the asynchronous switching problems induced by the missing measurements,an asynchronousH∞control method is proposed to guarantee that the system is stable and satis fi es a prescribed attenuation level against the external disturbances. Then,the stability andl2performance analysis is performed by combining the switched parameter-dependent Lyapunov function method and the average dwell time method,and the suf fi cient existing conditions of the switched parameterdependentH∞controller are established in the form of LMIs. Finally,a full-envelope HiMAT fl ight example is given to demonstrate the effectiveness of the proposed approach.
II.MODEL DESCRIPTION
The UAV investigated in this paper is a HiMAT vehicle, a full-envelope and open-loop unstable UAV,which is sponsored by NASA and the U.S.Air Force.It is studied to incorporate technological advances in many fi elds,such as a close-coupled canard con fi guration,aero elastic tailing with composite structures,relaxed static stability,and advanced transonic aerodynamics[34-35].
To derive the linear system model from nonlinear dynamics of the full-envelope vehicle[14-16],Jacobian linearization is performed on the 20 characteristic operating points within the full envelope presented in[34],which are chosen based on the altitudeHand Mach numberMa,as depicted in Fig.1.As each linear model of the chosen operating point can describe the dynamics in its vicinity,the 20 models can cover the nonlinear dynamic behaviors of the HiMAT vehicle within the full envelope[34].

Fig.1.Flight envelope and the operating points.
Considering that the longitudinal motion stability and maneuverability primarily depend on the short period motion, with the aid of 20 continuous-time longitudinal linear models in[34],the longitudinal short period model of thei-th operating point can be modeled as the discrete time model(1)by setting the system′s sampling period to beT,which is

Here,xxx=(α,q)Tis the state vector,andα,qdenote angle of attack,pitch rate,respectively.uuu=(ξe,ξv,ξc)Tis the control input,ξe,ξv,ξcdenote elevator,elevon and canard de fl ection,respectively.yyyis the output,andddd∈L2[0,∞)is the unknown external disturbances.The real system matricesAi,Bi,Ci,Bd,i,Dd,ifor thei-th characteristic operating point,i∈Ω={1,2,···,20},are of appropriate dimensions with the index set Ω denoting the collection of all characteristic operating points within the envelope,and the trim condition for every operating point is illustrated in Table I.

TABLE I THE 20 OPERATING POINTS OF HIMAT VEHICLE
To reduce designing conservatisms and solving complexities,the large-scale fl ight envelope shown in Fig.1 is divided intoNregions referring to the switched LPV approach.The index set Ω is accordingly divided intoNindex subsets which are de fi ned as Ω1,Ω2,···,ΩNto represent the collection of the characteristic operating points within each region.
In our work,a polytopic system is adopted to represent the system dynamics in each region,and its vertices are those characteristic operating points within this region.Inspired by the gain-scheduled method,the system dynamics of current operating point within this region is obtained by interpolating among the system dynamics on vertices.
Considering the fl ight dynamics can only switch from the current region to another adjacent region in the full-envelope fl ight,a locally overlapped switched polytopic system is furthermore established as follows:

wherek∈N is time instant,and the switching lawsσ(k)∈Γ stands for variation of the fl ight region according tok,where the set Γ={1,2,···,N}is the collection of the fl ight region indices,withNbeing a fi nite integer denoting the number of fl ight regions.The system matrices of(2)satisfy that

Considering the locally overlapped property ofσ(k)within the full-envelope fl ight,the fl ight regions must be divided under the following conditions:
Condition 1.Sm∈ΓΩm=Ω.
Condition 2.Ωσ(k)∩Ωσ(k+1)N.
Taking the fl ight trajectory depicted in Fig.1 for example, the fl ight envelope can be partitioned into three fl ight regions, and one has

Remark 1.Condition 1 guarantees the index subsets must involve all the characteristic operating points within the fl ight envelope.Condition 2 guarantees the switching occurs between two adjacent regions that share common characteristic operating points.Thus,the switching on the boundary of two adjacent regions will not induce non-smooth change of the weighted coef fi cientaaak,providedaaakis only calculated by using these common vertices of the adjacent polytopic subsystems.For example,the controller gains on the boundary of the Region 1 and Region 2 are only interpolated by the gains on characteristic operating Points 6 and 7.
III.PROBLEM FORMULATION
In this section,a switched parameter-dependent state feedbackH∞controller is designed to guarantee that the system is stable and satis fi es a prescribed performance level.Firstly, the following assumptions are made.
Assumption 1.System statexxxis measurable,and the missing measurements ofxxxare described by a Bernoulli distributed stochastic variableθ(k)∈{0,1},where Pr{θ(k)= 1}=ρ,Pr{θ(k)=0}=1-ρ.θ(k)=1 stands for the normal case,whileθ(k)=0 stands for the missing measurement case, accordingly[27].
Thus,the state feedback controller′s inputzz z(k)is given by

With the locally overlapped switching laws∀σ(k)∈Γ, the discrete state feedback switched parameter-dependent controller(6)is designed as

where subcontrollerKm(aaak),∀σ(k)=m∈Γ of polytopic subsystemmis synthesized as follows:
whereKiis the controller gain to be determined for thei-th characteristic operating point.
Remark 2.Because the partition information of the fl ight regions is stored in controller unit previously,σ(k)can be determined online by judging which region the current Mach number and altitude belong to,andaaakcould also be calculated referring to the fi nite element theory[23].
Remark 3.Considering the measured Mach number and altitude data will be missing at some instants,there will be updating lags forσ(k)andaaak,which will further induce asynchronous switching phenomena between the system modes and controllers.Moreover,the asynchronous switching here will be more complex than that in[32-33],because neitherσ(k)noraaakcan be obtained in time.
Due to the asynchronous switching,the Lyapunov function value may moderately increase even during the active time of certain subsystems except at the switching instants,but the increase rate must be bounded[32].For concise notation,letkvandkv+1,v∈N denote the starting time and ending time of some active subsystem,whileT↑(kv,kv+1)andT↓(kv,kv+1) represent the unions value of the dispersed intervals during which Lyapunov function is increasing and decreasing within the interval,whereT↓(kv+1-kv)andT↑(kv+1-kv)denote the length ofT↑(kv,kv+1)andT↓(kv,kv+1),respectively[33].
As a result of the updating lags ofσ(k),the Lyapunov function value of the polytopic subsystem may moderately increase,and the correspondingT↑(kv,kv+1)will be only the interval close to the switching instants.AsT↑(kv+1-kv) may vary at different instants,without loss of generality,the maximal lag of the Mach number and altitude data is assumed to beδmT,whereδmis known a priori here[33].
Thus,the controller in(6)will be transformed to(8)under the asynchronous switching,i.e.,

Then,theH∞controller design for the HiMAT vehicle with missing measurements is summarized as follows.Considering the locally overlapped switched polytopic system(2)with missing measurements described in(5),for a positive constantγ,determine the matricesKi(i∈Ω)of asynchronous controller in(8),such that system(9)is stable and has a weightedl2-gain performance(10)under zero initial conditions,that is,

where 0<λ<1,andγ>0.
Remark 4.In the presence of missing measurements and the locally overlapped switching laws,a Bernoulli distributed stochastic variable is introduced to describe the missing measurements,and an augmented locally overlapped switching polytopic stochastic system(9)is further established.Obviously,the asynchronousH∞control problem for(9)in our work is more complicated than the existentH∞control problem for the switched polytopic system.
IV.MAIN RESULTS
In this section,the suf fi cient existing conditions of the desired controller will be derived in the form of LMIs.Firstly, we present the following de fi nition and lemmas on the stability andl2-gain analysis here for later use.
De fi nition 1[32].For switching signalσ(·)and anyk≥1, letNσ[0,k)be the switching numbers ofσ(·)over the interval [0,k).If for any givenN0≥0 andτa>0,we haveNσ[0,k)≤N0+k/τa,thenτaandN0are called average dwell time and the chatter bound,respectively.Without loss of generality,we chooseN0=0 for convenience as commonly used in the literature.
Lemma 1.Consider system(9),and let 0<λ<1,β≥0 andµ≥1 be given constants.Suppose that there existC1functionsVσ(k),σ(k)=m∈Γ,and two classκ∞functionsκ1,κ2such that
Thus,the system is globally uniformly asymptotically stable in the mean(GUAS-M)for any switching signal with average dwell timeτasatisfying
Proof.Referring to the method in[33],∀k∈[kv,kv+1),it holds from(12)that
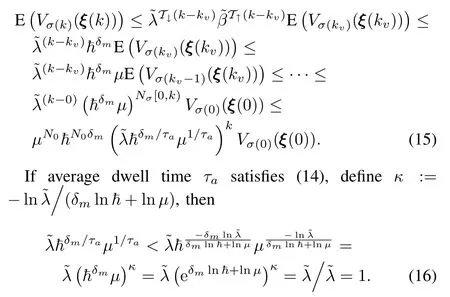
Therefore,we can get that E¡Vσ(k)(ξ(k))¢→0 ask→∞, and system(9)is GUAS-M with the aid of(11)by using the same method as in[36].□
Lemma 2.Consider system(9),and let 0<λ<1,β≥0,µ≥1 andγm>0(∀m∈Γ)be given constants.Suppose that there existC1functionsVσ(k),σ(k)=m∈Γ,such that (13)is satis fi ed and

A.Stability and l2-Gain Performance Analysis

Then system(9)is GUAS-M whenddd(k)=0 for any switching signal with average dwell timeτasatisfying

and has the weightedl2-gain performance index(10)under zero initial conditions,whereγ=max{γm},∀m∈Γ,= 1-λ,and=1+β.
Proof.Firstly,we choose the following Lyapunov-like function(21)based on the switched parameter-dependent Lyapunov function method[38]:

From Remark 1,it is clear that switchings on the boundary of two adjacent regions will not induce non-smooth change of the weighted coef fi cientaaak,becauseaaakis calculated by using only these common vertices of the adjacent polytopic subsystems.So,when the switching occurs,we have



Thus,we getµ=1 at the switching instant from(13),and it can be derived from(14)that the dwell timeτaof system (9)must satisfy(20).
Secondly,we prove the stability of system(9).To this end,assume thatdd d(k)=0.For any non-zeroξ(k),∀k∈[kv+δm,kv+1),and any switching signalσ(k)=m∈Γ, one has(23)holds.
Similarly,for any non-zeroξ(k),∀k∈[kv,kv+δm),and any switching signal'σ(k)==n“∈Γ×Γ,Ωm∩Ωn/,one has(24)holds.
AsPi≥0,i∈Ωm,∀m∈Γ,(25)and(26)will be obtained by perfo'rming a congruenc“e transformation to(18)and(19) by diagand the Schur complement.
Noticing the(1,1)block of Θi,j,landcan imply
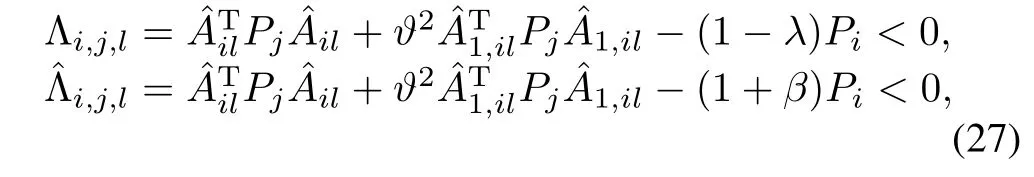
we can have[38]
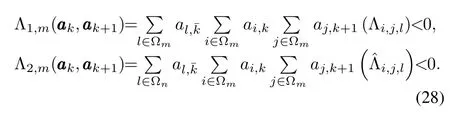
Clearly,(29)holds according to(23),(24)and(28).
Thus,we can get

Combining(20),(33)and Lemma 2,it can be derived that system(9)is GUAS-M for any switching signal with average dell time(20).As a result ofµ=1 andN0=0,the weightedl2-gain performance index in(10)is degraded to beγ=max{γm},∀m∈Γ.□
B.H∞Controller Design
Based on Theorem 1,the suf fi cient existing conditions of the state feedbackH∞controller in(8)are derived.

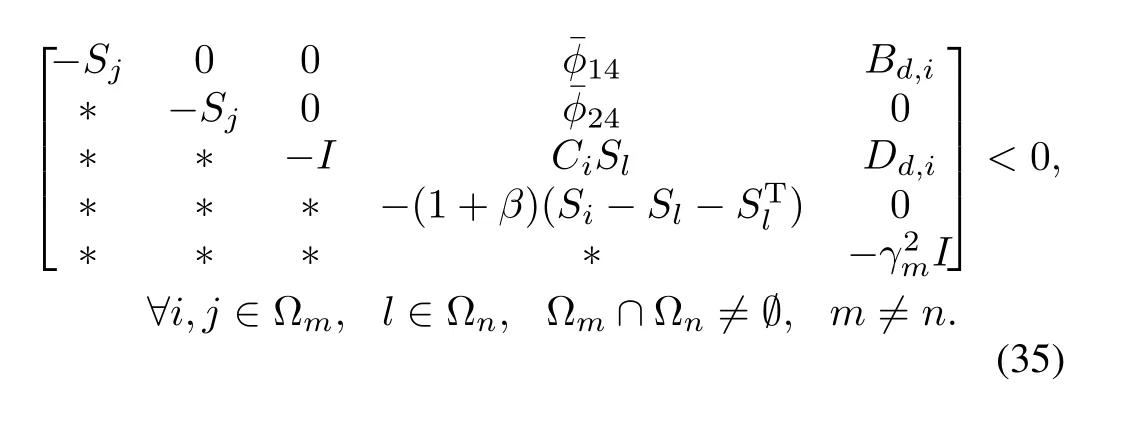
Then under the asynchronous delayδm,system(9)is GUASM for any switching signals withτasatisfying(20),and has a weightedl2-gain performance indexγ=max{γm},∀m∈Γ. Moreover,if a feasible solution exists,the desired controller gains in(8)are given by
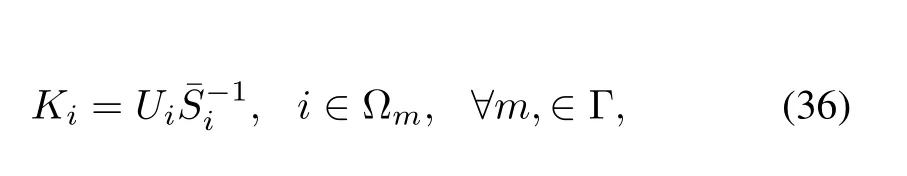

Meanwhile,the switched parameter-dependent controller gains are given by(36)according to the de fi nition thatUi:=Ωm,∀m∈Γ.□
Remark 5.Referring to Theorem 2,a similar conclusion can be obtained for the input-to-state stability of the homologous systems which have reference inputs.This corollary can be directly obtained from Lemma 1 in[18]which will be validated later in the numerical example section.
V.NUMERICAL EXAMPLE
In this section,a numerical example is provided to illustrate the effectiveness of the proposed method.
Suppose that the sampling period isT=0.025s,then corresponding system matricesAi,Biin(1)can be obtained with the aid of the continuous-time system matrix parameters in[34].Moreover,other system matrices are given below, wherei∈Ωm,∀m∈Γ:

The external disturbancedddis supposed to be a random sequence uniformly distributed over[-0.1,0.1].Moreover,it is assumed that E{θ(k)}=ρ=0.95,which means that the probability of the measured system statexxxbeing successfully transmitted to the controller is 0.95,and Fig.2 shows the actual response ofθ(k).

Fig.2.Missing measurement modeθ(k).
The performance of the proposed switched parameterdependent controller for the full-envelope HiMAT vehicle is validated by a large-scale fl ight trajectory,i.e.,2-4-5-7-8-9-12-14-15-17,which is depicted in Fig.1.The variation of altitude and Mach number are depicted in Fig.3.

Fig.3.Variation of the altitude and Mach number.
The fl ight envelope can be partitioned into three regions which are given in(4),and the fl ight trajectory includes two switchings between the three polytopic subsystems.First switching occurs when the HiMAT vehicle enters characteristic operating Point 7,and the second switching occurs when the HiMAT vehicle enters characteristic operating Point 12 which can give the fact that the average dwell timeτa=1600(40s) from De fi nition 1.Supposed that the maximal lagδm=5, it can be calculated thatτ∗a=5(0.1250s)which implies the constraint condition in(20)can be easily satis fi ed.
To analyze the input-to-state stability[18],the controller in (6)is modi fi ed into the following form:
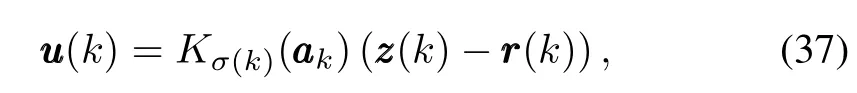
whererrr(k)=[αcqc]Tis the command input,including angle of attack command and pitch rate command.By settingγmas the optimization variable at the same time,the YALMIP toolbox in Matlab is used to solve the optimization problem in Theorem 2,whereλ=0.01 andβ=0.01 are given. Then,we can getγ∗=1.9237,and the controller gains can be obtained,which are shown as follows:

The controller gains for the characteristic operating points are given above,so the gain-scheduled subcontroller for each polytopic subsystem is interpolated by(7).In this work,the gain-scheduled subcontrollers are interpolated in triangular regions,namely,three characteristic operating points,which are the closest to the current one,are chosen.
For example,for the triangular regions which are constructed by the characteristic operating Points 2,4 and 5 in Region 1,the gain-scheduled subcontroller is interpolated by three gainsK2,K4andK5.Given the fl ight condition in this fl ight region with altitude and Mach number(ha,Ma)at instantk,then the interpolated gain-scheduled subcontroller gain can be calculated as

and the weighted coef fi cientaaaksatis fi es
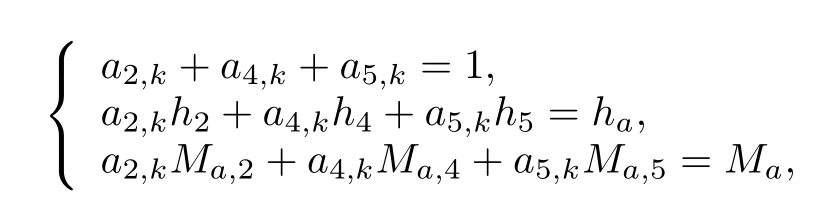
wherehi,Ma,i,i∈Ω are altitude and Mach number for thei-th characteristic operating point.
Fig.4 demonstrates the response of angle of attack,and pitch rate is shown in Fig.5 where the pitch rate command is set to be zero.We can conclude from Figs.4 and 5 that the tracking performance of angle of attack is acceptable in the full fl ight envelope,and the pitch rate response is satisfying.

Fig.4.Angle of attack response.
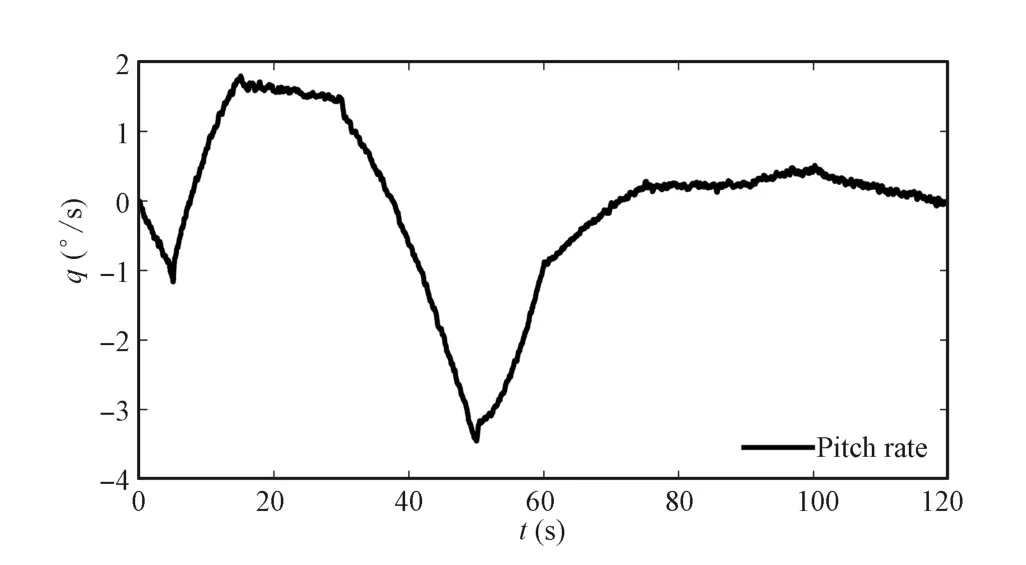
Fig.5.Pitch rate response.
The control surface de fl ections are shown in Figs.6~8, which are achievable and practical.
From the simulation results above,it can be concluded that the HiMAT vehicle is stable in the full-envelope fl ight with robustness against the external disturbances,and can also restrain the effect of asynchronous switching to guarantee a desired performance.

Fig.6.Elevator de fl ection.

Fig.7.Elevon de fl ection.

Fig.8.Canard de fl ection.
VI.CONCLUSION
This study proposed an improved gain-scheduled controller design approach for the full-envelope UAVs with missing measurements and external disturbances.A locally overlapped switched polytopic system is established to describe fl ight dynamics within full fl ight envelope,and an asynchronous robustH∞synthesis approach is utilized to obtain a prescribed disturbance attenuation level.The proposed approach could also be expanded to other applications where the locally overlapped switched polytopic system model could be established, and the missing measurements and asynchronous switching phenomena exist.Future works will analyze the impact of system states that cannot be measured,and the output feedback control problem will be concerned.
REFERENCES
[1]Dierks T,Jagannathan S.Output feedback control of a quadrotor UAV using neural networks.IEEE Transactions on Neural Networks,2010, 21(1):50-66
[2]Beard R W,McLain T W,Goodrich M A,Anderson,E P.Coordinated target assignment and intercept for unmanned air vehicles.IEEE Transactions on Robotics and Automation,2002,18(6):911-922
[3]He Y Q,Han J D.Acceleration feedback enhancedH∞disturbance attenuation control for a class of nonlinear underactuated vehicle systems.Acta Automatica Sinica,2008,34(5):558-564
[4]Azinheira J R,Moutinho A.Hover control of an UAV with backstepping design including input saturations.IEEE Transactions on Control Systems Technology,2008,16(3):517-526
[5]Sieberling S,Chu Q P,Mulder J A.Robust fl ight control using incremental nonlinear dynamic inversion and angular acceleration prediction.Journal of Guidance,Control,and Dynamics,2010,33(4):1732-1742
[6]Yang K,Shin J,Sukkarieh S.Integrated planning and control of rotary-wing unmanned aerial vehicle navigation.Journal of Aerospace Computing,Information,and Communication,2012,9(3):81-91
[7]Hu X X,Wu L G,Hu C H,Gao H J.Adaptive sliding mode tracking control for a fl exible air-breathing hypersonic vehicle.Journal of the Franklin Institute,2012,349(2):559-577
[8]Orqueda O A A,Zhang X T,Fierro R.An output feedback nonlinear decentralized controller for unmanned vehicle coordination.International Journal of Robust and Nonlinear Control,2007,17(9):1106-1128
[9]Rugh W J,Shamma J S.Research on gain scheduling.Automatica,2000, 36(7):1401-1425
[10]Leith D J,Leithead W E.Survey of gain-scheduling analysis and design.International Journal of Control,2000,73(8):1001-1025
[11]Ginter V J,Pieper J K.Robust gain scheduled control of a hydrokinetic turbine.IEEE Transactions on Control Systems Technology,2011,19(4): 805-817
[12]Saussi´e D,Saydy L,Akhrif O,B´erard C.Gain scheduling with guardian maps for longitudinal fl ight control.Journal of Guidance,Control,and Dynamics,2011,34(4):1045-1059
[13]Huang Y Q,Sun C Y,Qian C S,Zhang J M,Wang L.Polytopic LPV modeling and gain-scheduled switching control for a fl exible air-breathing hypersonic vehicle.Journal of Systems Engineering and Electronics,2013,24(1):118-127
[14]Sunan C.Robust Gain-scheduledH∞Control for Unmanned Aerial Vehicles[Ph.D.dissertation],Cran fi eld University,England,2010.
[15]Natesan K,Gu D W,Postlethwaite I.Design of staticH∞linear parameter varying controllers for unmanned aircraft.Journal of Guidance, Control,and Dynamics,2007,30(4):1829-1835
[16]Huang Y Q,Sun C Y,Qian C S,Wang L.Non-fragile switching tracking control for a fl exible air-breathing hypersonic vehicle based on polytopic LPV model.Chinese Journal of Aeronautics,2013,26(2):948-959
[17]Lu Q,Zhang L,Shi P,Karimi H R.Control design for a hypersonic aircraft using a switched linear parameter-varying system approach.Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2013,227(1):85-95
[18]Hespanha J P,Morse A S.Stability of switched systems with average dwell-Time.In:Proceedings of the 38th Conference on Decision and Control.New York,USA:IEEE,1999.2655-2660
[19]Hou Y Z,Dong C Y,Wang Q.Stability analysis of switched linear systems with locally overlapped switching law.Journal of Guidance, Control,and Dynamics,2010,33(2):396-403
[20]Zhao X,Zhang L,Shi P,Liu M.Stability of switched positive linear systems with average dwell time switching.Automatica,2012,48(4): 1132-1137
[21]Zhang L,Wang C,Chen L.Stability and stabilization of a class of multimode linear discrete-time systems with polytopic uncertainties.IEEE Transactions on Industrial Electronics,2009,56(9):3684-3692
[22]Wang R,Shi P,Wu Z G,Sun Y T.Stabilization of switched delay systems with polytopic uncertainties under asynchronous switching.Journal of the Franklin Institute,2013,350(8):2028-2043
[23]Hou Y,Wang Q,Dong C.Gain scheduled control:switched polytopic system approach.Journal of Guidance,Control,and Dynamics,2011, 34(2):623-629
[24]Wang H,Ju H H,Yang G H.Fault detection fi lter design for linear polytopic uncertain continuous-time systems.Acta Automatica Sinica, 2010,36(5):742-750
[25]Xiang W M,Xiao J.H∞controller design for a class of switched linear discrete-time system with polytopic uncertainties.Proceedings of the Institution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2012,226(7):1311-1322
[26]Zhang L X,Shi P,Boukas E K,Wang C H.H∞control of switched linear discrete-time systems with polytopic uncertainties.Optimal Control Applications and Methods,2006,27(3):273-291
[27]Gao H,Chen T,Wang L.Robust fault detection with missing measurements.International Journal of Control,2008,81(3):804-819
[28]Wang Z D,Shen B,Liu X H.H∞fi ltering with randomly occurring sensor saturations and missing measurements.Automatica,2012,48(3): 556-562
[29]Long Y,Yang G H.Fault detection in fi nite frequency domain for networked control systems with missing measurements.Journal of the Franklin Institute,2013,350(9):2605-2626
[30]Liu F Q,Huang J,Shi Y,Xu D M.Fault detection for discretetime systems with randomly occurring nonlinearity and data missing: a quadrotor vehicle example.Journal of the Franklin Institute,2013, 350(9):2474-2493
[31]Xu L,Wang Q,Li W,Hou Y.Stability analysis and stabilisation of fullenvelope networked fl ight control systems:switched system approach.IET Control Theory Applications,2012,6(2):286-296
[32]Zhang L X,Gao H J.Asynchronously switched control of switched linear systems with average dwell time.Automatica,2010,46(3): 953-958
[33]Zhang L X,Shi P.Stability,l2-gain and asynchronousH∞control of discrete-time switched systems with average dwell time.IEEE Transactions on Automatic Control,2009,54(9):2193-2200
[34]Hartmann G L,Barrett M F,Greene C S.Control Design for an Unstable Vehicle,Technical Report CR-170393,NASA,USA,1979.
[35]Safonov M G,Laub A J,Hartmann G L.Feedback properties of multivariable systems:the role and use of the return difference matrix.IEEE Transactions on Automatic Control,1981,26(1):47-65
[36]Zhang L,Boukas E K,Shi P.ExponentialH∞fi ltering for uncertain discrete-time switched linear systems with average dwell time:aµ-dependent approach.International Journal of Robust and Nonlinear Control,2008,18(11):1188-1207
[37]ChatterJee D,Liberzon D.Stability analysis of deterministic and stochastic switched systems via a comparison principle and multiple Lyapunov functions.SIAM Journal on Control and Optimization,2006, 45(1):174-206
[38]Daafouz J,Bernussou J.Parameter dependent Lyapunov functions for discrete time systems with time varying parametric uncertainties.Systems and Control Letters,2001,43(3):355-359


Qing Wang received her master and Ph.D.degrees in fl ight vehicle control guidance and simulation from Northwestern Polytechnical University, in 1993 and 1996,respectively.She worked as a post-doctoral researcher in the Department of Automatic Control,Beijing University of Aeronautics and Astronautics from 1996 to 1998.She worked in China Academy of Space Technology in 1999,and visited Moscow College of Aeronautics as a visitor during this period.She is now a professor in the Department of Guidance,Navigation and Control at the School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics.Her research interests include guidance and control of aerospace vehicles,intelligent fl ight control system.

Chaoyang Dong received his master degree from Northwestern Polytechnical University in 1992,and Ph.D.degree in guidance,navigation and control from Beijing University of Aeronautics and Astronautics.From 2002 to 2008,he was an associate professor in the Department of Automatic Control, Beijing University of Aeronautics and Astronautics. He is now a professor of fl ight mechanics at the School of Aeronautic Science and Engineering,Beijing University of Aeronautics and Astronautics.His research interests include kinetic analysis of fl exible vehicle and control of the complex dynamics system.
ang
his bachelor degree from Beijing Institute of Technology,Beijing,China in 2009.He received his Ph.D.degree in navigation guidance and control from School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing,China, in 2015.He is an engineer of Beijing Aerospace Automatic Control Institute,Beijing,China.His research interests include networked control system, fault diagnosis,switched system theory and its application on fl ight vehicle.Corresponding author of this paper.
Manuscript received October 10,2013;accepted May 15,2014.This work was supported by National Natural Science Foundation of China(61273083, 61074027).Recommended by Associate Editor Bin Xian.
:Zhaolei Wang,Qing Wang,Chaoyang Dong.AsynchronousH∞control for unmanned aerial vehicles:switched polytopic system approach.IEEE/CAA Journal of Automatica Sinica,2015,2(2):207-216
Zhaolei Wang is with the School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China,and also with Beijing Aerospace Automatic Control Institute, Beijing 100854,China(e-mail:beiliwzl123@163.com).
Qing Wang is with the School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China(e-mail:wangqing@buaa.edu.cn).
Chaoyang Dong is with the School of Aeronautical Science and Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191, China(e-mail:dongchaoyang@buaa.edu.cn).
 IEEE/CAA Journal of Automatica Sinica2015年2期
IEEE/CAA Journal of Automatica Sinica2015年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Single Image Fog Removal Based on Local Extrema
- An Overview of Research in Distributed Attitude Coordination Control
- Operation Ef fi ciency Optimisation Modelling and Application of Model Predictive Control
- Cloud Control Systems
- Stable Estimation of Horizontal Velocity for Planetary Lander with Motion Constraints
- Production Line Capacity Planning Concerning Uncertain Demands for a Class of Manufacturing Systems with Multiple Products
