基于ARX 模型的局部阴影光伏阵列非机理建模研究

牛拴保， 霍 超， 程 林， 孙黎霞， 李兆伟，崔晓丹

（1. 国家电网公司西北分部 陕西 西安 710048； 2. 河海大学 能源与电气学院， 江苏 南京 211100；3. 南京南瑞集团公司 江苏 南京 211100）

近年来， 大规模的光伏发电系统对电力系统产生了巨大影响。 而光伏阵列的建模是光伏发电系统的基础，其输出特性直接影响系统的整体效果。 所以，建立能够准确描述光伏系统输出特性的模型是进行相关研究与仿真的基础，具有重要意义。

均匀光照下，工程用四参数模型在实际应用与仿真研究方面均具有很高的精度。 而在局部阴影情况下，阴影的存在使得光伏阵列的P-V 特性曲线与典型光伏电池的P-V 特性曲线存在很大不同，传统光伏电池的等效模型已不再适用[1]。针对这一问题，文献[2]建立了阴影条件下光伏阵列的数学模型， 深入研究了阴影情况下光伏阵列的输出特性与阴影数量、光照、温度、遮挡模式等因素之间的关系；文献[3]应用并联旁路二极管的建模方法以避免阴影下电池的损坏；文献[4]提出基于支持向量机的局部阴影条件光伏阵列建模策略；文献[5]提出以电流方程分段函数进行建模；文献[6]介绍了以电压分段函数进行建模的方法。 上述方法建立的光伏组件机理模型能够适用于局部阴影光伏阵列的仿真研究，但是模型较为复杂且非线性很强。

基于上述分析，为避免考虑复杂的机理模型，本文提出基于ARX 模型的阴影光伏阵列非机理模型。 首先，从改进的阴影光伏阵列机理模型中仿真获得输出电压、电流和功率数据，再对局域峰值之前的I-V 曲线段所采集的数据进行预处理，即按照精度要求进行线性插值，将预处理后的数据作为系统辨识的数据输入。 然后，在MATLAB 系统辨识工具箱的模型类型中选择常用的ARX 模型，通过改变ARX 模型的阶次获得不同的辨识模型。 最后，选择精确度最高的辨识模型作为所需要的阴影光伏阵列非机理模型输出。

1 局部阴影光伏阵列机理模型改进

准确获得输入数据是进行离线辨识的前提。 所以，对于阴影光伏阵列模型的辨识而言，正确建立输出数据的阵列机理模型十分重要。 根据文献[5]，以两光伏电池串联为例说明，取无阴影光伏电池PV1的短路电流为Isc1，阴影光伏电池PV2的短路电流为Isc2。当电路电流I＞Isc2，只有PV1正常工作，输出电流为I1，超过PV2短路电流的部分从并联的二极管流过；当I＜Isc2，PV1和PV2均正常工作，输出电流为I2。

模型表达式：

式中，V1=V－f－1（Isc2）。

上述建模方法中，输出电流I2方程中的开路电压V 与分段节点即短路电流Isc2需要另行仿真计算， 从而增加了模型的复杂程度。 且随着遮挡情况的增多，计算也更为复杂，难以适用于工程实际。 在此基础上，本文提出一种改进的阴影光伏阵列建模方法。

对于单阴影阵列模型，当光伏输出电流I 小于阴影电池的短路电流Isc2时，支路上的电池均正常工作，并联的旁路二极管不起作用，输出电压为所有电池输出电压之和；反之，若输出电流大于阴影电池的短路电流Isc2，阴影电池则会成为负载，承受负压，其旁路二极管导通，其管压降为0.7 V。此时，输出电压为无阴影电池的输出电压与阴影电池承受的反压之和。

单阴影光伏阵列模型：

多阴影光伏阵列模型为：

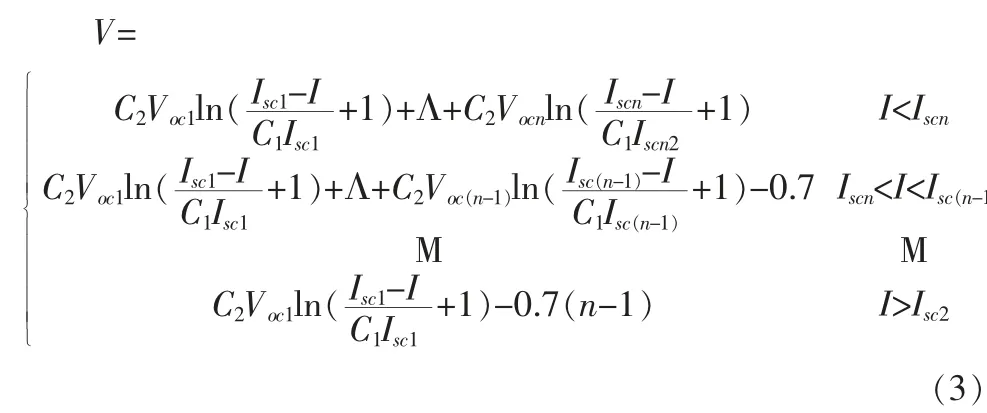
式中，Isc1，Isc2，…，Iscn、Voc1，Voc2，…，Vocn分 别 为 不 同 光 照 下的光伏电池短路电流与开路电压。

此模型避免了文献[5]中所提模型的不足，将输出电压作为输出电流的分段函数，避免了对式（1）中开路电压和短路电流的计算，从而减少计算和简化模型。 为验证其有效性，在部分遮挡条件下进行了仿真分析，结果如图1 所示。

图1 分别为阴影条件下光伏阵列机理模型输出P－V 曲线与I－V 曲线。 如图1（b）所示，局部阴影光伏阵列I－V 曲线可以看成是多段不同光照下的I－V 曲线的联合。 局域峰值之前相应的I－V 曲线段近似恒流区，曲线斜率趋近0，而局域峰值附近两端的曲线斜率则很大，相应电流变化也较大。 需要说明的是，对于光伏阵列仿真模型而言，是以ramp 函数表示电流输入，仿真时取定步长0.000 1 进行数据采样。 与斜率较大的曲线段相比，斜率趋近0 的曲线段按定步长所采集到的电压值要少的多，导致I－V 曲线与P－V 曲线段在该区域出现断续状态。

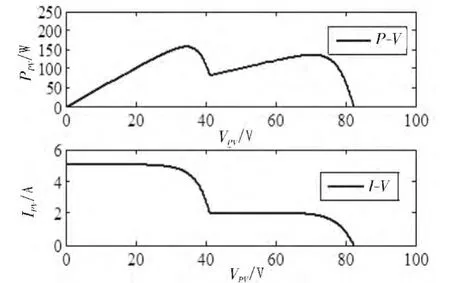
图1 阴影条件下光伏阵列输出特性曲线Fig. 1 Output characteristicof PV array under shade condition

2 基于ARX 模型的非机理模型辨识

2.1 非机理ARX 模型

为避免考虑复杂的机理模型，常用方法就是采用模型参数辨识建立相应的能够替代复杂机理模型的非机理模型。 从一组模型类中选择一个类型，按照某种准则，使之能最好的拟合所关心的实际过程的静态或动态特性，包括模型阶次辨识和参数辨识，物理系统的描述分为连续和离散两种[7]。

Matlab 自带系统辨识工具箱提供了进行系统辨识的有力工具，支持对多种模型类的辨识，包括非参数和参数等模型类。 其中，非参数模型类包括脉冲响应和频域描述等模型；参数模型类包括AR、ARX、ARMAX、BJ、 输出误差和状态空间等模型。

本文在进行系统辨识时，选择参数模型类中常用的ARX模型即自回归各态历经模型 （Auto Regressive exogenous），再采用最小二乘法对该模型中的参数进行辨识，从而建立所需非机理模型。 由于系统工具箱提供的模型是考虑了噪声影响的随机模型，随机过程中噪声可能很多，在数学模型中用一个等效的噪声代替[8]。 而ARX 模型中只存在白噪声，故其模型可表达为：

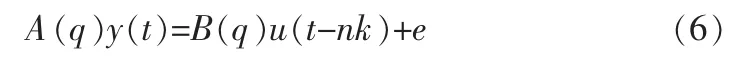
其中：

式中，na、nb、nk 分别是A（q）、B（q）的阶次与输入输出延时；y（t）为t 时刻的输出、u（t－nk）为与目前输出相关的前一刻的输入；e 为白噪声。

辨识时选择不同类型的ARX:[nanbnk]模型，通过损失函数（Loss Function）即归一化的输出预测误差平方和与最终预测误差FPE（Final Prediction Error）的大小判断辨识所得非机理模型的优劣，以获得最优辨识结果。 损失函数与FPE 表达式分别为：

式中，LF为损失函数，d 为模型表达式中需要辨识的参数个数、N 为输入电压V 的个数、Δe 为估计值与实际值的差值。其中，损失函数LF与FPE 值越小则说明辨识效果越好。

2.2 数据预处理

为了解决局域峰值之前曲线段数据短缺和不连续问题，在模型辨识前要对该区采集到的数据进行预处理， 即按照精度要求进行人为补点。

基于上述仿真分析，本文采用线性插值的方法，将局域峰值之前的I－V 曲线段按照一定要求分成若干段， 相邻点用直线连接，用直线代替I－V 曲线段。因为该区曲线斜率整体都很小且变化不大，所以可采用等距分段法，即沿着I－V 曲线的自变量V 对曲线进行等距离选取插样点。 此方法的主要优点是使间距差为常数，从而简化计算。 通过添加电压值，即可按照线性关系求出相应的电流值， 再由伏安关系得到插值点功率值。 为了减少误差，必须选取足够多的样点。

区间线性插值公式：

由式（9），得到对应插值点的功率：

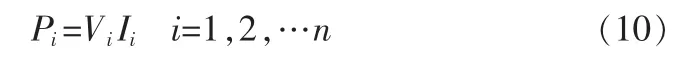
式中，Isci、Ii、Vi、Pi、ki分别表示不同遮挡下的短路电流、输出电流、输出电压、输出功率与线性插值斜率，i 表示不同的遮挡情况；其中，ki是由I－V 曲线中待插值区间相距最远的两点按照数学中两点求斜率法得到。

3 仿真结果及分析

3.1 无阴影光伏阵列模型辨识

均匀光照下， 选择标准条件下的工程用四参数模型作为辨识目标。 在MATLAB 系统辨识工具箱的模型类型中选择常用的ARX 模型，采用最小二乘法对经过预处理的输出数据进行模型辨识。改变ARX 模型的阶次获得基于不同阶次的无阴影光伏阵列的辨识模型，结果如图2 和图3 所示。

图2 基于不同ARX 模型的无阴影光伏阵列I－V 曲线Fig. 2 Output I－V curve of the non shadow PV array based on different ARX models

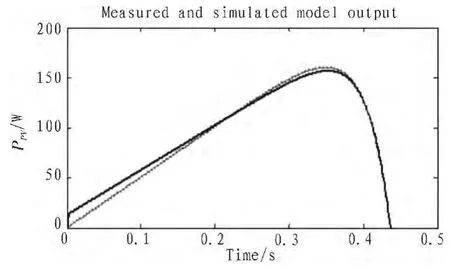
图3 基于不同ARX 模型的无阴影光伏阵列P－V 曲线Fig. 3 Output P－V curve of the non shadow PV array based on different ARX models

表1 与表2 分别为基于不同ARX 模型的独立光伏电池的I－V 曲线与P－V 曲线辨识结果。 不同阶次的ARX 模型生成精度不同的非机理模型，可通过损失函数Loss Function、最终预测误差FPE 综合判断所得模型的正确性。

结合图2～3 及表1～2 可知，无阴影条件下，光伏阵列输出I－V 曲线与P－V 曲线的辨识精度百分比均接近100%，损失函数和FPE 近似0，说明了辨识模型的正确性。 剔除精确度最低的辨识模型，将精确度最高的模型作为最终的光伏阵列非机理模型输出。

表1 基于不同ARX 模型的无阴影光伏阵列输出I-V 曲线辨识结果Tab. 1 Identification resultsof I-V curve based on different ARX models under uniform illumination

表2 基于不同ARX 模型的无阴影光伏阵列输出P-V 曲线辨识结果Tab. 2 Identification resultsof P-V curve based on different ARX models under uniform illumination

3.2 局部阴影下光伏阵列模型辨识

将上述阴影光伏阵列的机理模型在不同的遮挡情况下进行仿真：取温度T=25，单阴影条件下，无遮挡的电池光强R1=1000 W/m2，部分遮挡的电池光强R2=600 W/m2；多阴影条件下，无遮挡的电池光强R1=1000 W/m2，部分遮挡的电池光强R2=600 W/m2，深度遮挡的电池光强R3=400 W/m2。 分别将在上述条件下仿真获得的输出电压V、 电流I 及功率P 经过数据预处理即相应的线性插值后作为辨识所需的数据输入。经过与上述辨识相似的过程，辨识结果如图4－5 所示。

图4 基于不同ARX 模型的单阴影光伏阵列P－V 曲线Fig. 4 Output P－V curveof the single shadow PV array based on different ARX models

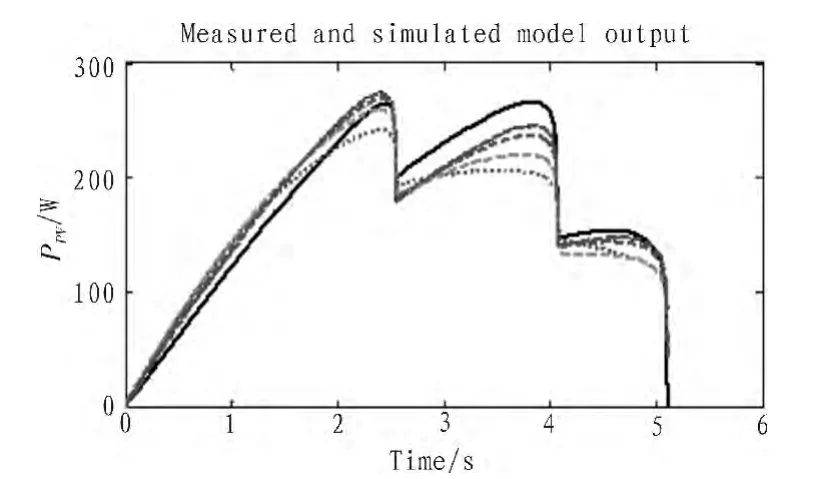
图5 基于不同ARX 模型的多阴影光伏阵列P－V 曲线Fig. 5 Output P－V curve of the multi shadow PV array basedon different ARX models

表3 与4 分别为单阴影及多阴影条件下光伏阵列P－V曲线辨识结果。 同理，在不同遮挡条件下，不同阶次的ARX模型生成精确度不同的辨识模型。

结合图4～5 与表3～4 可以看出，当光伏阵列只受到一种阴影遮挡时，由表3 知，取ARX:[1 2 1]时，即na=1、nb=2，辨 识精确度最高达76.03%， 损失函数为0.042 84，FPE 为0.042 89；当阵列受到多种阴影遮挡时，由表4 知，取ARX:[1 3 1]时，即na=1、nb=3，辨识精确度最高达79.4%，损失函数为0.049 23，FPE 为0.049 29。 所以，可以通过改变ARX 模型中A（q）与B（q）的阶次生成不同的辨识模型，将精确度最高的辨识模型作为最终的阴影光伏阵列的非机理模型输出。

表3 基于不同ARX 模型的单阴影光伏阵列输出P-V 曲线辨识结果Tab. 3 Identification resultsof output P-V curve of the single shadow PV array based on different ARX models

表4 基于不同ARX 模型的多阴影光伏阵列输出P-V 曲线辨识结果Tab. 4 Identification resultsof output P-V curve of the multi shadow PV array based on different ARX models

4 结 论

文中首先提出局部阴影下光伏阵列的机理模型，再将不同遮挡情况下的输出数据经线性插值后作为离线辨识的数据输入， 最后建立基于ARX 模型的局部阴影光伏阵列非机理模型。 结果表明，基于辨识方法获得的非机理模型能够很好的模拟光伏阵列输出，具有较高的精确度，同时大大简化了建模过程。 在工程实际应用时可采用在线辨识方法，根据实时环境变化同步获得局部阴影光伏阵列模型。 利用辨识方法建立光伏阵列非机理模型为局部阴影光伏阵列的建模提供了新的思路与方向，具有可行性。

[1] 戚军，翁国庆，章旌红. 光伏阵列多峰最大功率点分布特点研究[J]. 电力自动化设备，2014，34（3）:132－137，143.

[2] 肖景良，徐政，林崇，等. 局部阴影条件下光伏阵列的优化设计[J]. 电机工程学报，2009，20（11）:119-124.

[3] 吴小进，魏学业，于蓉蓉，等. 复杂光照环境下光伏阵列输出特性研究[J]. 中国电机工程学报，2011（31）:162-167.

[4] 陈阿莲，冯丽娜，杜春水，等. 基于支持向量机的局部阴影条件下光伏阵列建模[J].电工技术学报，2011，26（3）:140-146.

[5] 柴亚盼，金新民，童亦斌. 局部遮挡下光伏阵列的建模与仿真研究[J]. 电测与仪表，2013，576（50）:17-20，41.

[6] Ahmed K H，Finney S J，Williams B W. A Maximum Power Point Tracking Technique for Partially Shaded Photovoltaic Systems in microgrids [J]. IEEE Transactions on Industrial Electronics，2013，60（4）:1596-1606.

[7] 李立刚，张召昕，戴永寿，等. 系统辨识中最优采样间隔的确定[J]. 电子设计工程，2013，21（11）:24-26，30

[8] 周世琼，康龙云，张彦宁，等. 基于MATLAB系统辨识工具箱的风信号预测[J]. 太阳能学报， 2008，29（4）:417-421.